Il teorema di Pitagora e le sue applicazioni al quadrato
Il teorema di Pitagora è uno dei principi fondamentali della geometria e collega i lati di un triangolo rettangolo in un modo che ha affascinato matematici, scienziati e ingegneri per secoli. Questo teorema stabilisce che in un triangolo rettangolo, la somma delle aree dei quadrati costruiti sui cateti (i lati più corti del triangolo) è uguale all’area del quadrato costruito sull’ipotenusa (il lato più lungo, opposto all’angolo retto).
Nell’articolo seguente, esploreremo una varietà delle sue applicazioni pratiche, in particolare come viene utilizzato nel calcolo dell’area di quadrati. Questa esplorazione ci permetterà di comprendere meglio come questo teorema antico continui a essere un strumento essenziale in diverse aree della matematica e oltre.
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Prerequisiti per imparare le proprietà del quadrato
- Triangolo rettangolo isoscele: il quadrato e il teorema di Pitagora
- La radice quadrata di 2 e il teorema di Pitagora applicato al quadrato
- Le proprietà del quadrato e il teorema di Pitagora
Prerequisiti per imparare le proprietà del quadrato
I prerequisiti per imparare le proprietà del quadrato sono:
- teorema di Pitagora
- quadrato.
Triangolo rettangolo isoscele: il quadrato e il teorema di Pitagora

Il quadrato è un poligono regolare, con quattro angoli retti. Se tracciamo una diagonale del quadrato, lo dividiamo in due triangoli rettangoli. Come sono questi triangoli?
La diagonale divide il quadrato in due triangoli rettangoli isosceli, cioè due triangoli rettangoli che hanno i due cateti congruenti. I cateti di questi triangoli, infatti, sono uguali al lato del quadrato, quindi sono congruenti! La diagonale del quadrato è anche bisettrice degli angoli: gli angoli adiacenti all’ipotenusa del triangolo rettangolo isoscele sono congruenti e misurano 45°.
Il triangolo rettangolo isoscele, quindi, ha due angoli di 45° e un angolo di 90°. Il triangolo rettangolo isoscele è la metà di un quadrato! Come la squadretta che utilizzi per il disegno tecnico! La più piccola è un triangolo rettangolo con due angoli da 45°.
La radice quadrata di 2 e il teorema di Pitagora applicato al quadrato
Prendiamo un quadrato con lato di £$ 1 \text{ cm} $£. Tracciamo la sua diagonale. Quanto misura?
Abbiamo appena imparato che la diagonale divide il quadrato in due triangoli rettangoli isosceli. Quindi applichiamo il teorema di Pitagora per trovare la sua misura. La diagonale del quadrato corrisponde all’ipotenusa dei triangoli, quindi per trovare la sua misura dobbiamo sommare i quadrati dei due cateti di £$ 1 \text{ cm} $£ e calcolare la radice quadrata del risultato:
$$ \text{diagonale} = \sqrt{1^2\text{ cm}^2+ 1^2\text{ cm}^2} = \sqrt{2 \text{ cm}^2} = \sqrt 2 \text{ cm} $$
La diagonale di un quadrato con il lato di £$ 1 \text{ cm} $£ misura £$ \sqrt 2 \text{ cm} $£.
Grazie a questa applicazione del teorema di Pitagora, abbiamo scoperto questo “strano" numero: £$ \sqrt 2 $£ è la misura dell’ipotenusa di un triangolo rettangolo isoscele con cateti unitari, o meglio ancora è la misura della diagonale di un quadrato con il lato unitario. Il calcolo che abbiamo fatto, a noi non sembra così sconvolgente, ma in verità questa scoperta ha messo in crisi la matematica greca. I pitagorici cercavano di scrivere tutto sotto forma di numero intero, o di rapporto tra numeri interi. Non è così facile trovare un numero il cui quadrato sia uguale a £$ \sqrt 2 $£ e nemmeno due numeri il cui rapporto dia come risultato £$ \sqrt 2 $£. Si tratta infatti di un numero irrazionale!
Le proprietà del quadrato e il teorema di Pitagora
Formule quadrato
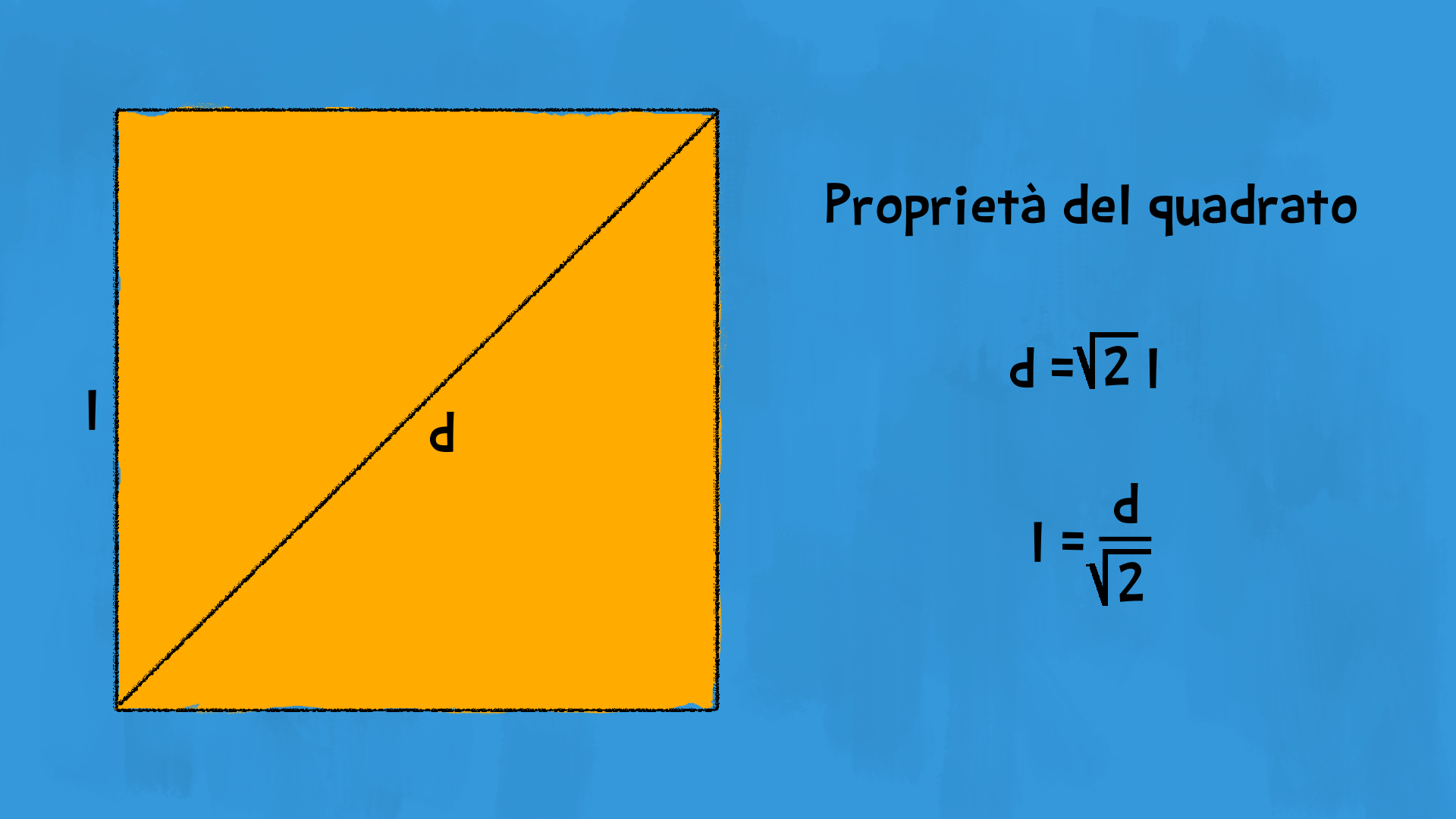
Esercizio svolto: quadrato
Grazie al teorema di Pitagora, abbiamo potuto scoprire e studiare un numero molto particolare: £$ \sqrt 2 $£. Abbiamo potuto scoprire la relazione tra un lato di un quadrato e la sua diagonale.
In un quadrato di lato £$ \ell $£:
- la diagonale è uguale alla lunghezza del lato moltiplicata per £$ \sqrt 2 $£, cioè £$ d = \ell \cdot \sqrt 2 $£;
- il lato è uguale alla lunghezza della diagonale divisa per £$ \sqrt 2 $£, cioè £$ \ell = \frac{d}{\sqrt 2} $£
Quando ci troviamo davanti ad un quadrato, quindi, possiamo ricordarci di queste proprietà senza dover applicare il teorema di Pitagora per calcolare la lunghezza della diagonale!
