Le dimensioni della Terra: quali sono e come si calcolano
Da secoli, la forma della Terra ha affascinato, confuso e ispirato umanità, artisti, filosofi e scienziati. Una volta ritenuta piatta, un tavolo su cui si dispiegavano mari e continenti, la nostra comprensione del pianeta è radicalmente cambiata grazie alle scoperte e alle ricerche incessanti degli studiosi. Oggi sappiamo con certezza che la Terra è rotonda e non piatta, come si credeva in passato. Più precisamente è un geoide, una forma leggermente schiacciata ai poli e rigonfia all’equatore. Ma come siamo arrivati a questa conclusione? E come misuriamo esattamente la grandezza e la forma del nostro pianeta?
Le dimensioni della Terra e la sua forma sono state determinate attraverso metodi sofisticati, combinando osservazioni astronomiche, misurazioni geodetiche e tecnologie satellitari nei tempi più recenti. Calcolare la circonferenza, il diametro, l’area di superficie e il volume può sembrare difficile, ma una volta imparato quali sono le caratteristiche della forma della Terra è in realtà molto semplice!
Nel corso di questo articolo esploreremo la forma rotonda della Terra, le sue dimensioni esatte e i metodi utilizzati per calcolarle. Pronti? Cominciamo!
- La forma della Terra: cos'è un geoide
- Caratteristiche fisiche della Terra: massa, densità, temperatura
La forma della Terra: cos’è un geoide
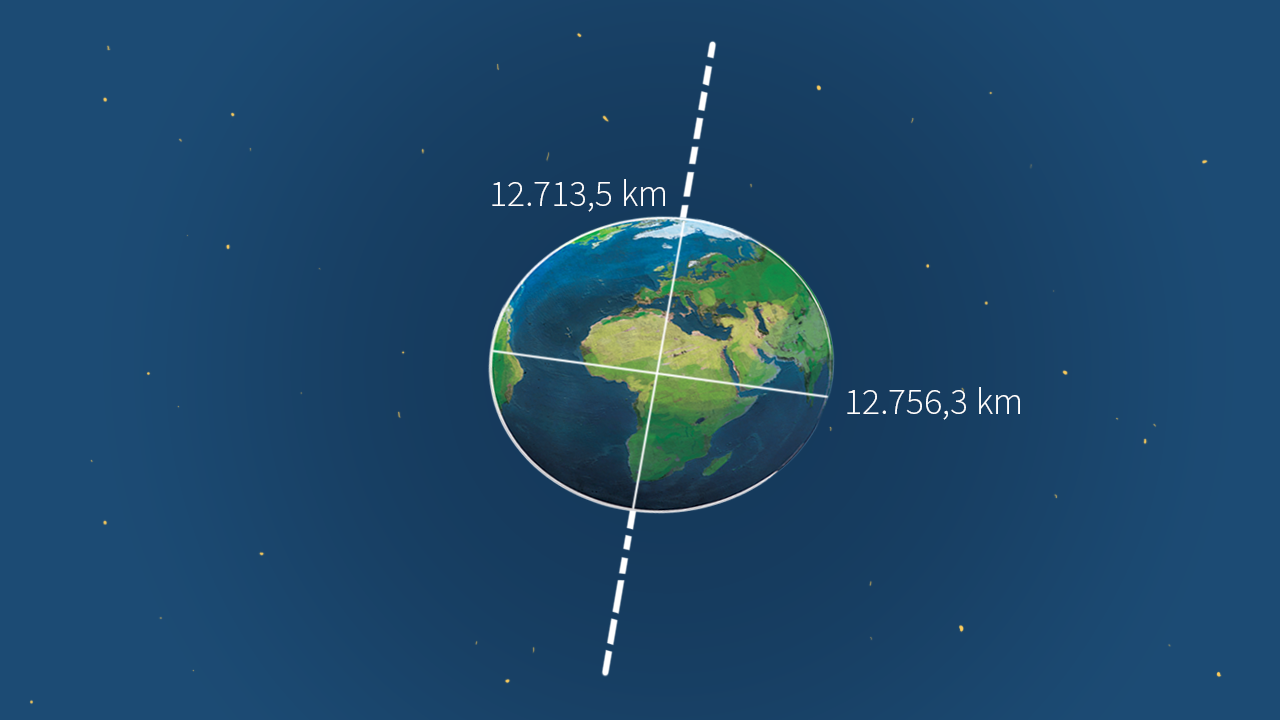
La forma della Terra non è quella di una sfera perfetta: a causa della rotazione attorno al proprio asse, infatti, la Terra non è rotonda, ma è leggermente schiacciata ai poli e più prominente all’equatore (rigonfiamento equatoriale), un po’ come un mandarancio.
Più precisamente si dice che è un geoide, solido che, per definizione, ha la forma della Terra (quindi potremmo dire che la Terra ha la forma di se stessa!). Un geoide è molto simile ad un ellissoide, ossia un solido geometrico generato dalla rotazione di un’ellisse attorno al proprio asse minore; rispetto a questo ellissoide di riferimento, il geoide si discosta al massimo di 100 metri.
La principale conseguenza della forma della Terra è che il diametro equatoriale £$ (12 \, 756{,}3 \text{ km}) $£ è leggermente maggiore di quello polare £$ (12 \, 713{,}5 \text{ km}) $£.
Il diametro medio dell’ellissoide di riferimento corrisponde, in maniera approssimativa, al rapporto tra la circonferenza terrestre lungo un meridiano e il pi greco, ossia £$ 40 \, 009 \text{ km/}\pi $£.
Eratostene, nel £$ 200 \text{ a.C.} $£, con gli strumenti a sua disposizione arrivò a calcolare un valore della circonferenza terrestre molto simile, £$ 40 \, 500 \text{ km} $£.
Caratteristiche fisiche della Terra: massa, densità, temperatura
La massa della Terra è circa di £$ 5{,}98 \times 10^{24} \text{ kg} $£, ossia quasi £$ 6000 $£ trilioni di tonnellate! (Ricorda la differenza tra peso e massa!).
Questo valore non è costante, ma varia nel tempo, aumentando di circa £$ 10^7 \text{ kg/anno} $£ (cioè £$ 10 \, 000 \, 000 $£ di chilogrammi, equivalenti a £$ 10 \, 000 $£ tonnellate ogni anno) a causa della caduta sulla superficie del pianeta di materiale cosmico.
Il volume è pari a £$ 1{,}083 \times 10^{21} \text{ m}^3 $£, equivalente al volume di una sfera con raggio £$ r = 6 \, 371 \text{ km} $£; allo stesso modo, la sua superficie è circa £$ 5{,}095 \times 10^{14} \text{ m}^2 $£, pari a oltre £$ 100 $£ miliardi di campi da calcio.
La densità media della Terra, data dal rapporto tra la sua massa e il suo volume, è di £$ 5 \, 514 \text{ kg/m}^3 $£ (ovvero circa £$ 5{,}5 \text{ g/cm}^3 $£) e questo la rende il pianeta più denso del Sistema Solare. Per fare un paragone, Saturno ha una densità di soli £$ 687 \text{ kg/m}^3 $£, inferiore a quella dell’acqua: se esistesse un oceano abbastanza grande da contenerlo, Saturno galleggerebbe.
La densità terrestre però non è un parametro costante, ma cresce all’aumentare della profondità: partendo dai £$ 2{,}2 – 2{,}9 \text{ g/cm}^3 $£ nella crosta terrestre e passando per i £$ 3 – 5{,}6 \text{ g/cm}^3 $£ nel mantello, si raggiungono nel nucleo valori compresi tra i £$ 9 $£ e i £$ 13{,}5 \text{ g/cm}^3 $£. Un metro cubo di roccia del nucleo pesa quanto £$ 3 $£ elefanti adulti!
La temperatura all’interno della Terra aumenta di circa £$ 25 ^°C $£ ogni chilometro di profondità nella crosta, mentre al di sotto (mantello e nucleo) cresce più lentamente, circa £$ 0{,}7 ^°C – 0{,}8 ^°C $£ per chilometro. Nel nucleo interno raggiunge i £$ 5 \, 270 K $£ (circa £$ 5 \, 000 ^°C $£), molto vicina a quella della superficie del Sole £$ (5 \, 778 K) $£.
Anche la pressione (detta litostatica, perché dovuta al peso delle rocce sovrastanti) aumenta al crescere della profondità, per raggiungere il valore di £$ 3\, 600 \text{ kbar} $£ nel nucleo interno, ossia £$ 3 \, 500 \, 000 $£ volte la pressione atmosferica.
