Formulario di fisica: la forza elettrostatica
L’Universo, in tutta la sua complessità, è guidato da forze invisibili che determinano la natura dei fenomeni che osserviamo quotidianamente. Una di queste forze fondamentali è la forza elettrostatica: nonostante la sua pervasività e la sua importanza in innumerevoli applicazioni e tecnologie, la comprensione di tale forza può presentare sfide per chi si avvicina per la prima volta alle leggi che la governano.
La forza elettrostatica emerge dalla interazione tra cariche elettriche. Questo tipo di interazione è responsabile di molte delle proprietà dei materiali che ci circondano, dall’adesione, alla repulsione, fino alla conduzione elettrica in metalli e semiconduttori. Le leggi che la descrivono sono state formulate secoli fa, eppure restano fondamentali e inalterate.
Scopriamo insieme quali sono le formule principali che coinvolgono gli studi dello scienziato Coulomb!
La legge di Coulomb per due cariche nel vuoto
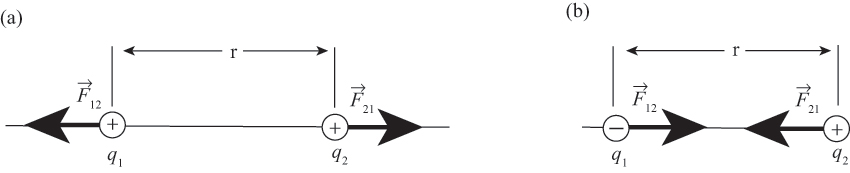
L’intensità dell’interazione elettrica tra due cariche elettriche puntiformi £$q_1$£ e £$q_2$£ poste nel vuoto a distanza £$r_{12}$£, è data dalla legge di Coulomb: $$\vec F= \frac{1}{4\pi \epsilon_0} \frac{q_1q_2}{(r_{12})^2} \, \hat{r}. $$ La forza è diretta lungo la retta congiungente £$q_1$£ e £$q_2$£ ed è attrattiva quando le cariche hanno segno opposto o repulsiva quando le cariche hanno lo stesso segno.
£$\epsilon_0 = 8,85 \cdot 10^{-12} \, \frac{C^2}{N\,m^2}$£ è la costante dielettrica del vuoto; spesso si pone £$\frac{1}{4\pi\epsilon_0}=k$£, con £$k=8,99\cdot 10^9 \frac{N \,m^2}{C^2}$£.
La forza di Coulomb è conservativa.
La legge di Coulomb per due cariche in un mezzo
Se le due cariche sono poste in un mezzo, la forza £$F$£ con cui interagiscono elettrostaticamente è minore in modulo rispetto alla loro interazione nel vuoto £$F_0$£. Il rapporto tra £$F_0$£ e £$F$£ è pari alla costante dielettrica relativa £$\epsilon_r$£, che è un coefficiente caratteristico del materiale: £$\epsilon_r= \frac{F_0}{F}$£.
La legge di Coulomb diventa:
$$\vec F= \frac{1}{4\pi \epsilon_0 \epsilon_r} \frac{q_1q_2}{(r_{12})^2} \, \hat{r} $$
dove si pone £$\epsilon=\epsilon_0\epsilon_r$£ costante dielettrica assoluta.
Il legame tra l’elettrostatica e la legge di Coulomb
L’elettrostatica è un pilastro fondamentale della fisica che affronta il comportamento delle cariche elettriche in assenza di movimento, ovvero quando sono in uno stato statico. Una delle leggi cardine che governano questo comportamento è la legge di Coulomb, fondamentale per intuire come le cariche interagiscono tra di loro.
Questa legge fu formulata nel 18° secolo dal fisico francese Charles-Augustin de Coulomb attraverso un esperimento con una bilancia a torsione. Essa afferma che la forza elettrostatica tra due cariche puntiformi è direttamente proporzionale al prodotto delle cariche stesse e inversamente proporzionale al quadrato della distanza che le separa. In termini più semplici, questo significa che cariche dello stesso tipo si respingono, mentre cariche di tipo opposto si attraggono.
Questa legge ha profonde implicazioni. Per esempio, ha aiutato gli scienziati a capire perché gli atomi si combinano per formare molecole: gli elettroni (con carica negativa) orbitano intorno al nucleo (con carica positiva) a causa di questa forza di attrazione elettrostatica.
La legge di Coulomb è anche strettamente legata alle equazioni di Maxwell, che sono fondamentali nella teoria dell’elettromagnetismo. Le applicazioni pratiche della comprensione delle forze elettrostatiche sono vastissime, dalla spiegazione del funzionamento di un semplice pettine che attira pezzetti di carta, fino alle tecnologie più avanzate come le memorie di computer e i dispositivi di immagazzinamento dei dati.
