Sezioni coniche: definizione e applicazione
La geometria analitica è quel ramo della matematica in cui si uniscono l’algebra e la geometria, studiando quelle curve che chiamiamo coniche. La parabola, la circonferenza, l’ellisse e l’iperbole si chiamano in generale coniche perché sono ottenute da diverse sezioni di un cono.
Le sezioni coniche si ottengono tagliando un cono con un piano. A seconda dell’intersezione tra un cono a due falde ed un piano nello spazio otteniamo diversi tipi di coniche: impara come ricavare la parabola, l’ellisse, la circonferenza e l’iperbole e scopri perché vengono chiamate anche coniche.
Che cos’è una conica
Le coniche, o sezioni coniche, sono figure geometriche che emergono come intersezioni di un piano con un cono a doppia falda. La forma della sezione conica risultante dipende dall’angolo e dalla direzione in cui il piano taglia il cono. Queste curve sono fondamentali in matematica e hanno numerose applicazioni in fisica, ingegneria e altre scienze.
L’aggettivo coniche ci suggerisce di considerare un cono: dobbiamo però considerare il cono a due falde cioè il solido ottenuto dalla rotazione di una retta inclinata di un certo angolo!
Come ottenere le coniche
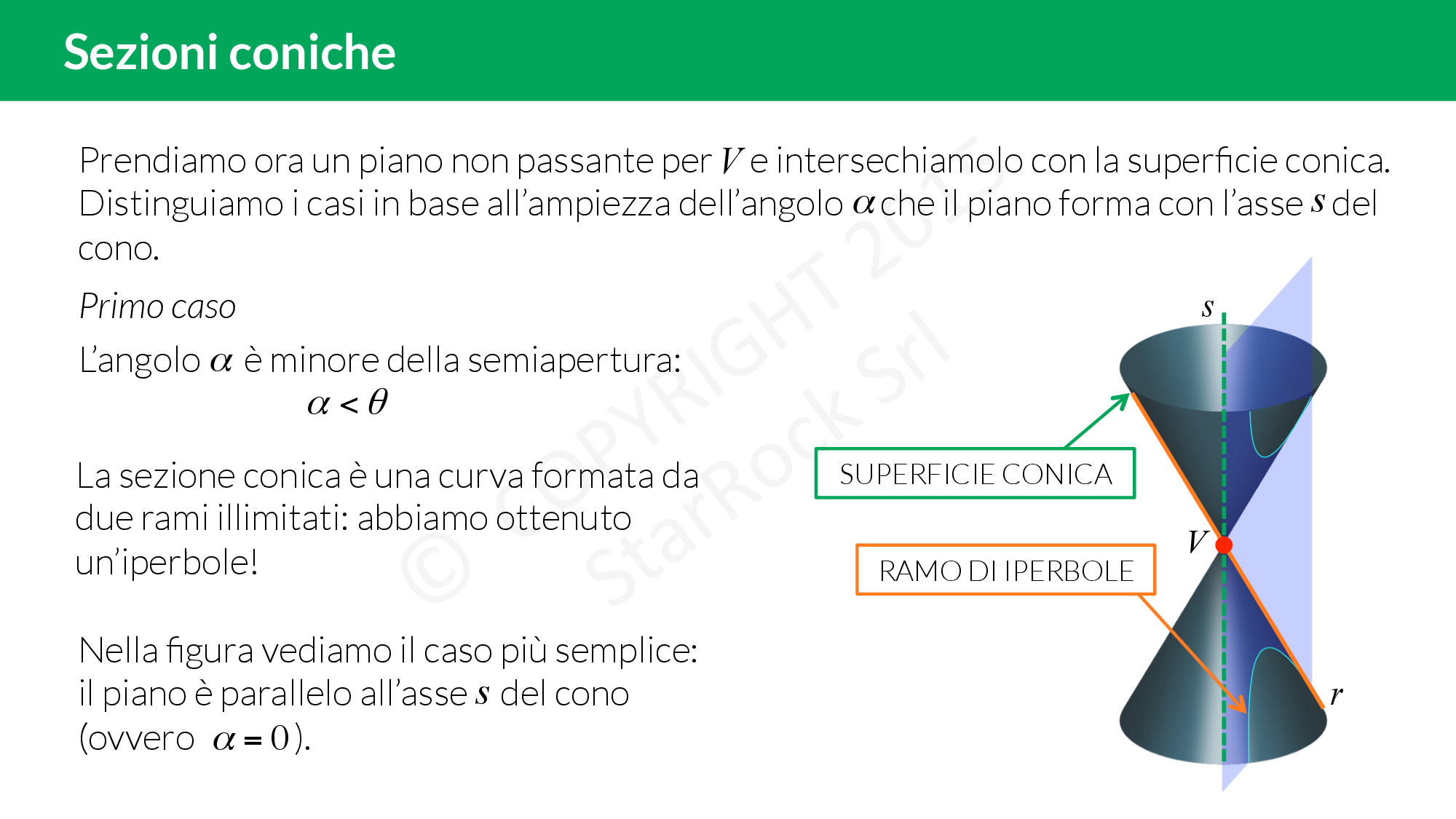
Primo caso
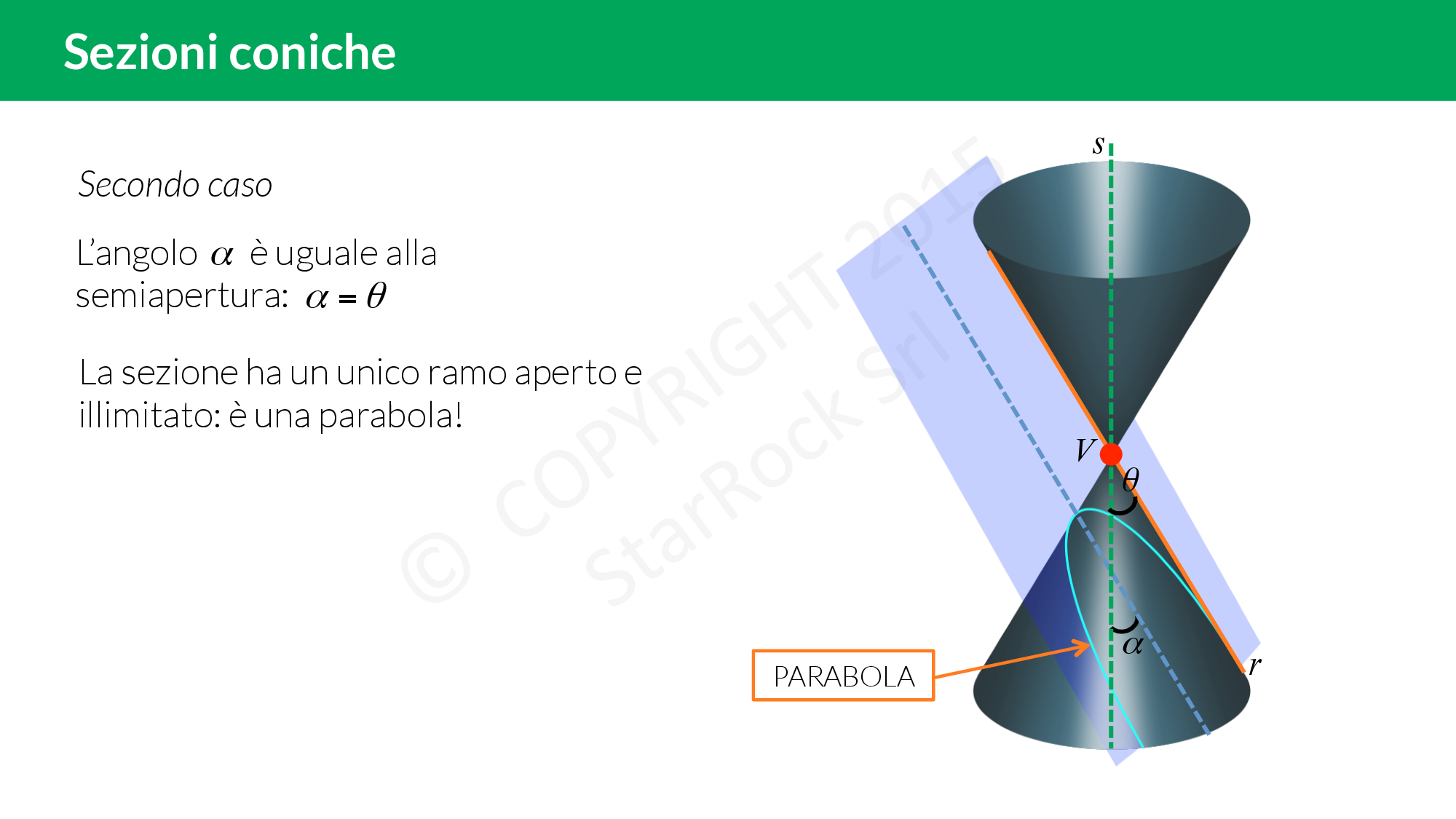
Secondo caso
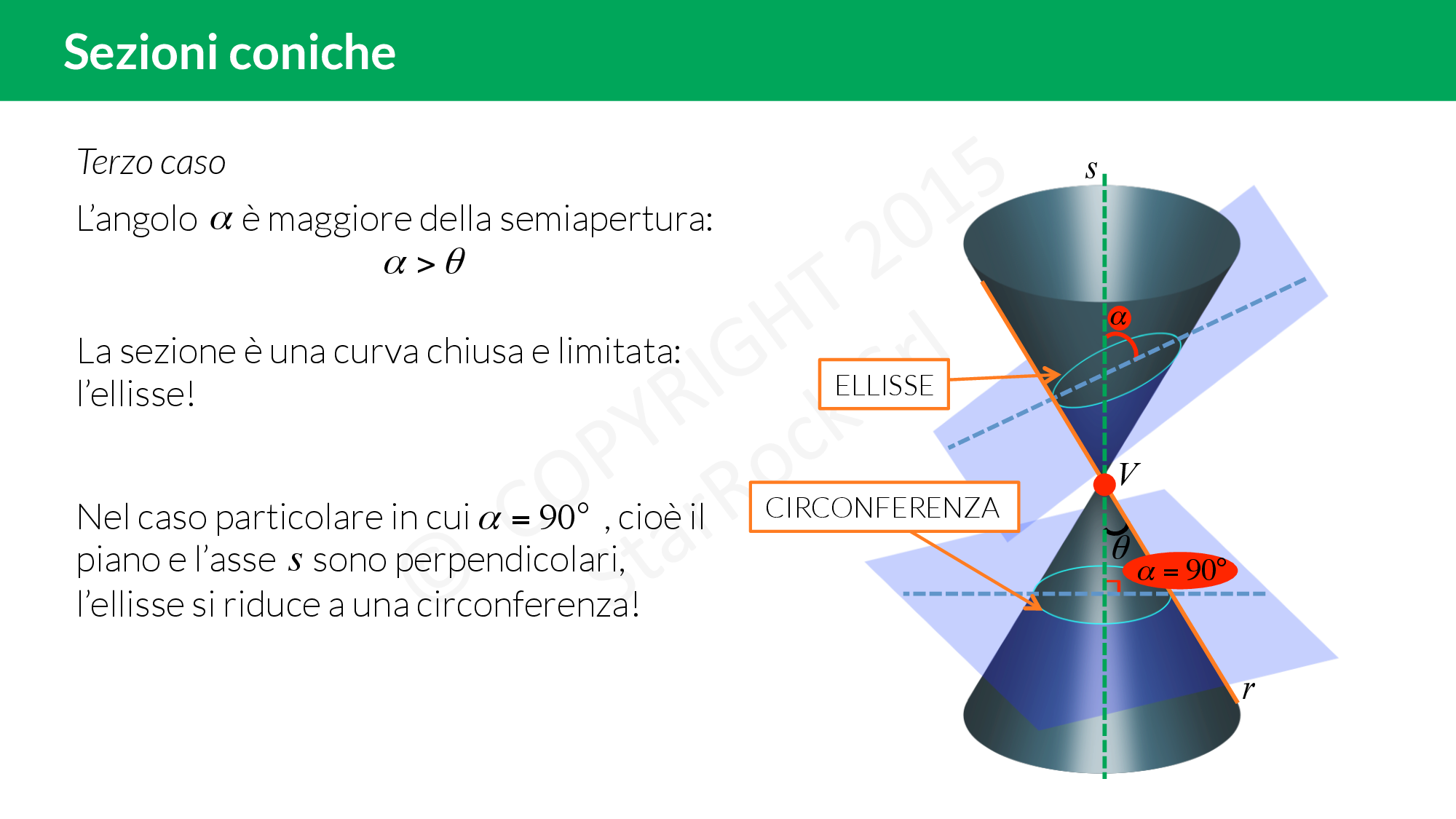
Terzo caso
Nello spazio analizziamo le sezioni di un cono con un piano: a seconda di come è messo il piano rispetto al cono, otteniamo figure diverse:
- il piano è parallelo all’asse del cono: la sezione è un’iperbole;
- l’angolo fra il piano e l’asse del cono è uguale a quello fra l’asse del cono ed una delle rette generatrici: la sezione è una parabola;
- il piano forma con l’asse un angolo maggiore di quello tra la generatrice e l’asse: la sezione è un’ellisse;
- il piano è perpendicolare all’asse del cono: la sezione è una circonferenza;
Coniche degeneri
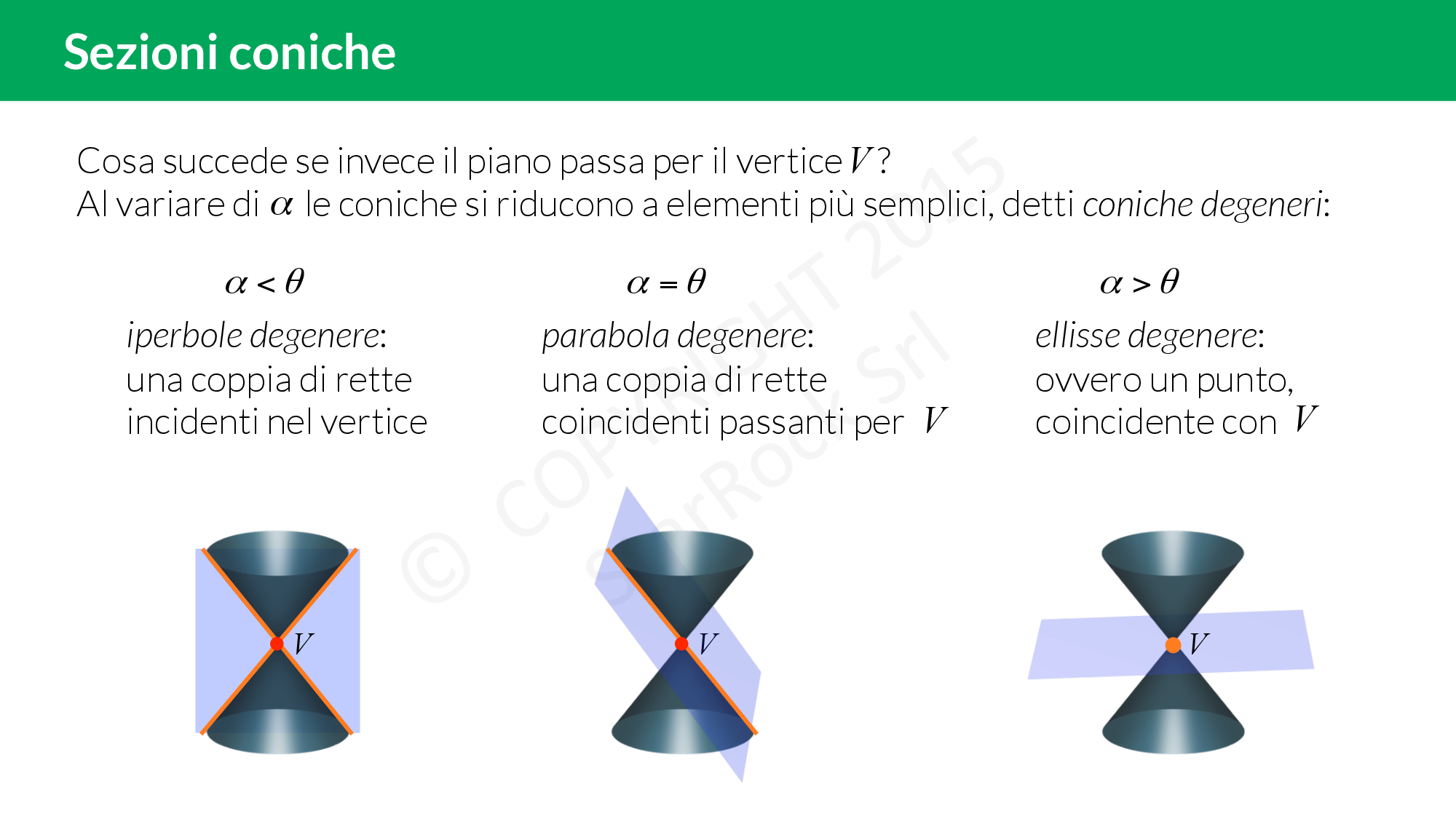
Le coniche degeneri sono forme particolari delle sezioni coniche che si ottengono sotto condizioni specifiche quando il piano taglia un cono a doppia falda. A differenza delle coniche standard come ellissi, parabole e iperboli, le coniche degeneri non formano curve chiuse o aperte continue, ma piuttosto si riducono a figure più semplici come:
- Punto: Una conica può degenerare in un singolo punto quando il piano di taglio passa esattamente per il vertice del cono. In questo caso, tutte le sezioni del cono in quel punto si riducono a un punto isolato. Questo è un esempio di ellisse degenere.
- Linea: Se il piano taglia il cono parallelamente all’asse del cono, la sezione conica risultante può essere una linea retta, dunque una parabola degenere.
- Coppia di linee intersecanti: Questa forma degenerata si verifica quando il piano taglia il cono in modo tale da intersecare entrambe le falde lungo linee che si incrociano. In pratica, il risultato è due rette che si intersecano in un punto, il vertice del cono, cioè l’iperbole degenere.




