Sistemi parametrici con l'iperbole: risoluzione
Hai visto come risolvere i sistemi parametrici in cui la conica “protagonista" era la circonferenza, la parabola e l’ellisse. Chi manca all’appello? L’iperbole!
Adesso scopri come si risolvono i sistemi parametrici con l’iperbole. Non spaventarti, il metodo è sempre uguale, cambia solo la conica:
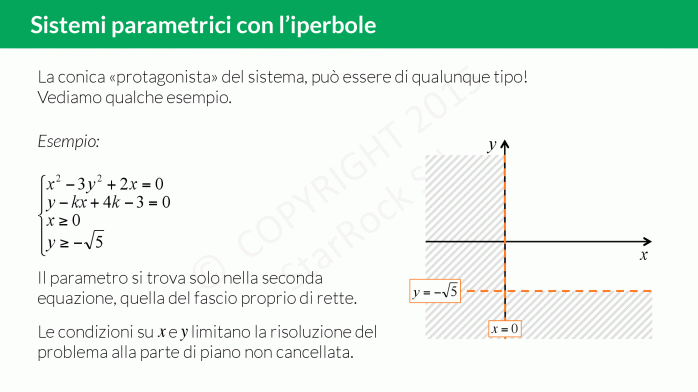
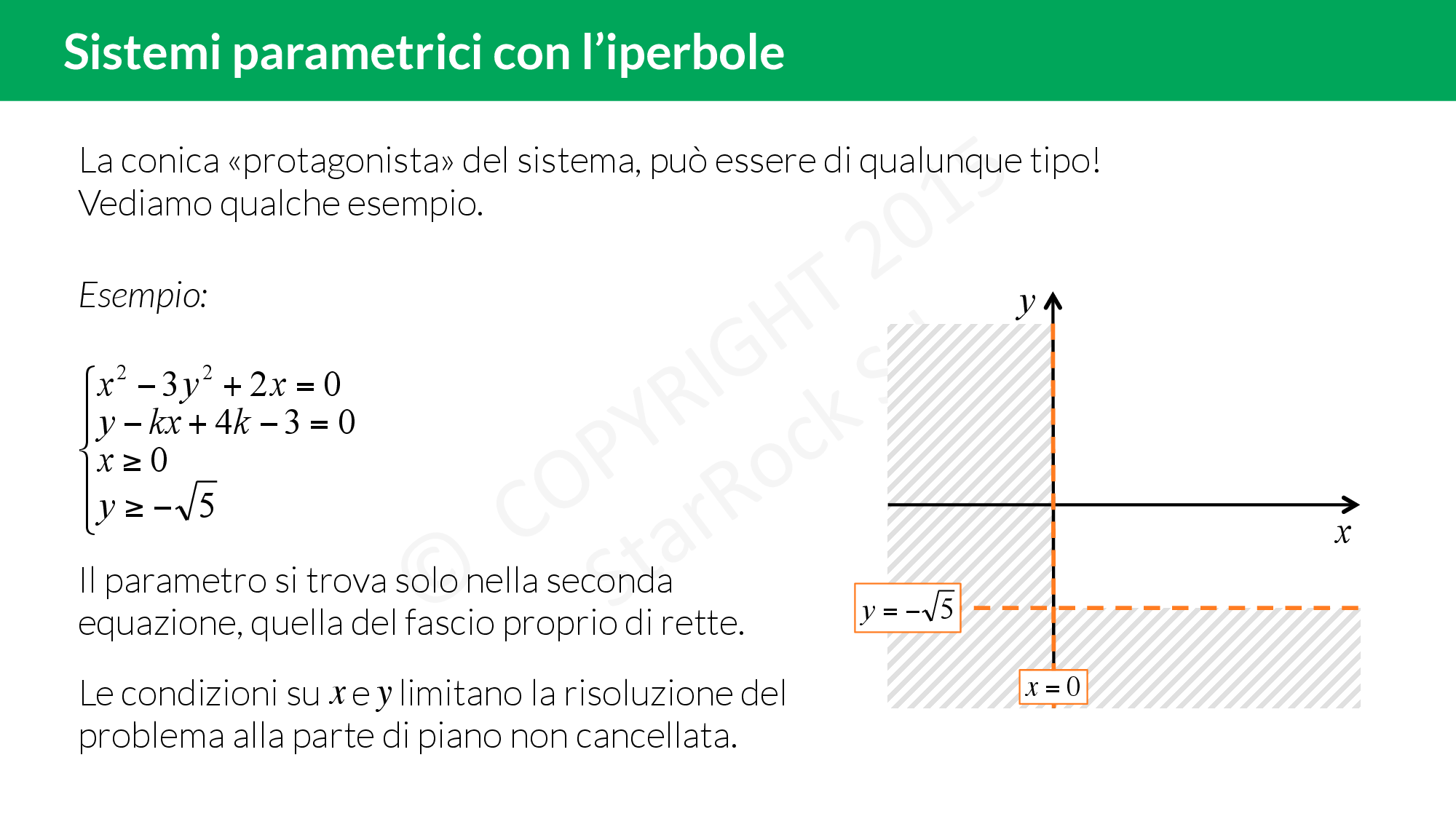
- per prima cosa imponi le limitazioni (se ce ne sono nel sistema) su £$x$£ e £$y$£ così da “cancellare" delle parti di piano;
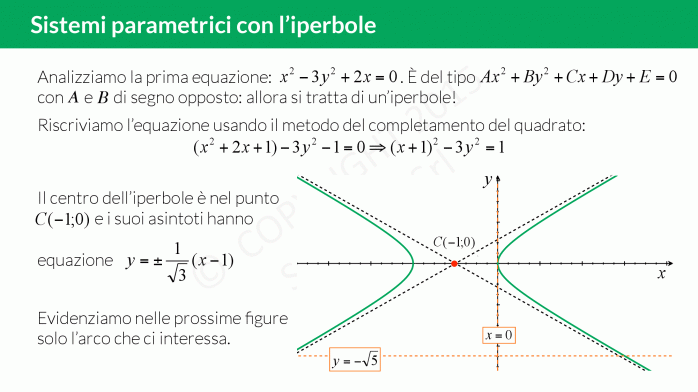
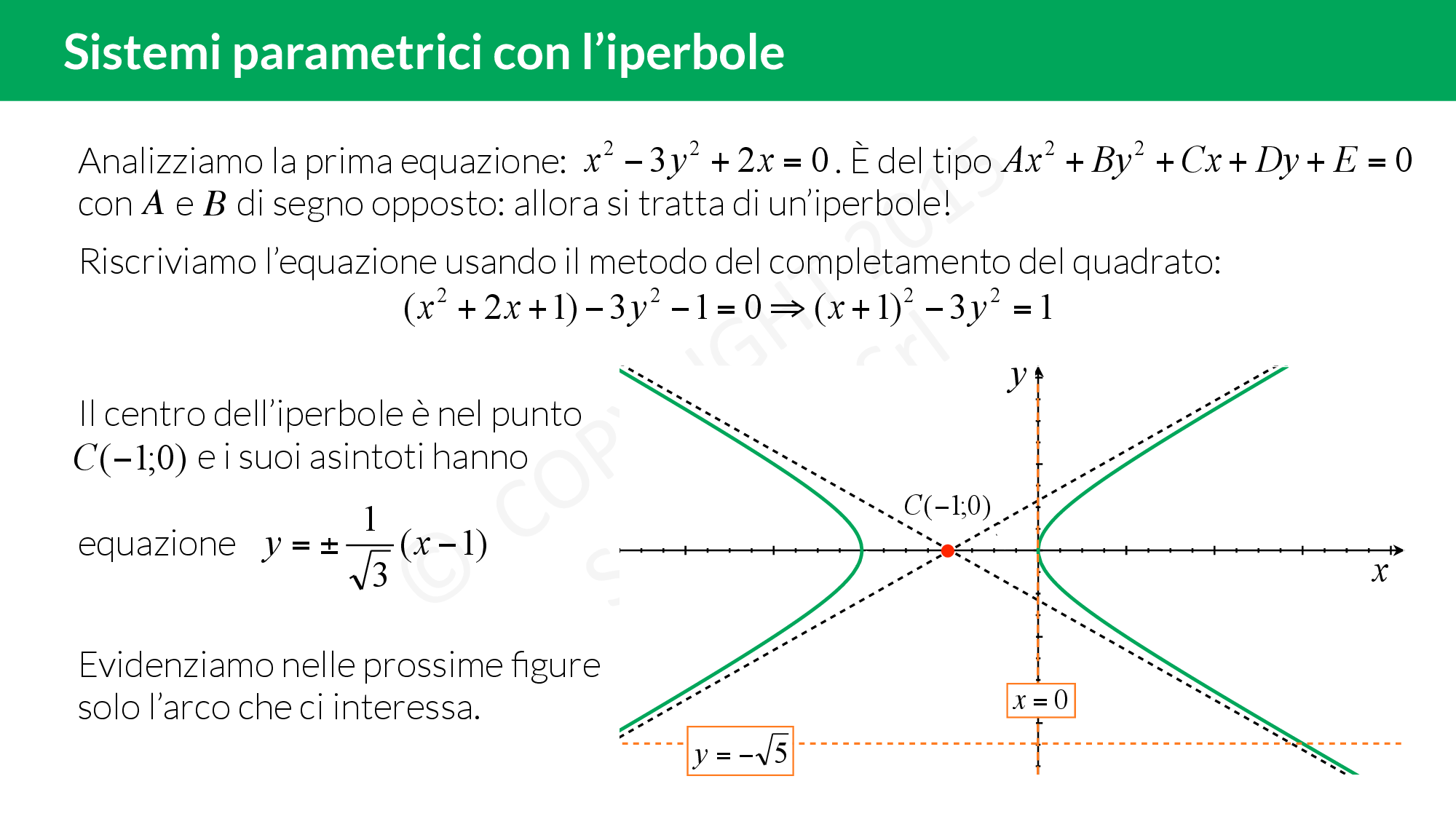
- traccia il grafico delle funzioni senza il parametro;
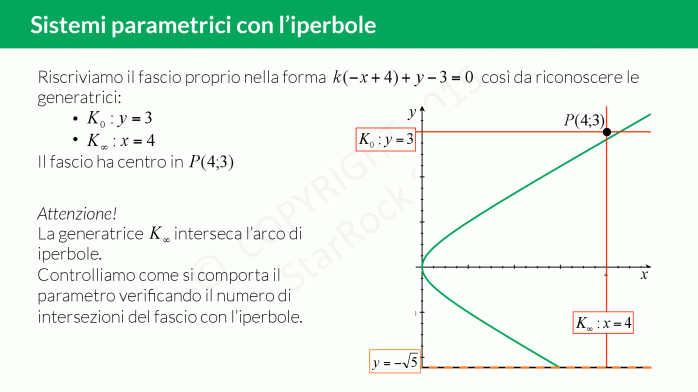
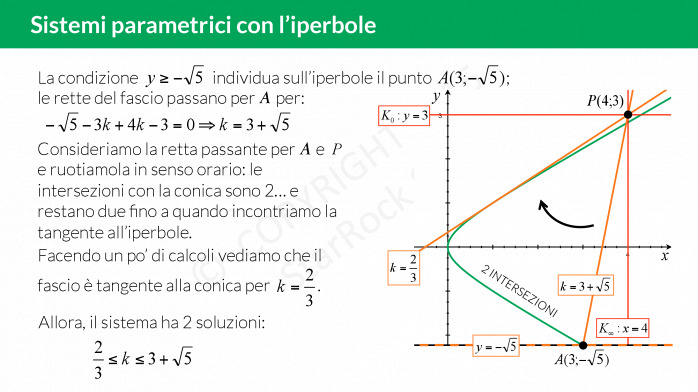
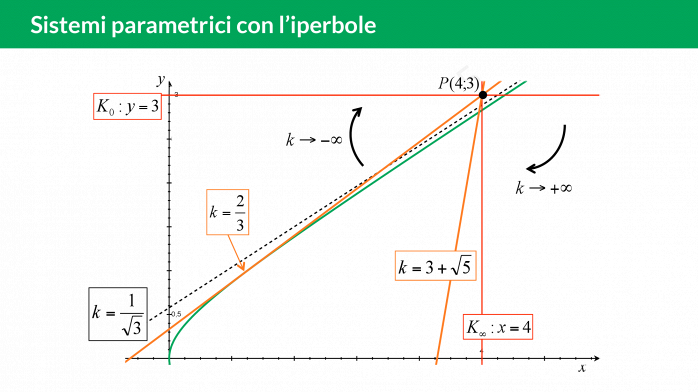
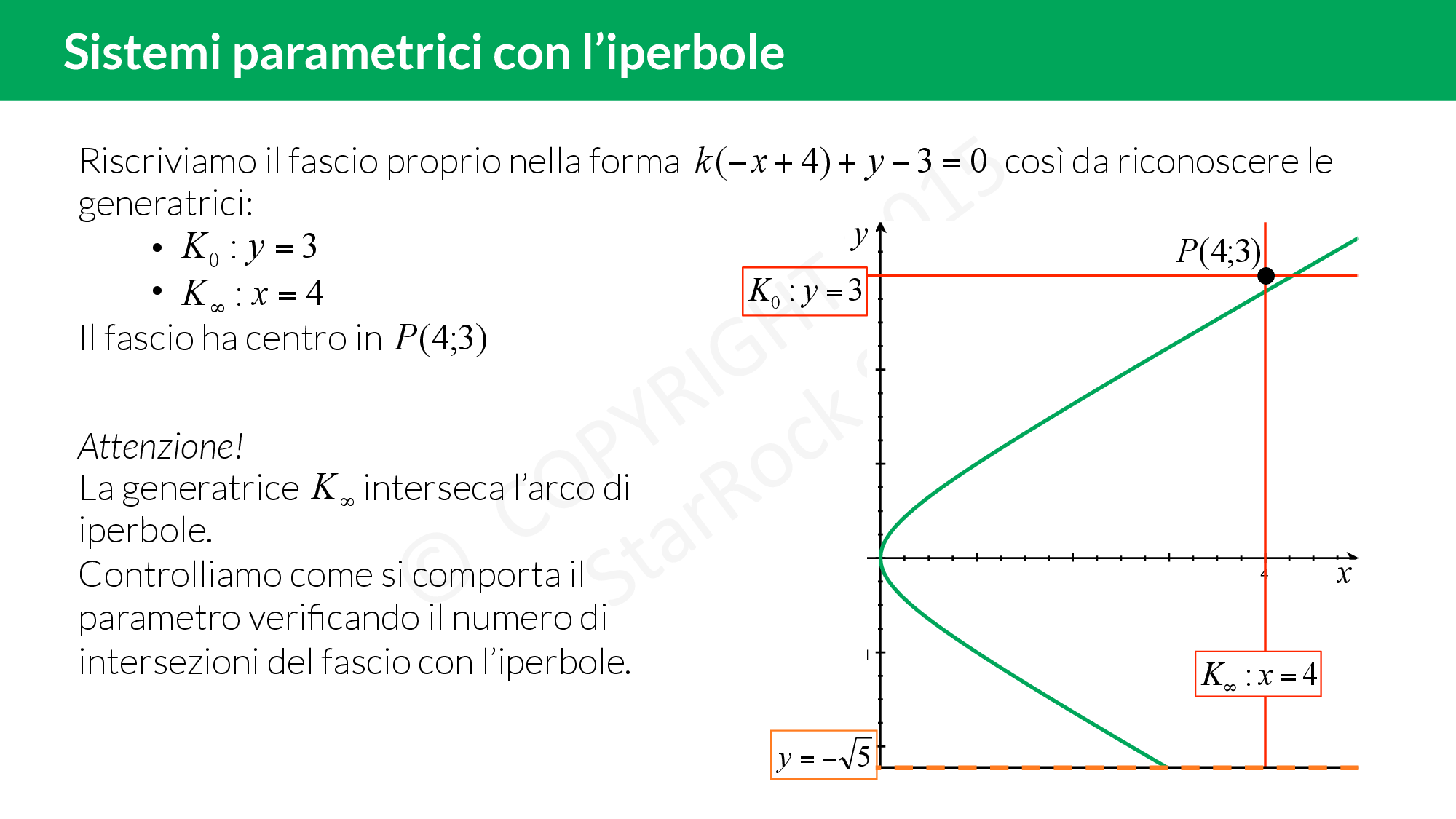
- infine fai variare il parametro della funzione mancante per scoprire le intersezioni con le altre curve.
I sistemi parametrici possono essere utilizzati per descrivere e risolvere problemi complessi che coinvolgono l’iperbole, una delle curve coniche più utili in matematica. L’iperbole, con la sua distinta forma a doppio arco che si estende all’infinito, trova applicazione in molti campi, dalla fisica all’ingegneria, e la sua rappresentazione parametrica offre un metodo potente e flessibile per trattare questi problemi con precisione e efficacia.
- Cos'è l'iperbole
- Sistemi parametrici con l'iperbole
- Interrogazione su sistemi parametrici con l'iperbole
- Sfida sui sistemi parametrici con l'iperbole
Cos’è l’iperbole
L’iperbole è una delle curve coniche ottenute dall’intersezione di un cono con un piano che taglia entrambi i coni della doppia superficie conica, ma non interseca la base. Questa particolare figura geometrica si caratterizza per avere due rami simmetrici che si estendono all’infinito, mai incontrandosi.
Un sistema parametrico in matematica è un metodo per esprimere un insieme di quantità come funzioni esplicite di una o più variabili indipendenti, note come parametri. Nei sistemi di equazioni, l’uso di parametri può semplificare la rappresentazione di curve e superfici consentendo la descrizione di queste figure nello spazio mediante equazioni dipendenti da questi parametri.
Sistemi parametrici con l’iperbole
Sistemi parametrici con l'iperbole - Galleria
Quando affronti il calcolo di un sistema parametrico può capitarti che una delle equazioni sia un’iperbole!
La rappresentazione parametrica dell’iperbole offre diversi vantaggi:
- Semplificazione delle equazioni: La forma parametrica può semplificare l’integrazione o la derivazione rispetto alle equazioni cartesiane, particolarmente utile in problemi di ottica e meccanica.
- Analisi matematica: In matematica, permette di esplorare più facilmente le proprietà intrinseche dell’iperbole, come asintoti, tangenti e normali in vari punti, che possono essere più complesse da calcolare in forma cartesiana.
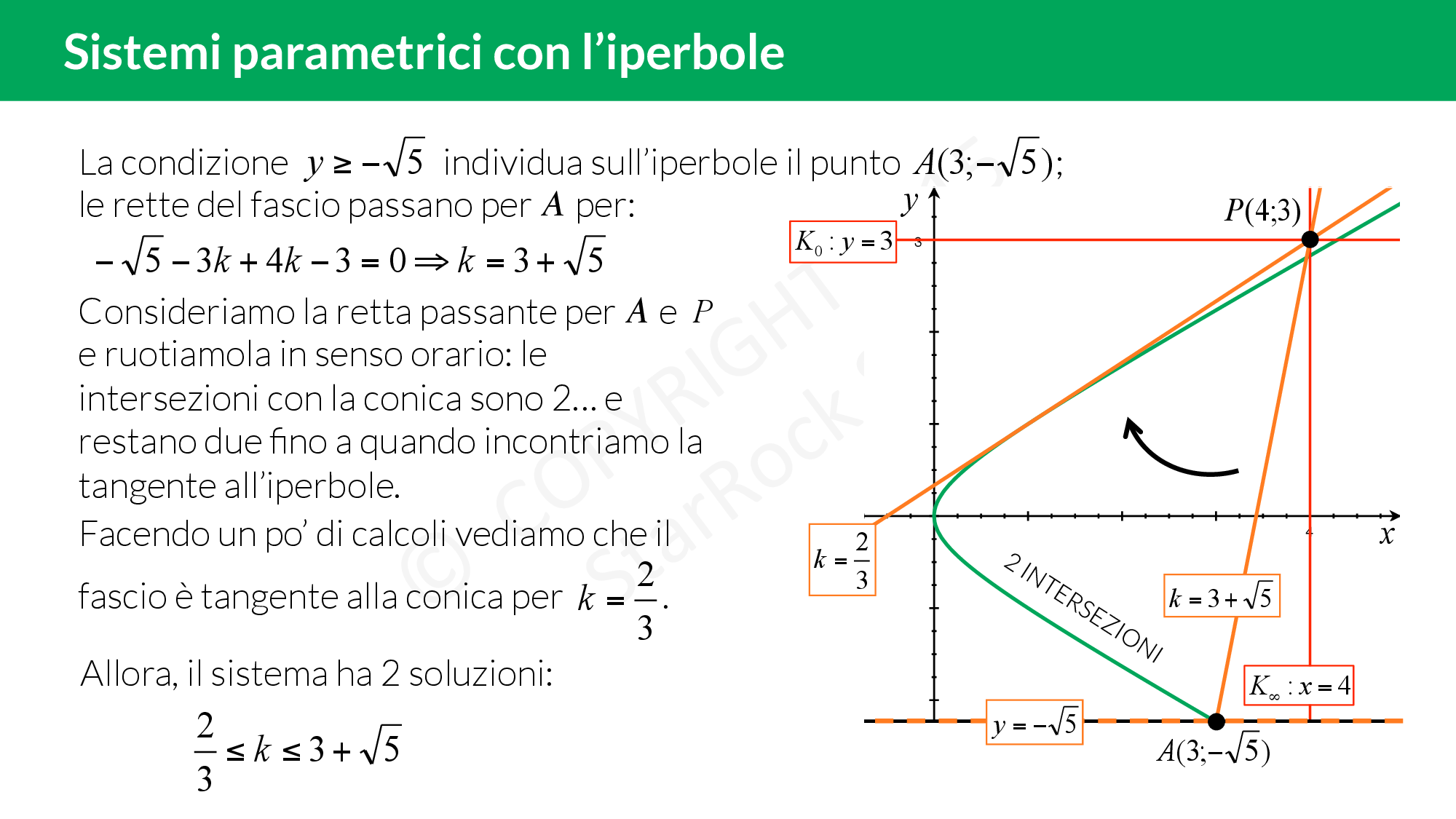
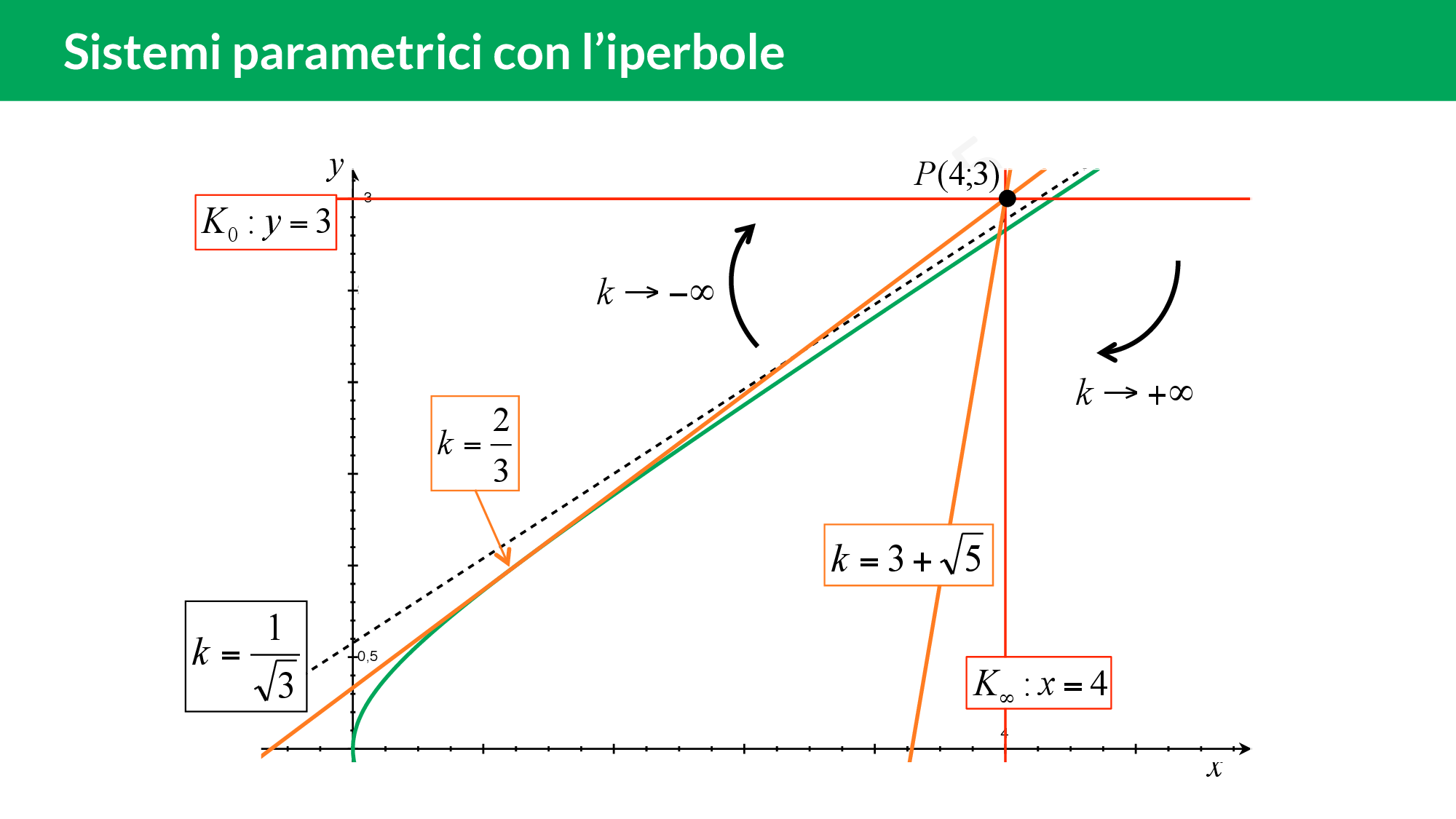
Qui trovi un esercizio spiegato passo per passo: imponi per prima cosa le limitazioni su £$x$£ e £$y$£, disegna l’iperbole e poi verifica quante intersezioni ha quest’ultima con il fascio di rette!
Interrogazione su sistemi parametrici con l’iperbole
Prova a risolvere i sistemi parametrici con l’iperbole che trovi nell’interrogazione: magari uno di questi due esercizi ti capiterà nella prossima verifica!
Sfida sui sistemi parametrici con l’iperbole
Sfida:
Sistemi parametrici con l'iperbole - Galleria
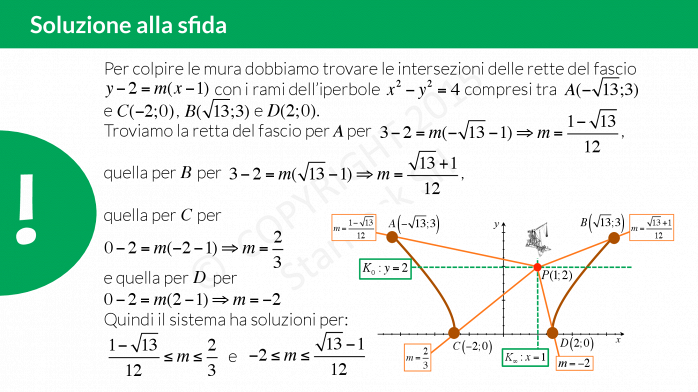
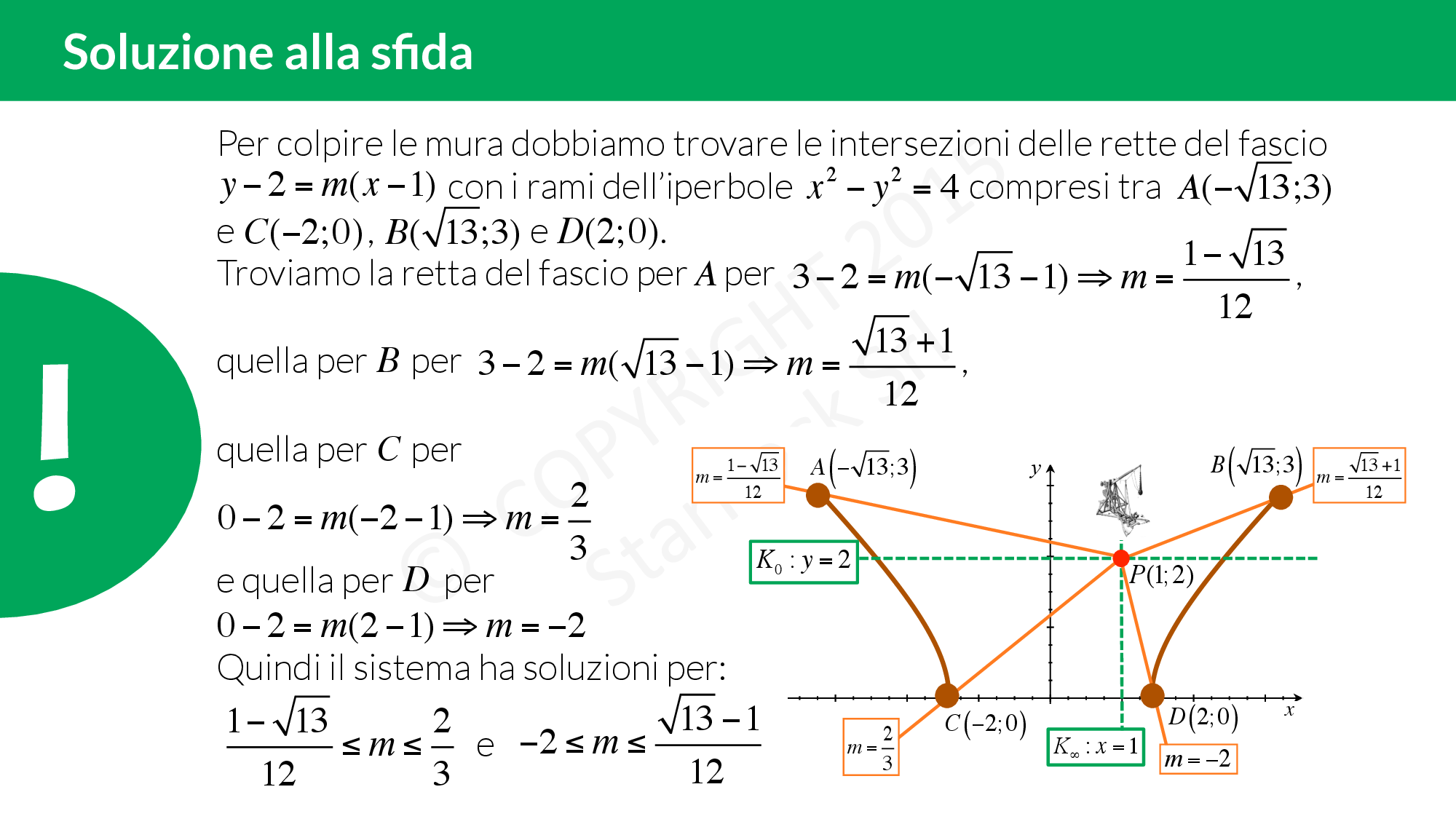
Soluzione:
Sistemi parametrici con l'iperbole - Galleria
Le mura dei castelli sono descritte da un sistema matematico! Devi trovare il modo di colpire entrambe le cinte murarie con la catapulta, come fai? Prova a risolvere la sfida e poi corri ad allenarti con gli esercizi sui sistemi parametrici con l’iperbole!