Sistemi parametrici con l'ellisse: risoluzione

Uno dei campi più studiati della matematica è quello della geometria analitica, che permette di esplorare e comprendere le forme geometriche attraverso equazioni e sistemi coordinati.

Uno degli argomenti più interessanti in questo ambito è l’analisi delle curve definite parametricamente, tra cui spicca l’ellisse, definita come il luogo geometrico dei punti per i quali la somma delle distanze da due punti fissi, detti fuochi, è costante.

Questa definizione, pur essendo geometricamente intuitiva, diventa più complessa e dettagliata quando l’ellisse è espressa attraverso un sistema di equazioni parametriche. Tali sistemi permettono di descrivere l’ellisse in termini di un parametro, tipicamente denotato con $t$, che varia su un intervallo di valori reali, fornendo una rappresentazione continua e fluida della curva.

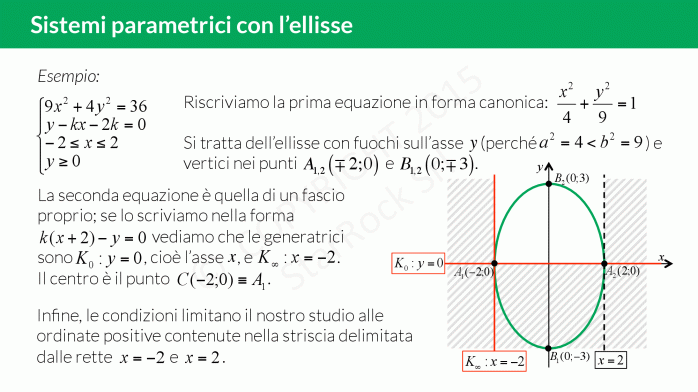
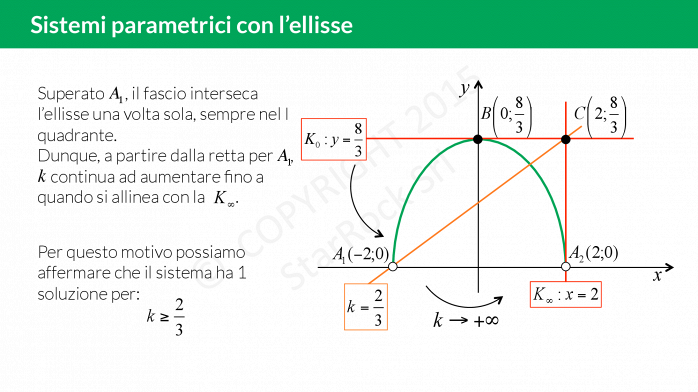
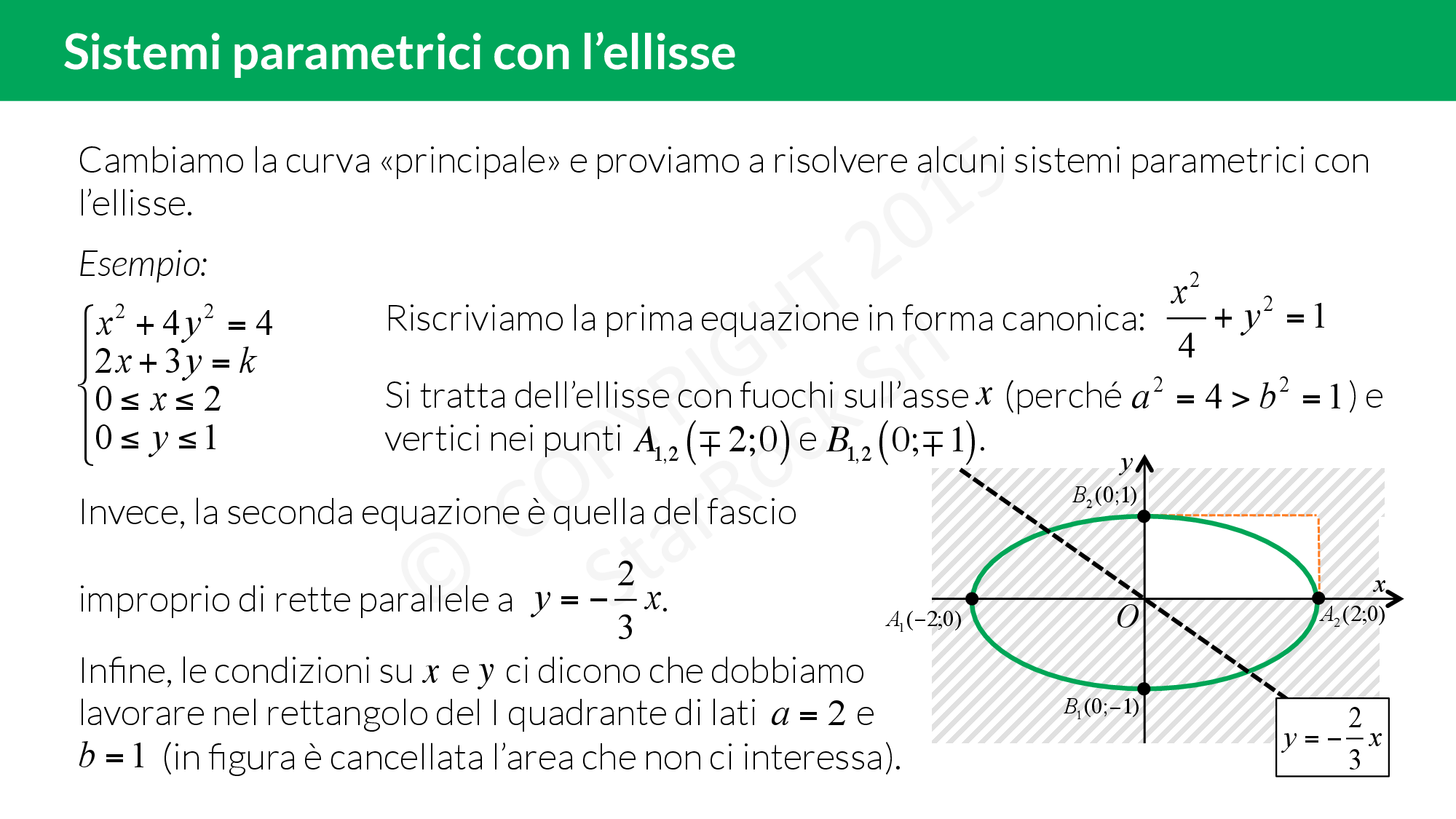
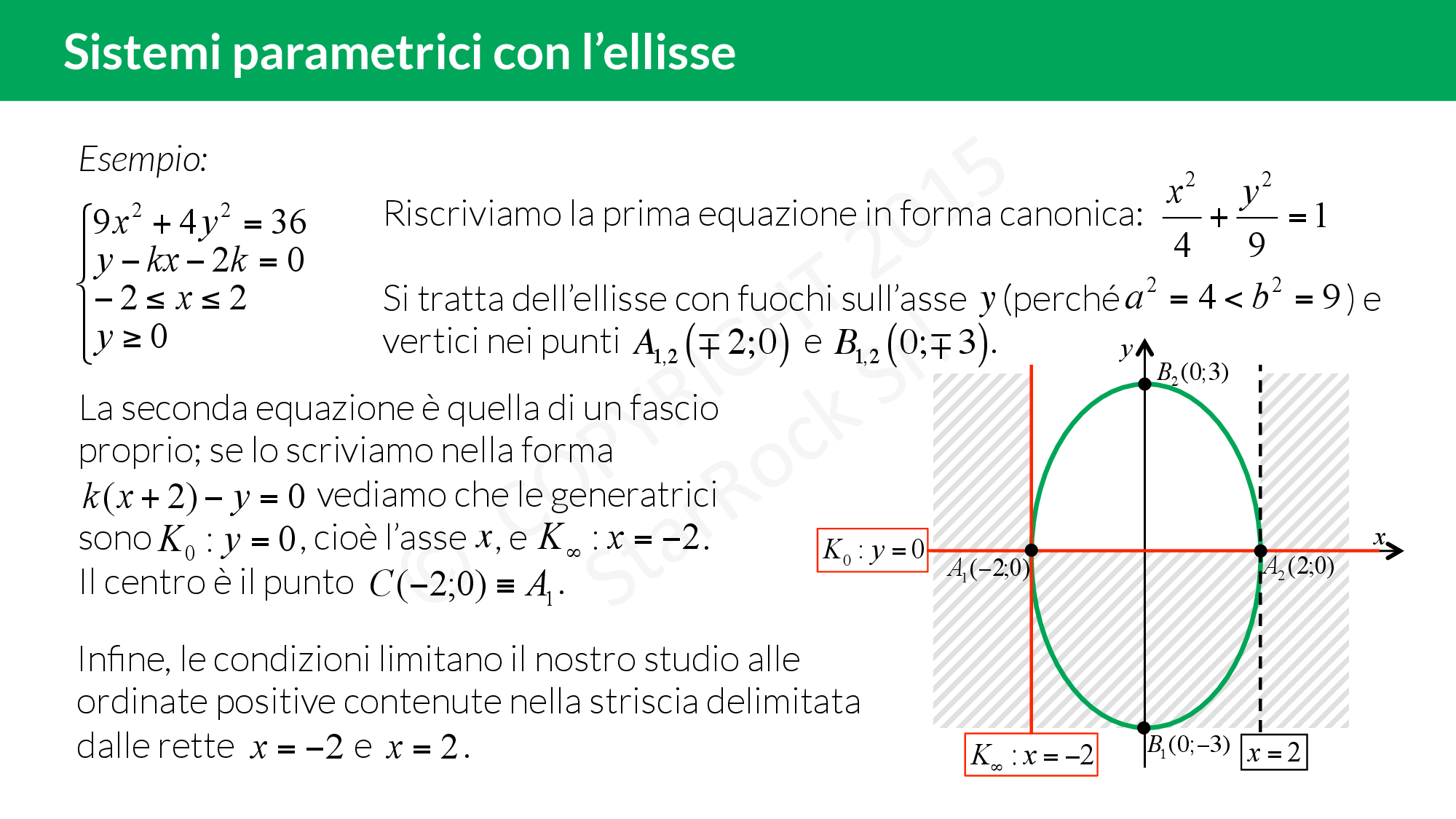
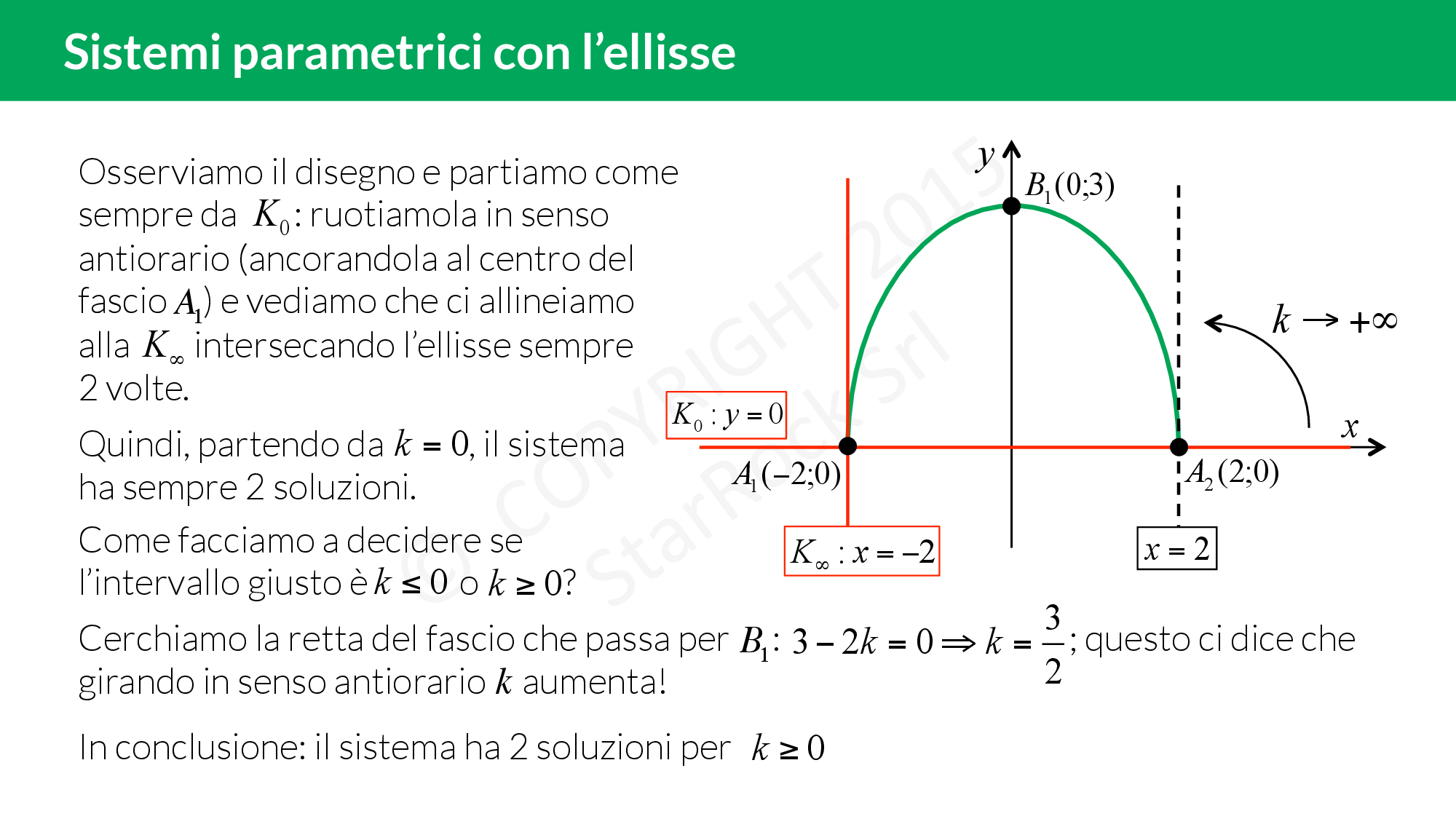
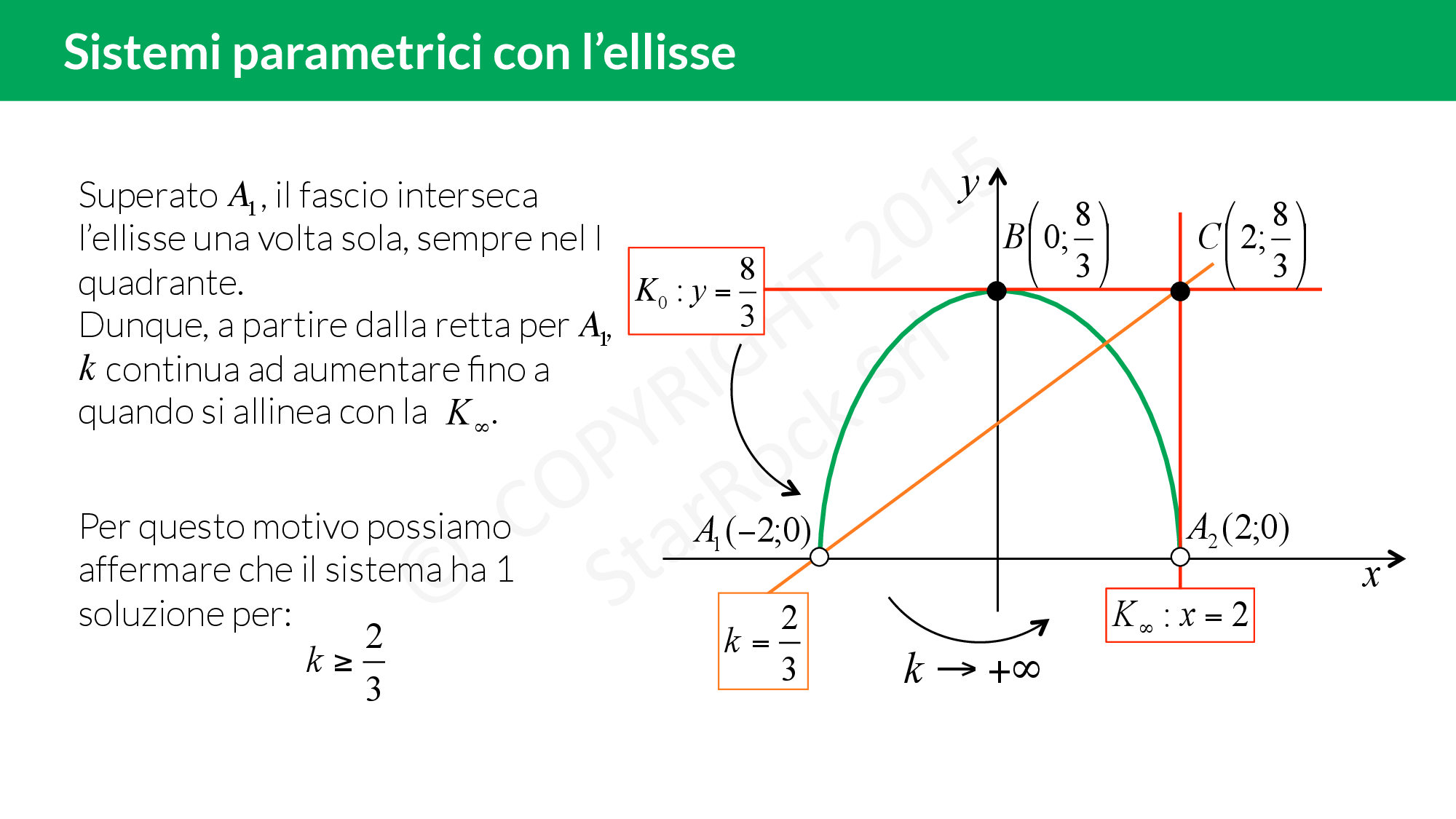
Impariamo a risolvere i sistemi parametrici in cui compare l’equazione di un’ellisse:

• per prima cosa imponi le limitazioni (se ce ne sono nel sistema) su £$x$£ e £$y$£ così da “cancellare” delle parti di piano;
• traccia il grafico delle funzioni senza il parametro;
• infine fai variare il parametro della funzione mancante per scoprire le intersezioni con le altre curve.

• Cosa sono i sistemi parametrici
• Sistemi parametrici con l'ellisse
• Interrogazione su sistemi parametrici con l'ellisse
• Sfida sui sistemi parametrici con l'ellisse

Cosa sono i sistemi parametrici

I sistemi parametrici rappresentano un concetto fondamentale nella matematica, utilizzati per descrivere insiemi di equazioni che esprimono le coordinate dei punti di una curva o superficie in funzione di uno o più parametri. Questa rappresentazione è particolarmente potente perché permette di manipolare e analizzare le forme geometriche con grande flessibilità e precisione.

In un sistema parametrico, le coordinate di un punto nello spazio, come x, y (e z per spazi tridimensionali), sono definite come funzioni di uno o più parametri indipendenti. Ad esempio, un sistema parametrico in due dimensioni potrebbe essere definito come segue:

• x=f(t)
• y=g(t)

dove t è il parametro, mentre f e g sono funzioni che descrivono come le coordinate x e y cambiano al variare di t.

Sistemi parametrici con l’ellisse

Sistemi parametrici con l'ellisse - Galleria

Qui trovi tre esercizi svolti sulla risoluzione dei sistemi parametrici in cui la conica principale è un’ellisse.

Lo svolgimento non è tanto diverso da quanto facevi quando avevi un sistema parametrico con la circonferenza o con la parabola!

Interrogazione su sistemi parametrici con l’ellisse

Cosa ti chiederà la prof domani nell’interrogazione sui sistemi parametrici con l’ellisse? Prova a risolvere i sistemi che trovi qui: sarà un’ottimo allenamento! Poi corri a fare gli esercizi!

Sfida sui sistemi parametrici con l’ellisse

Sfida:

Sistemi parametrici con l'ellisse - Galleria

Soluzione:

Sistemi parametrici con l'ellisse - Galleria

Ancora una sfida! Il castello ha le mura a forma di arco di ellisse descritta da un certo sistema matematico. Quali indicazioni devi dare per colpire almeno una volta con la catapulta i bastioni? Prova a dare una risposta: se non ti viene in mente nulla leggi la spiegazione nella soluzione!