Fasci di rette: propri e impropri
I fasci di rette propri e impropri sono concetti fondamentali nella geometria analitica, utilizzati per descrivere collezioni di rette che hanno caratteristiche specifiche in comune.
Un fascio proprio di rette è un insieme di rette che passano tutte per un punto comune, detto punto base del fascio. Questo punto funge da vertice da cui tutte le rette del fascio “emanano", simile ai raggi di una stella. Il fascio proprio è quindi definito dalla presenza di questo punto di intersezione unico.
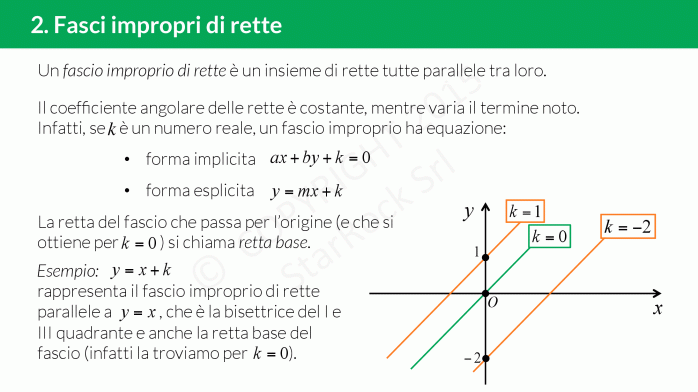
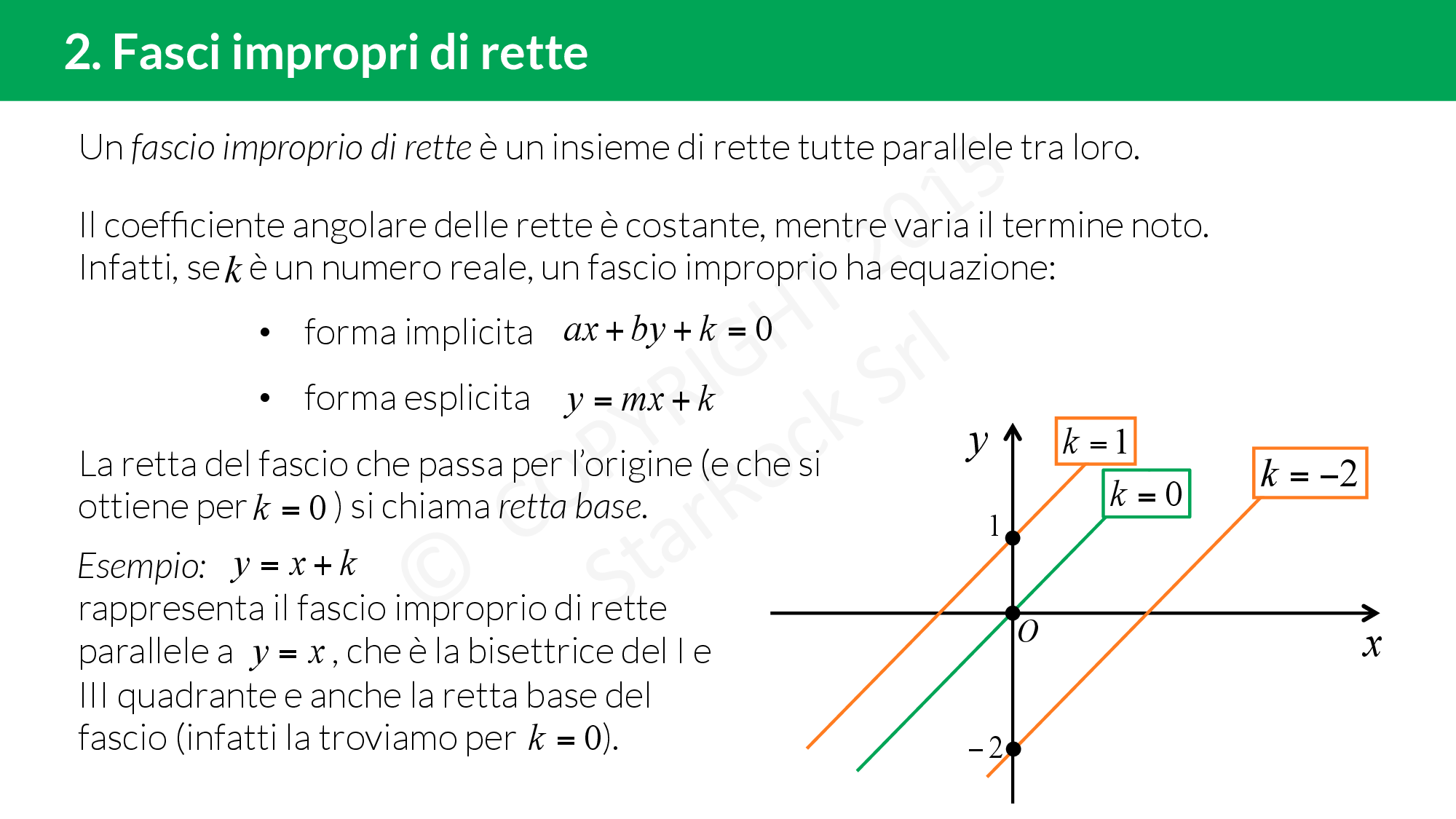
Al contrario, un fascio improprio di rette consiste in rette che sono parallele tra loro. In questo caso, non esiste un punto di intersezione finito; piuttosto, si può dire che le rette si incontrano all’infinito. I fasci impropri sono spesso descritti nel contesto della geometria proiettiva, dove i punti all’infinito giocano un ruolo cruciale.
Cominciamo da un bel ripasso di fasci di rette propri e impropri, poi vediamo come si studia un fascio e quali sono le sue applicazioni.
Prima di iniziare lo studio dei sistemi parametrici, è bene ripassare i fasci di rette. Ricordi cosa sono?
I fasci di rette sono insiemi di rette con una caratteristica in comune. Ci sono due tipi:
- fasci di rette propri: tutte le rette sono incidenti in uno stesso punto detto centro del fascio;
- fasci di rette impropri: tutte le rette sono parallele.
- Fasci di rette
- Come studiare un fascio di rette
- Esercizi sui fasci di rette
- Sfida sui fasci di rette
Fasci di rette
Fasci di rette propri
Fasci di rette impropri
Cos’è un fascio di rette? È un insieme di rette che hanno una proprietà in comune. Abbiamo due tipi di fascio di rette:
- fascio di rette proprio: è l’insieme delle rette che passano tutte per un stesso punto, detto centro del fascio;
- fascio di rette improprio: è l’insieme delle rette parallele a una retta data. Essendo parallele, hanno tutte lo stesso coefficiente angolare.
Per capire se un fascio di rette sia proprio o improprio, basta guardare il coefficiente angolare delle rette del fascio: se dipende dal parametro (variabile) allora è un fascio di rette proprio, altrimenti è improprio.
Ad esempio, l’insieme delle rette £$y=kx+4$£ è un fascio di rette proprio, perché al variare di £$k$£ cambia anche il coefficiente angolare. Il fascio di rette £$y=3x+2k$£ è invece un fascio di rette improprio perché il coefficiente angolare delle rette è costante (uguale a £$3$£) e cambia solo il termine noto.
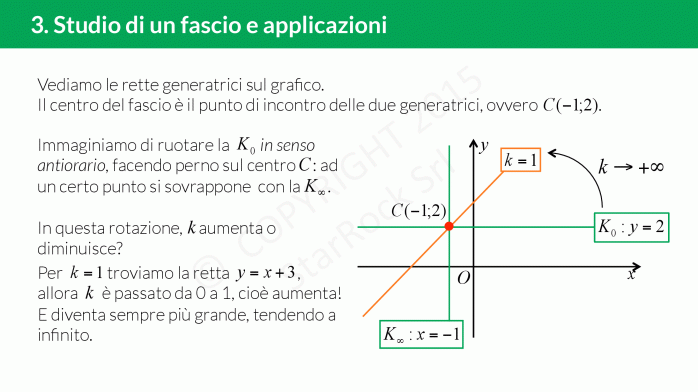
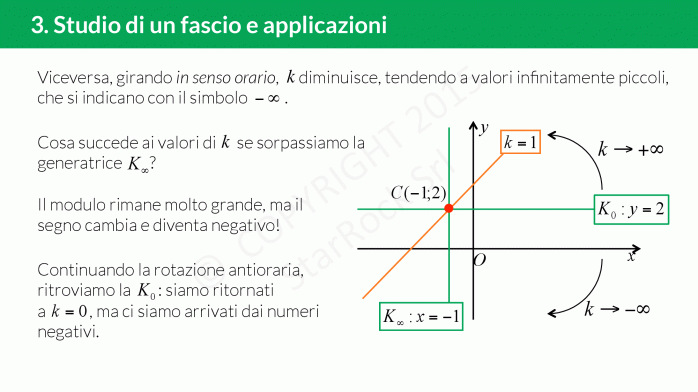
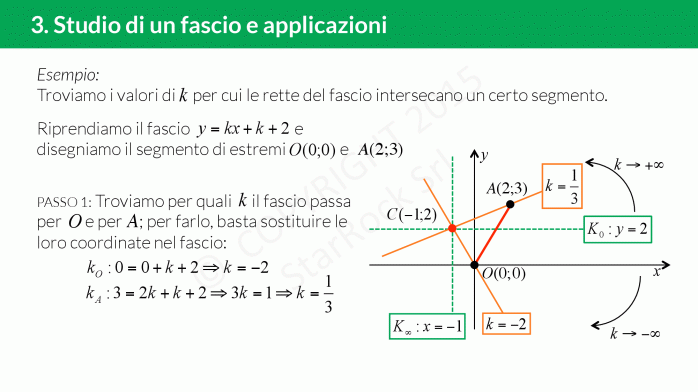
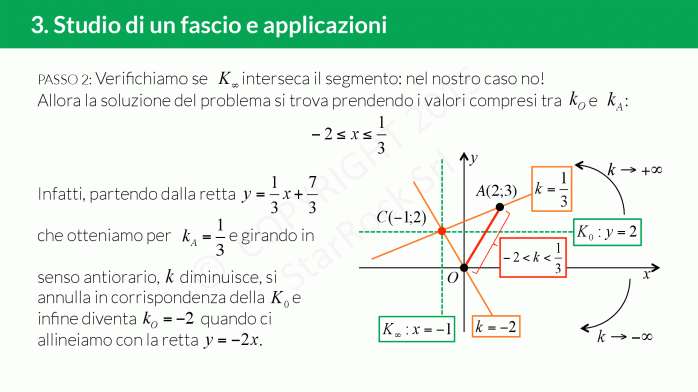
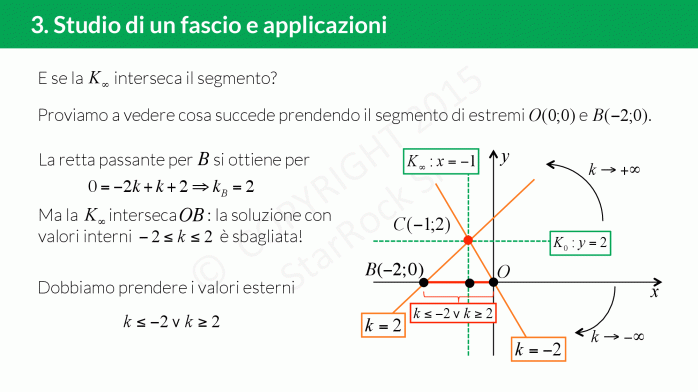
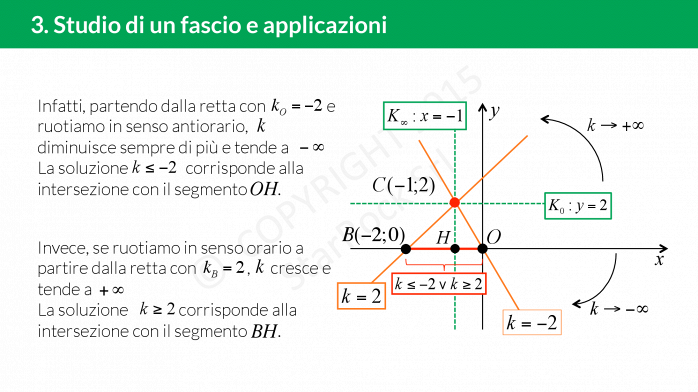
Come studiare un fascio di rette
Per studiare un fascio di rette dobbiamo capire se è proprio oppure improprio: basta guardare se il coefficiente angolare dipende dal parametro (di solito indicato con £$k$£);
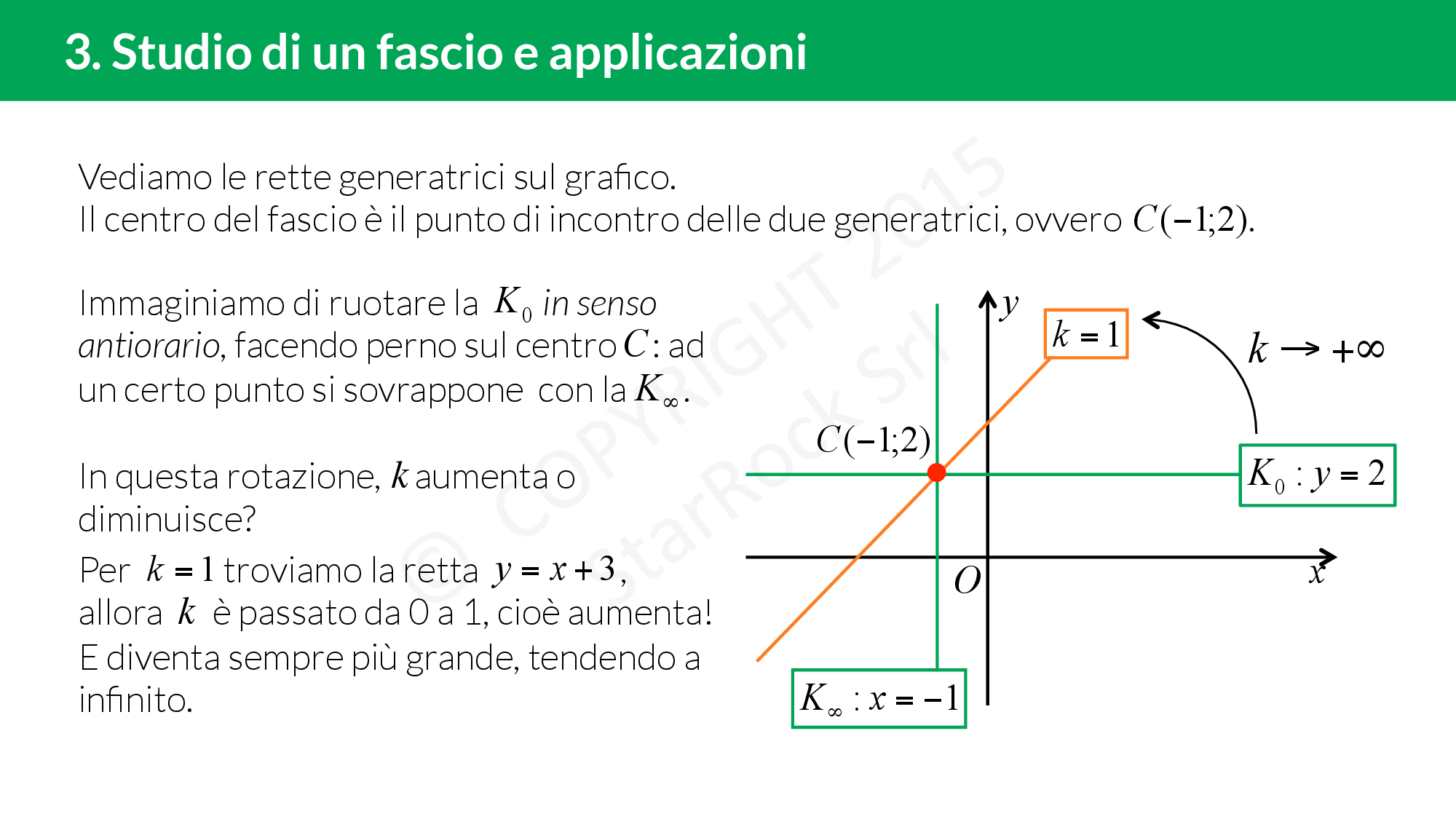
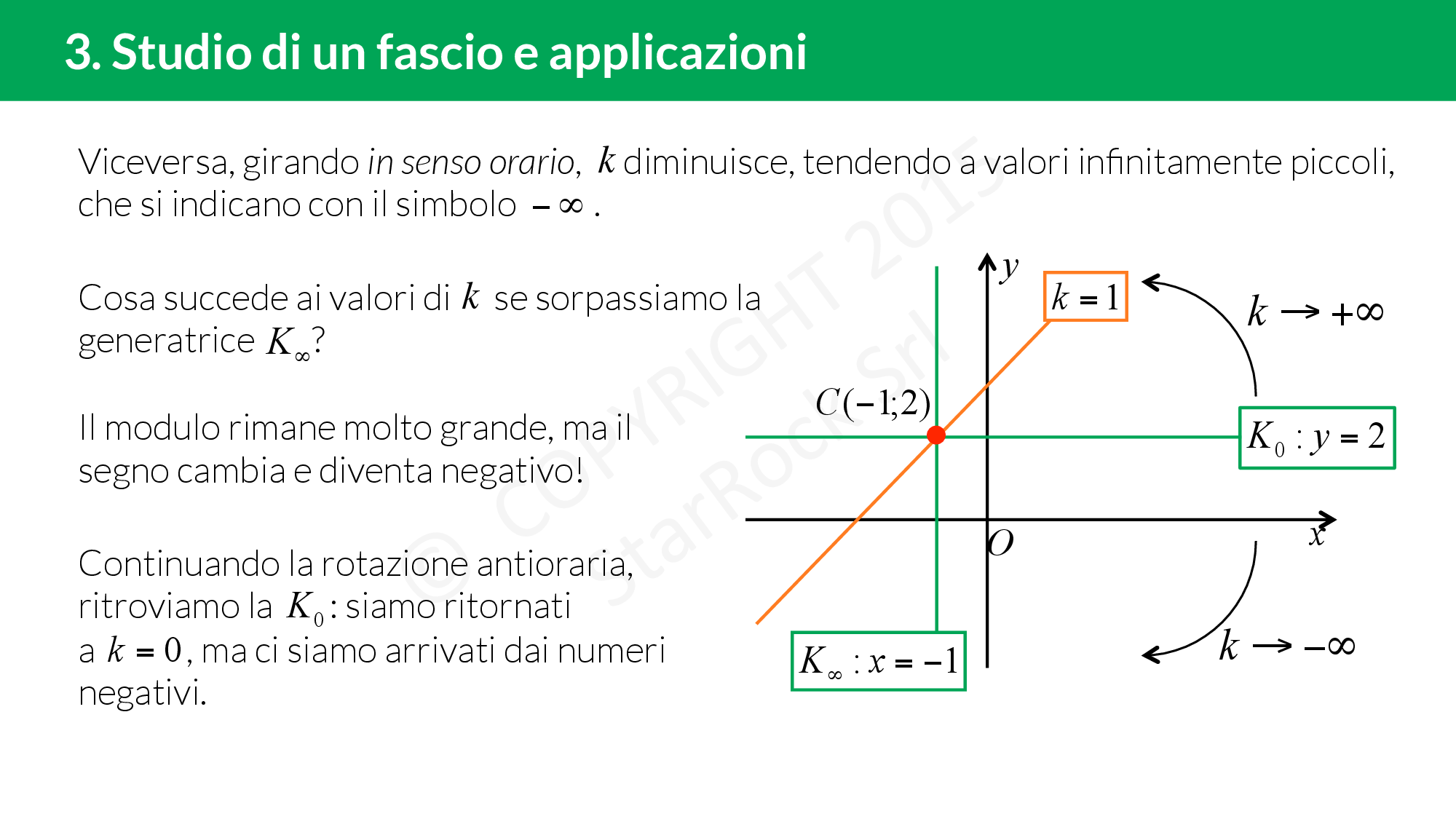
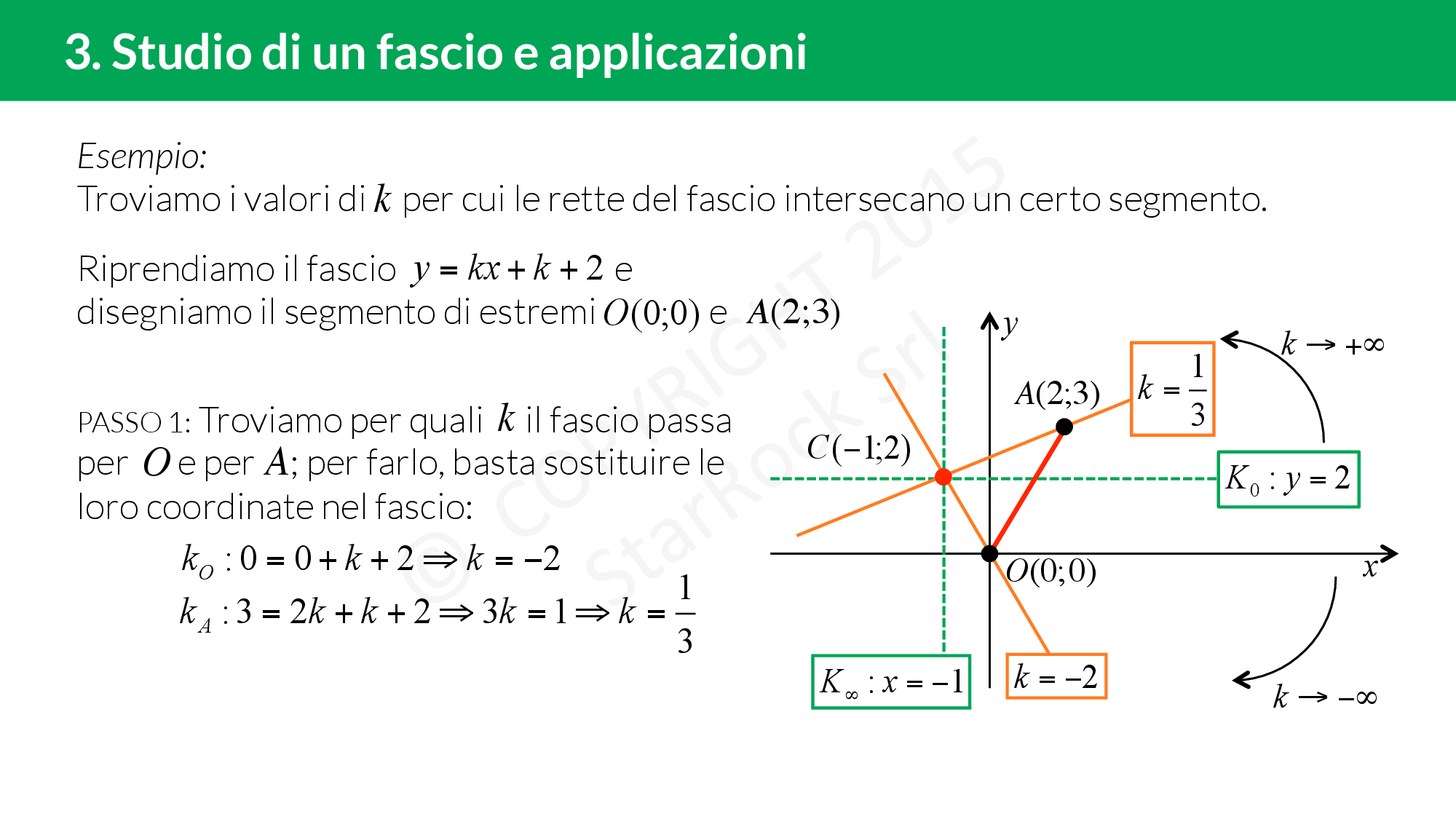
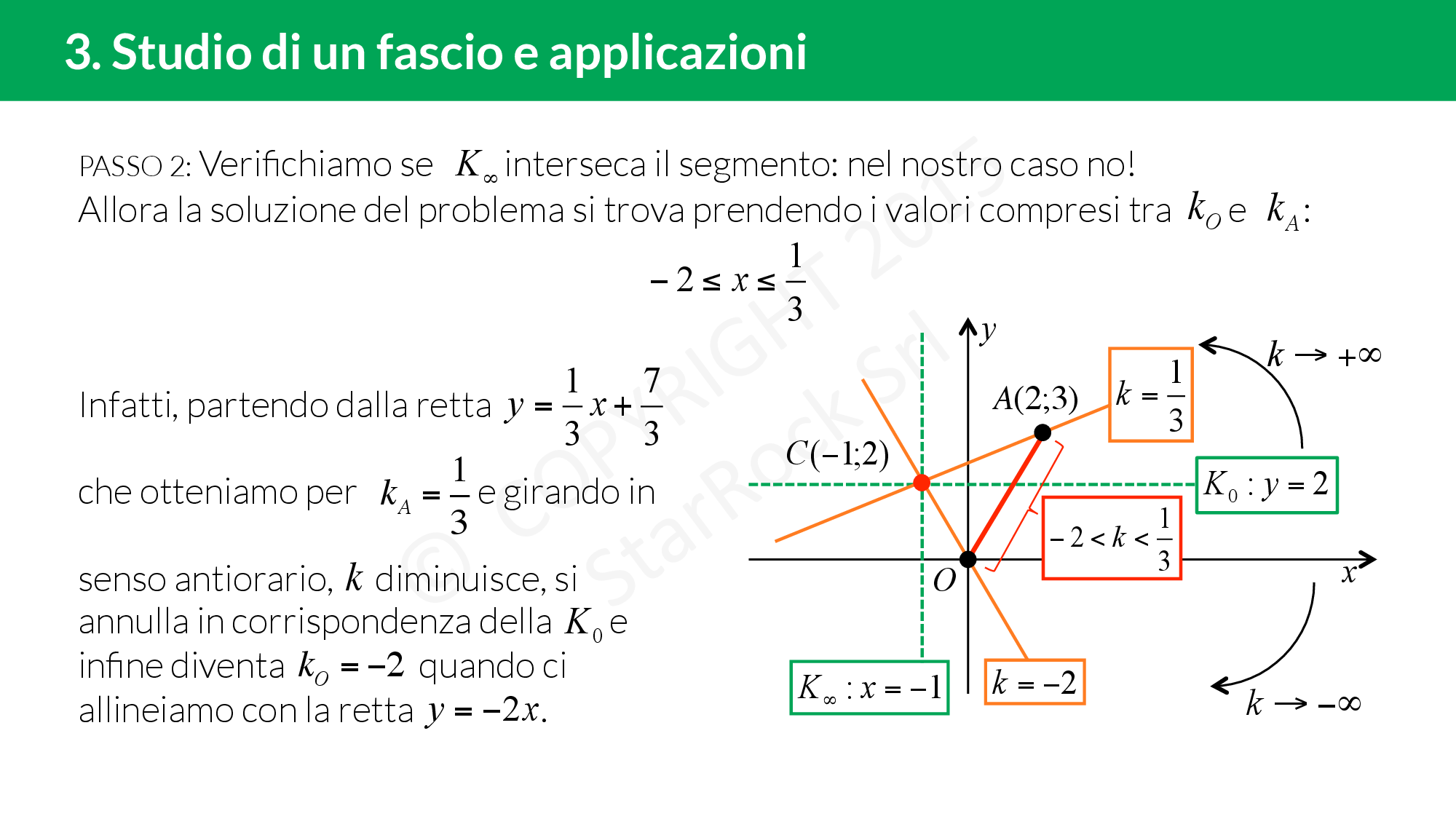
- se è proprio, troviamo le due generatrici e il centro del fascio;
- se è improprio, è sufficiente studiare la retta con £$k=0$£ e poi studiare al variare del parametro come sono fatte le rette.
Ovviamente lo studio del fascio di rette non finisce qui. Guarda la lezione per scoprire tutti i passaggi!
Esercizi sui fasci di rette

Ora che hai fatto un ripasso dei fasci di rette, mettiti alla prova con questi esercizi!
Sfida sui fasci di rette
Testo della sfida
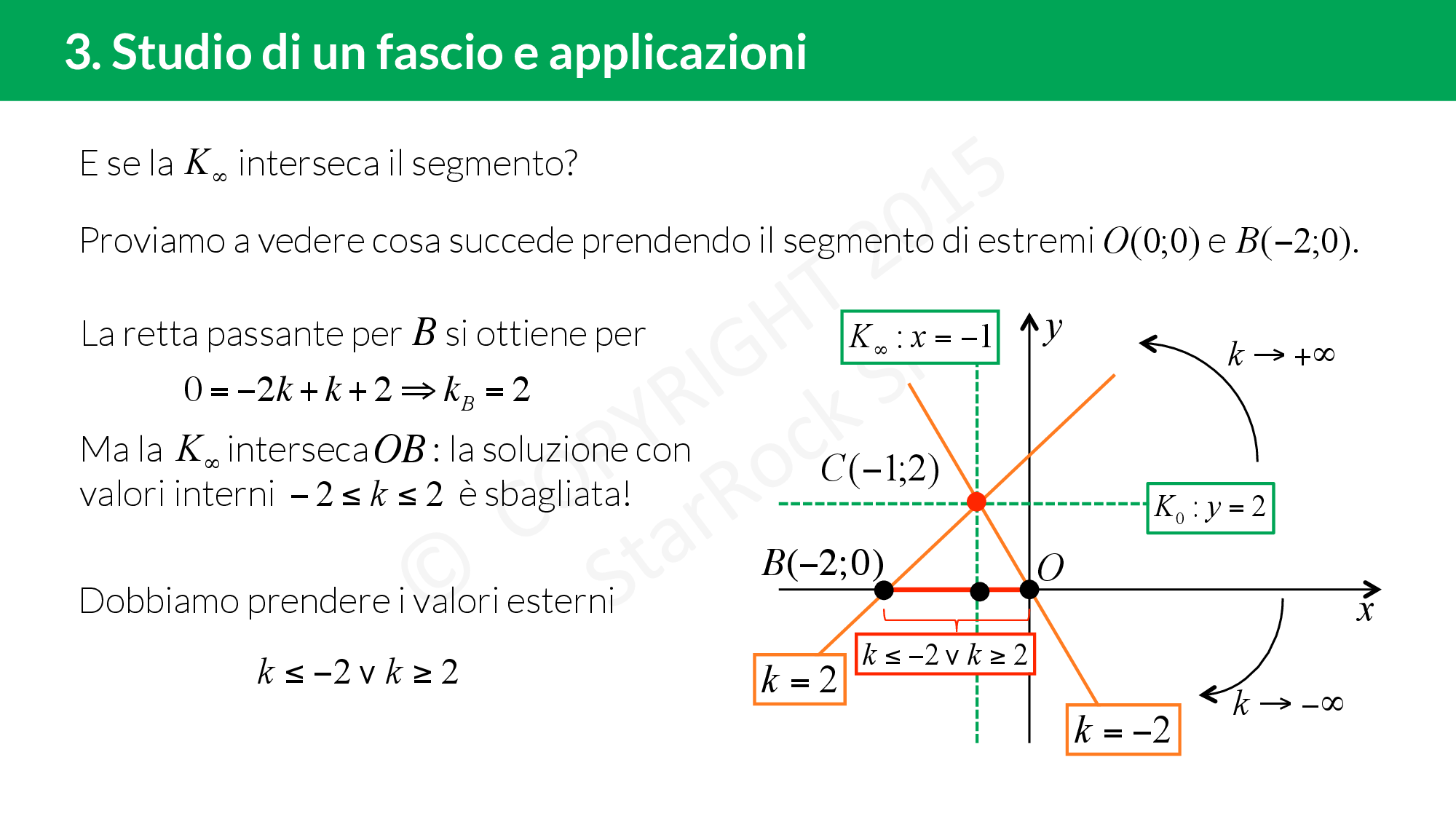
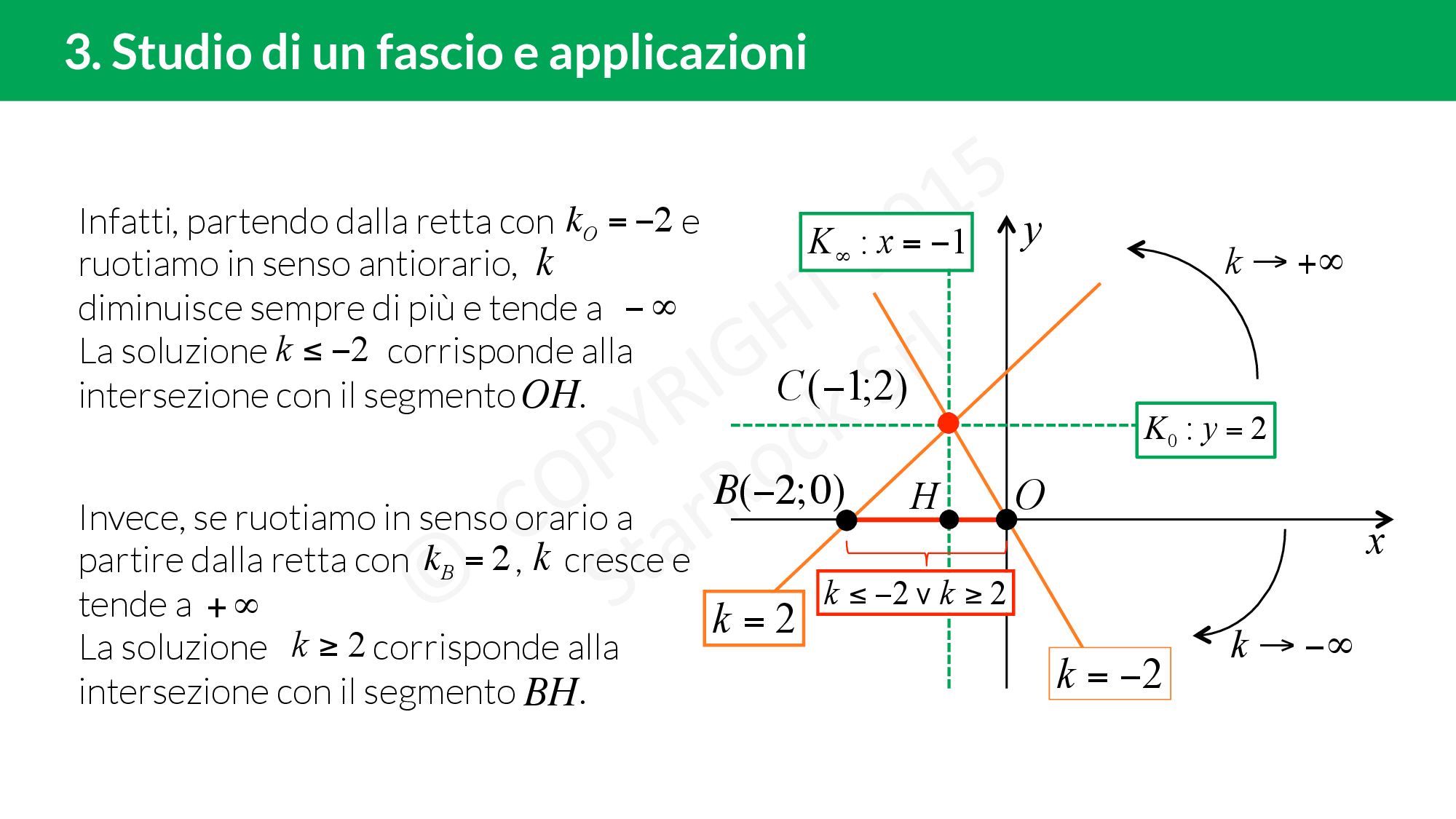
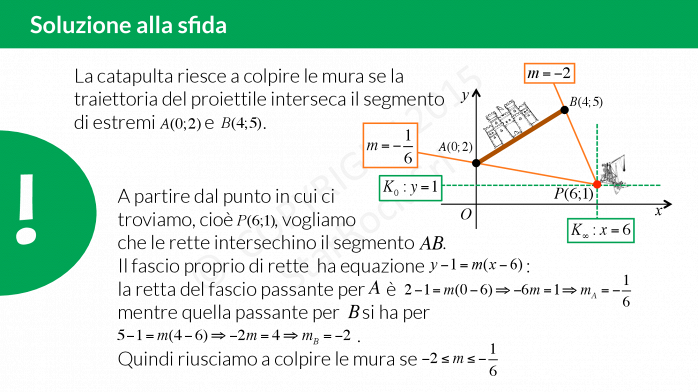
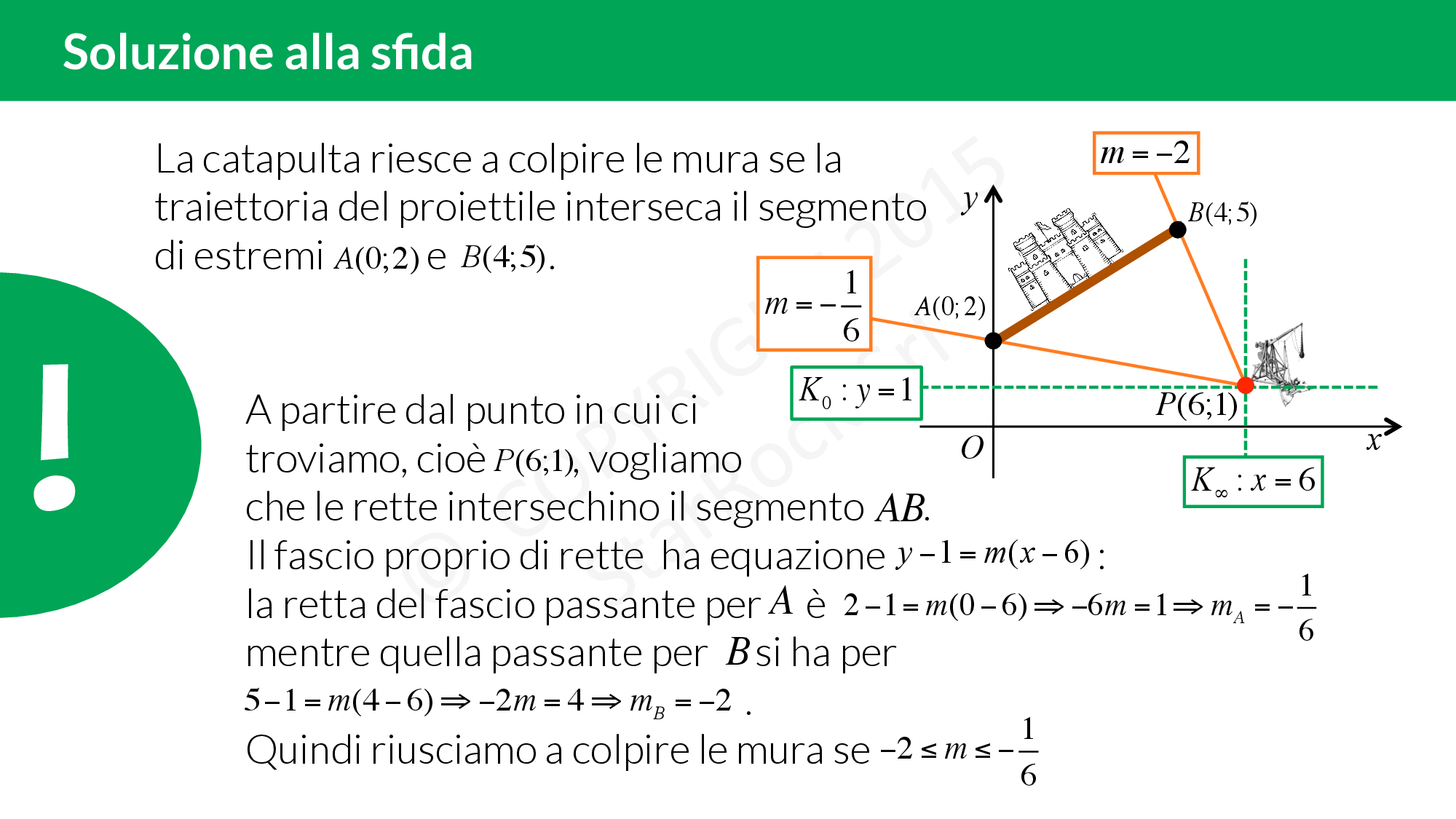
Soluzione alla sfida
Per vincere la sfida del tuo gioco del PC devi conoscere come usare i fasci di rette! Sei pronto?