Le funzioni goniometriche inverse: definizione
Le funzioni goniometriche inverse sono un insieme di funzioni utilizzate per calcolare gli angoli associati ai valori delle funzioni goniometriche. Sono utili quando si vuole determinare l’angolo che corrisponde a un determinato valore di una funzione goniometrica.
Ad esempio, se si conosce il seno di un angolo, l’arcoseno può essere usato per trovare l’angolo stesso. Arcoseno, arcocoseno, arcotangente e arcocotangente sono le funzioni inverse di seno, coseno, tangente e cotangente. Impara a conoscerle e a calcolare l’angolo x sapendo quanto vale senx, cosx, tgx e cotgx.
Scopriamo quali sono i sottoinsiemi del dominio delle funzioni goniometriche in cui sono invertibili e troviamo le caratteristiche delle funzioni inverse.
In questa lezione vedremo:
- Funzione arcoseno: definizione, dominio e codominio dell’arcoseno
- Funzione arcocoseno: definizione, dominio e codominio dell’arcocoseno
- Funzione arcotangente: definizione, dominio e codominio dell’arcotangente
- Funzione arcocotangente: definizione, dominio e codominio dell’arcocotangente.
Una funzione è invertibile se e solo se è biunivoca.
- Tabella delle caratteristiche delle funzioni seno, coseno, tangente e cotangente
- Funzione arcoseno
- Funzione arcocoseno
- Funzione arcotangente
- Funzione arcocotangente
- Ripassa per l'interrogazione sulle funzioni goniometriche inverse
Tabella delle caratteristiche delle funzioni seno, coseno, tangente e cotangente
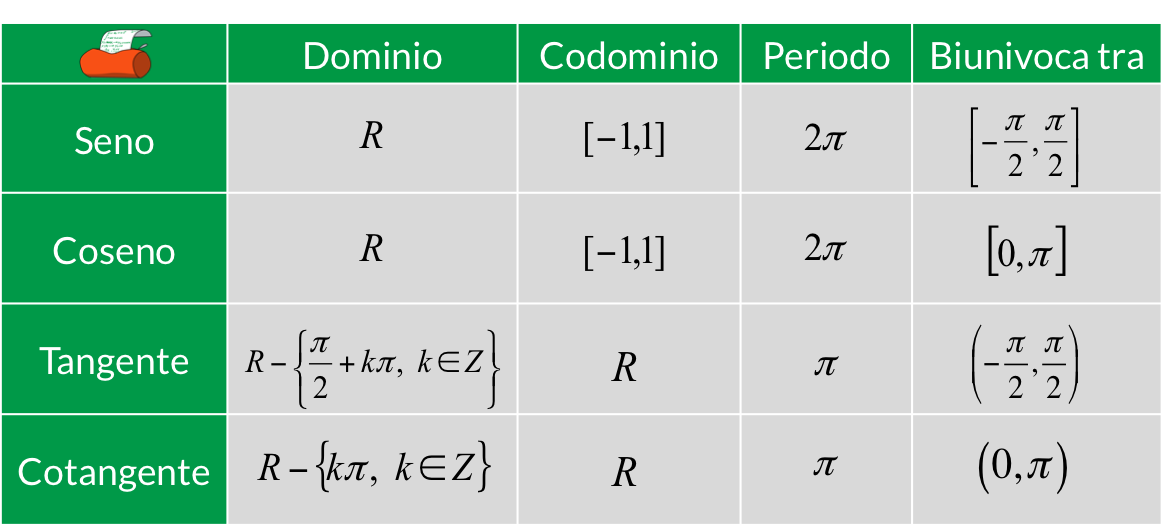
Tabella tutte le caratteristiche delle funzioni seno, coseno, tangente e cotangente.
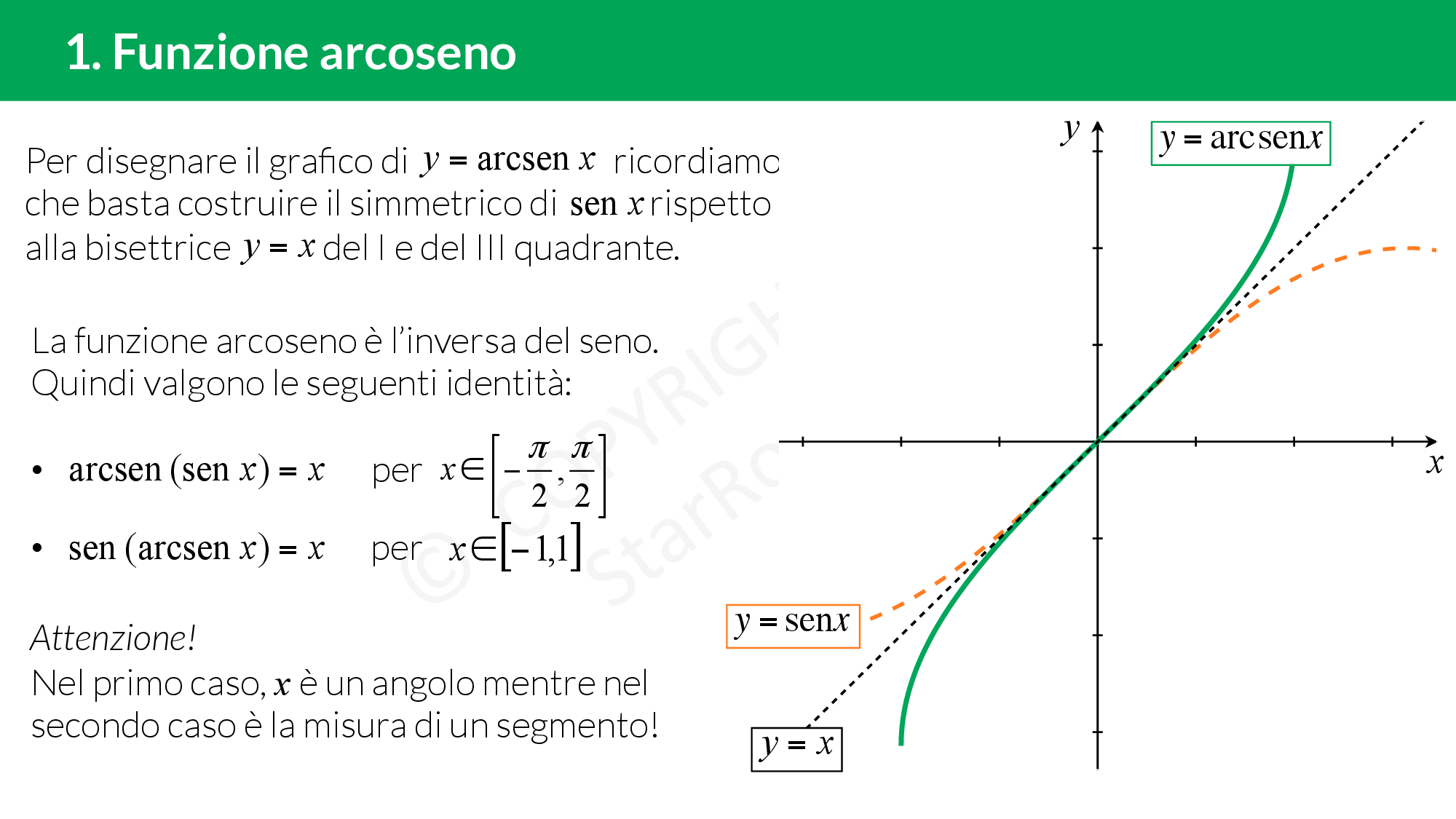
Funzione arcoseno
£$f(x)=sen \ x $£ è una funzione biunivoca nell’intervallo £$\left[-\frac{\pi}{2},\frac{\pi}{2} \right]$£, quindi è invertibile se restringiamo il suo dominio all’intervallo £$\left[-\frac{\pi}{2},\frac{\pi}{2} \right]$£. La funzione inversa si chiama arcoseno ed è indicata con £$g(x)=f^{-1}(x)=arcsen \ x$£.
Il dominio dell’arcoseno è £$[-1,1]$£, che era il codominio della funzione seno.
Il codominio dell’arcoseno è £$\left[-\frac{\pi}{2},\frac{\pi}{2} \right]$£ che è il sottoinsieme del dominio del seno in cui la funzione è invertibile.
Funzione arcocoseno
£$f(x)=cos \ x$£ è una funzione invertibile nel sottoinsieme del dominio in cui è biunivoca, cioè £$\left[0,\pi \right]$£. La funzione inversa si chiama arcocoseno ed è indicata con £$g(x)=f^{-1}(x)=arccos\ x$£.
Il dominio dell’arcocoseno è £$[-1,1]$£, che era il codominio della funzione coseno.
Il codominio dell’arcoseno è £$\left[0,\pi \right]$£ che è il sottoinsieme del dominio del coseno in cui la funzione è invertibile.
Funzione arcotangente
£$f(x)=tg \ x$£ è una funzione invertibile nel sottoinsieme del dominio in cui è biunivoca, cioè £$\left(-\frac{\pi}{2},\frac{\pi}{2} \right)$£.
La funzione inversa si chiama arcotangente ed è indicata con £$g(x)=f^{-1}(x)=arctg\ x$£.
Il dominio dell’arcotangente è £$\mathbb{R}$£, che era il codominio della funzione tangente.
Il codominio dell’arcotangente è £$\left(-\frac{\pi}{2},\frac{\pi}{2} \right)$£ che è il sottoinsieme del dominio della tangente in cui la funzione è invertibile.
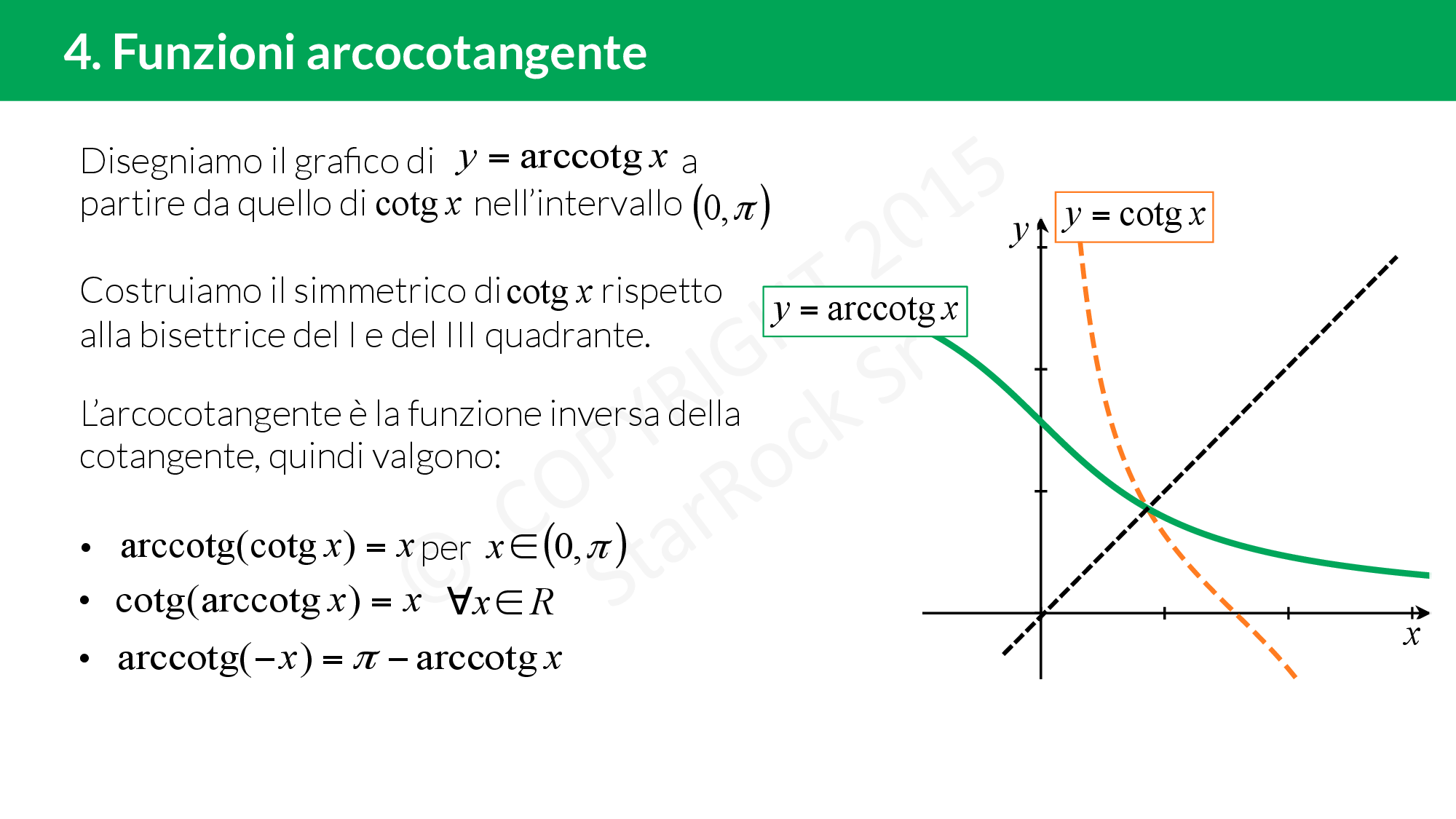
Funzione arcocotangente
£$f(x)=cotg \ x$£ è una funzione invertibile nel sottoinsieme del dominio in cui è biunivoca, cioè £$\left(0,\pi \right)$£.
La funzione inversa si chiama arcotangente ed è indicata con £$g(x)=f^{-1}(x)=arccotg\ x$£.
Il dominio dell’arcotangente è R, che era il codominio della funzione cotangente.
Il codominio dell’arcocotangente è £$\left(0,\pi \right)$£ che è il sottoinsieme del dominio della cotangente in cui la funzione è invertibile.
Ripassa per l’interrogazione sulle funzioni goniometriche inverse
Ora che hai visto quali sono le funzioni goniometriche inverse, prova a risolvere questi esercizi per vedere se sei pronto per l’interrogazione!