Circonferenza goniometrica, seno e coseno in geometria
Nel mondo della geometria, la circonferenza goniometrica insieme alle funzioni seno e coseno giocano un ruolo cruciale nella comprensione delle relazioni tra gli angoli e le lunghezze nei triangoli e oltre.
Partiremo dalla circonferenza goniometrica, uno strumento essenziale che rappresenta tutti gli angoli possibili in un sistema di coordinate cartesiane, dove ogni punto sulla circonferenza è definito dalle coordinate (cos(θ), sin(θ)).
In questa lezione troverai tutto quello che ti serve per imparare ad usare la circonferenza goniometrica, seno e coseno! Imparerai:
- Circonferenza goniometrica: cosa è la circonferenza goniometrica, come si individua un angolo sulla circonferenza goniometrica
- Seno, coseno e prima relazione fondamentale: seno e coseno come coordinate di un punto sulla circonferenza goniometrica, limitazioni di seno e coseno, definizione e spiegazione della prima relazione fondamentale della goniometria
- Seno e coseno degli angoli principali: tabella con i valori principali di seno e coseno per angoli compresi fra £$ e [iol_placeholder type="formula" engine="katex" display="inline"]2 \pi$£
- Periodicità di seno e coseno: quale è la periodicità di seno e coseno, cioè quando i valori di seno e coseno si ripetono sempre uguali.
- Tabella con i valori di seno e coseno degli angoli principali
- La circonferenza goniometrica
- Seno, coseno e prima relazione fondamentale
- Seno e coseno degli angoli principali
- Periodicità di seno e coseno
- Ripassa per l'interrogazione su seno e coseno in geometria
- Sfida su seno e coseno
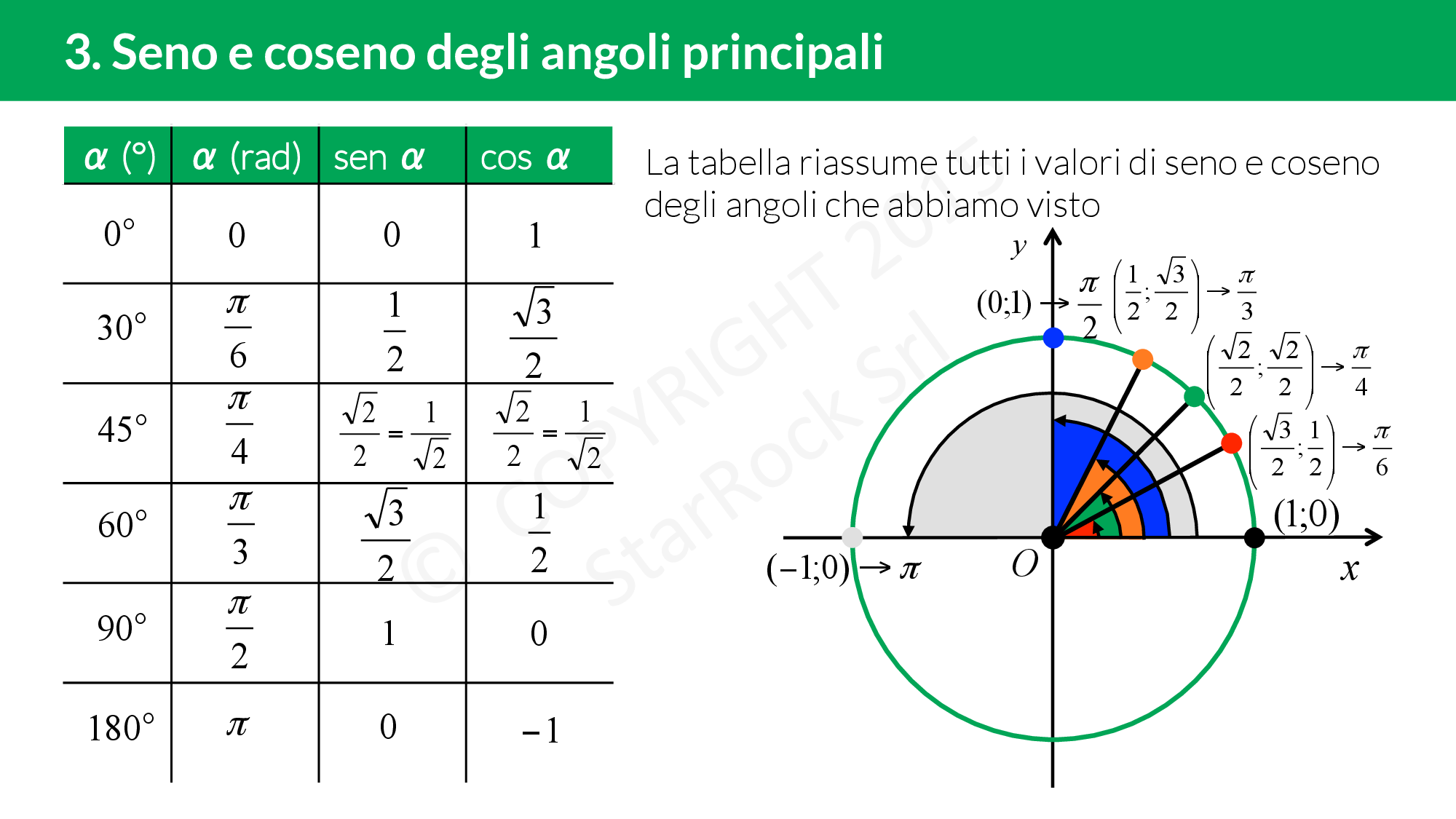
Tabella con i valori di seno e coseno degli angoli principali
Seno e coseno degli angoli principali: tabella con i valori principali di seno e coseno per angoli compresi fra £$ e [iol_placeholder type="formula" engine="katex" display="inline"]\pi$£
La circonferenza goniometrica
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
La circonferenza goniometrica è una circonferenza centrata nell’origine e di raggio 1. La sua equazione è £$x^2+y^2=1$£
Rappresentiamo sulla circonferenza goniometrica tutti gli angoli orientati ed i corrispondenti archi di circonferenza. Il primo lato di ogni angolo giace sulla parte positiva dell’asse £$x$£, quindi “l’origine degli archi" è il punto di coordinate £$A(1;0)$£. Tutti gli altri archi saranno:
- positivi se il secondo lato dell’angolo si muove in senso antiorario;
- negativi se il secondo lato dell’angolo si muove in senso orario.
Seno, coseno e prima relazione fondamentale
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
Ogni angolo sulla circonferenza goniometrica è individuato da un lato orizzontale, sull’asse £$x$£, che incontra la circonferenza in £$A(1;0)$£ e dal secondo lato che incontra la circonferenza in un unico punto £$P(x_P;y_P)$£. Ad ogni angolo £$\alpha$£, quindi, possiamo associare univocamente un punto £$P$£ in cui:
£$\begin{cases}x_P=cos \ \alpha \\ y_P=sen \ \alpha \end{cases}$£.
Da questa associazione possiamo dire che:
- £$\begin{cases}-1 \le x_P \le 1 \Rightarrow -1 \le cos \ \alpha \le 1 \\ -1 \le y_P \le 1 \Rightarrow -1 \le sen \ \alpha \le 1 \end{cases}$£
perché la circonferenza goniometrica ha raggio 1; - £$cos^2 \ \alpha + sen^2 \ \alpha=1$£ perché £$P(x_P=cos \ \alpha; y_P=sen \ \alpha)$£ appartiene alla circonferenza di equazione £$x^2+y^2=1$£ questa è la prima relazione fondamentale della goniometria!
Seno e coseno degli angoli principali
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
Non sempre è facile calcolare il seno e il coseno degli angoli. Fortunatamente però per alcuni angoli, conosciamo i loro valori. Questi devi assolutamente impararli perché te li ritroverai di fronte un sacco di volte.
Nella lezione, vedrai la dimostrazione dei valori di seno e coseno degli angoli fondamentali. In più c’è anche una tabella riassuntiva: cosa vuoi di più?
Periodicità di seno e coseno
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
Il seno ed il coseno sono periodici di £$2\pi$£. Questo significa che, dopo aver fatto un giro completo della circonferenza, ossia aggiungendo o togliendo multipli di £$2\pi$£, i valori di seno e coseno si ripetono uguali:
- £$sen(\alpha+2k\pi)=sen \ \alpha$£ con £$k \in \mathbb{Z}$£;
- £$cos(\alpha+2k\pi)=cos \ \alpha$£ con £$k \in \mathbb{Z}$£.
Ripassa per l’interrogazione su seno e coseno in geometria
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
Verifica se ti ricordi i valori di seno e coseno degli angoli principali. Sì ma quali sono? Se hai dubbi, riguarda la lezione oppure allenati con gli esercizi su seno e coseno!
Sfida su seno e coseno
Testo:
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
Soluzione:
Circonferenza goniometrica, seno e coseno: punto di vista geometrico - Galleria
Sei su una giostra che all’improvviso si blocca! Cosa farai? Ma soprattutto, a che altezza sei da terra? Grazie alla goniometria, potrai dare la risposta!
Eh, ma rimani comunque bloccato. Speriamo arrivi qualcuno a salvarti!