Funzioni seno e coseno: grafici e definizione
Il seno e il coseno, pilastri fondamentali della trigonometria, sono funzioni che descrivono le relazioni tra gli angoli e i lati di un triangolo rettangolo.
Al centro di queste funzioni c’è la loro dipendenza da un angolo, che permette di esplorare la loro natura periodica e le loro applicazioni ben al di là dei confini della geometria classica. Attraverso l’uso del cerchio unitario e l’estensione al piano cartesiano, il seno e il coseno si rivelano strumenti potenti per la rappresentazione e l’analisi di movimenti circolari e pattern ripetitivi.
Impara ad analizzare il seno e il coseno come funzioni di un angolo. Scopri quali sono le proprietà di queste funzioni e come sono i grafici di sinusoide e cosinusoide.
Vediamo dominio, codominio, simmetrie, monotonia e segno delle funzioni seno e coseno e poi disegniamo il loro grafico.
- Funzioni seno e coseno
- Proprietà delle funzioni seno e coseno
- Grafici delle funzioni seno e coseno: sinusoide e cosinusoide
- Ripassa per l'interrogazione sulle funzioni seno e coseno
- Sfida sui grafici di seno e coseno
Funzioni seno e coseno
Seno e coseno possono essere visti come l’ordinata e l’ascissa di un punto sulla circonferenza goniometrica. Questo punto è univocamente determinato dato l’angolo, ciò significa che possiamo definire seno e coseno come funzioni dell’angolo.
- Il dominio delle funzioni seno e coseno è l’insieme dei reali £$\mathbb{R}$£ perché per ogni valore £$x$£ dell’angolo possiamo trovare un punto corrispondente sulla circonferenza goniometrica.
- Il codominio delle funzioni seno e coseno è l’intervallo £$[-1,1]$£. Il punto appartiene alla circonferenza centrata nell’origine e di raggio 1, quindi avrà coordinate comprese fra £$-1$£ e £$1$£.
Proprietà delle funzioni seno e coseno
Le proprietà fondamentali delle funzioni seno e coseno sono:
- Periodicità. Seno e coseno sono periodici di £$2\pi$£, cioè assumono gli stessi valori sottraendo o sommando multipli di £$2\pi$£ all’angolo £$x$£:
- £$sen(x+2k\pi)=sen \ x$£ con £$k \in \mathbb{Z}$£;
- £$cos(x+2k\pi)=cos \ x$£ con £$k \in \mathbb{Z}$£.
La periodicità è utile perché basta studiare la funzione fra £$[0, 2\pi]$£ e poi riportarla uguale in tutti gli altri intervalli reali.
- Simmetria. Analizzando due punti simmetrici rispetto all’asse £$x$£ (o all’asse £$y$£) sulla circonferenza goniometrica si trova che:
- il coseno è una funzione pari £$cos(-x)=cos \ x $£
- il seno è una funzione dispari £$sen(-x)=-sen \ x$£.
- Segno e monotonia. Studiamo quando le funzioni seno e coseno sono positive, negative, nulle, crescenti o decrescenti.
- La funzione £$ y=sen \ x$£ è:
- positiva in £$\left( 0, \pi \right)$£
- negativa in £$\left( \pi, 2\pi\right)$£
- nulla in £$x=0, \pi$£
- crescente in £$\left[0, \frac{\pi}{2} \right] \cup \left[\frac{3}{2}\pi, 2\pi \right]$£
- decrescente in £$\left[\frac{\pi}{2}, \frac{3}{2}\pi \right]$£.
- La funzione £$ y=cos \ x$£ è:
- positiva in £$\left[ 0, \frac{\pi}{2}\right) \cup \left( \frac{3}{2}\pi, 2\pi \right]$£
- negativa in £$\left( \frac{\pi}{2}, \frac{3}{2}\pi\right)$£
- nulla in £$x=\frac{\pi}{2}, \frac{3}{2}\pi$£
- crescente in £$[\pi, 2\pi]$£
- decrescente in £$[0, \pi]$£.
- La funzione £$ y=sen \ x$£ è:
Grafici delle funzioni seno e coseno: sinusoide e cosinusoide
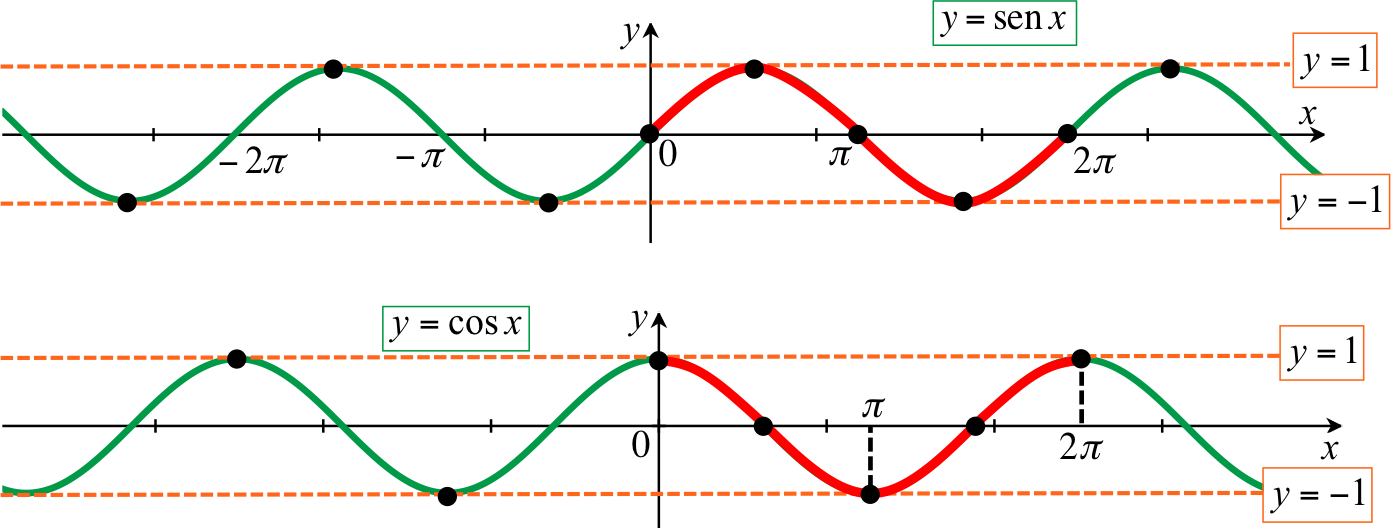
Con le informazioni viste finora sulle funzioni seno e coseno, sei in grado di disegnare il grafico di queste due funzioni:
- sinusoide: è il grafico della funzione seno;
- cosinusoide: è il grafico della funzione coseno.
Ripassa per l’interrogazione sulle funzioni seno e coseno
Sei pronto per l’interrogazione sulle funzioni seno e coseno?
Mettiti alla prova con questi esercizi sui grafici di queste due funzioni!
Sfida sui grafici di seno e coseno
Testo della sfida:
Riesci a capire a quali funzioni i grafici sono associati? Sai anche inserire i valori al posto giusto?
Prova a risolvere la sfida sulle funzioni seno e coseno!


























