Formule di bisezione: seno, coseno, tangente, cotangente
Le formule di bisezione di seno, coseno, tangente e cotangente ti permettono di mettere in relazione un angolo e la sua metà, determinando le funzioni goniometriche di quest’ultima.
Ora che hai studiato le formule di duplicazione, impara a sfruttarle per ricavare e dimostrare le formule di bisezione! Usa anche le formule parametriche razionali del seno e del coseno per risolvere equazioni e disequazioni goniometriche lineari.
In questa lezione imparerai:
- Formula di bisezione del seno: formula, dimostrazione ed esempi;
- Formula di bisezione del coseno: formula, dimostrazione ed esempi;
- Formula di bisezione della tangente e della cotangente: formula, dimostrazione ed esempi;
- Formule parametriche razionali: formula, dimostrazione ed esempi.
- Cosa sono le formule di bisezione
- Tabella formule di bisezione
- Tabella formule parametriche razionali
- Formule di bisezione
- Formule parametriche razionali
- Esercizi sulle formule di bisezione
Cosa sono le formule di bisezione
Le formule di bisezione per le funzioni trigonometriche come seno, coseno, tangente e cotangente sono un insieme di formule utilizzate per calcolare i valori di tali funzioni per angoli dimezzati. Questo metodo prevede di individuare un intervallo in cui si trova la radice dell’equazione e poi dividere ripetutamente tale intervallo a metà finché non si ottiene una soluzione approssimata accettabile.
Le formule di bisezione consentono di determinare le funzioni goniometriche dell’angolo £$\frac{\alpha}{2}$£, in funzione dell’angolo £$\alpha$£. Il seno dell’angolo £$\frac{\alpha}{2}$£, infatti, non è uguale alla metà del seno dell’angolo £$\alpha$£: e lo stesso vale per coseno, tangente e cotangente!
Come si dimostrano le formule di bisezione del seno e del coseno? Bisogna ricorrere alle formule di duplicazione, scrivendo £$\alpha=2\cdot \frac{\alpha}{2}$£.
Per dimostrare le formule di bisezione della tangente e della cotangente, invece, dovrai servirti della seconda relazione fondamentale della goniometria e delle formule di bisezione del seno e del coseno.
Tabella formule di bisezione
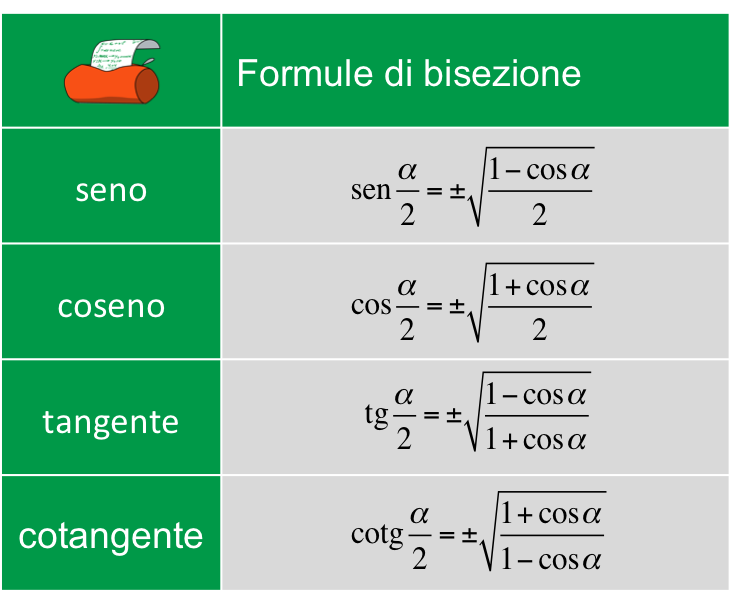
Tabella delle formule di bisezione di seno, coseno, tangente e cotangente.
Tabella formule parametriche razionali
Tabella delle formule parametriche razionali.
Formule di bisezione
Formula di bisezione di seno, coseno, tangente e cotangente:
Formule di bisezione seno, coseno, tangente, cotangente e formule parametriche - Superiori - Galleria
Ecco come dimostrare le formule di bisezione delle funzioni goniometriche. Il metodo è sempre lo stesso: basta vedere l’angolo £$\alpha$£ come £$2\cdot \frac{\alpha}{2}$£ e poi applicare le formule di duplicazione delle funzioni goniometriche.
Formule parametriche razionali
Formule di bisezione seno, coseno, tangente, cotangente e formule parametriche - Superiori - Galleria
Le formule parametriche razionali sono utili per risolvere le equazioni e disequazioni lineari goniometriche.
Si chiamano parametriche perché scriviamo il seno e il coseno dell’angolo £$\alpha$£ in funzione di un parametro £$t=tg \frac{\alpha}{2}$£. Sono razionali perché le scriviamo come rapporto di polinomi.
Esercizi sulle formule di bisezione
Formule di bisezione seno, coseno, tangente, cotangente e formule parametriche - Superiori - Galleria
Prova a risolvere questi esercizi sulle formule di bisezione e sulle forme parametriche razionali delle funzioni goniometriche: così sarai sicuro di essere pronto per l’interrogazione!