Ragionamento matematico: le regole di inferenza e deduzione
Nel campo della matematica e della logica, le regole di inferenza e di deduzione sono strumenti essenziali che guidano il processo di ragionamento e di prova. Queste regole sono il fondamento su cui si basa il ragionamento logico, permettendo di costruire argomentazioni valide e di giungere a conclusioni solide a partire da premesse date.
Le regole di inferenza sono principi che descrivono come si può validamente passare da una o più affermazioni (premesse) a una nuova affermazione (conclusione). Queste regole sono la base della logica deduttiva, dove la verità di determinate premesse garantisce la verità della conclusione. Ad esempio, una regola di inferenza comune è il modus ponens, che afferma che, se abbiamo una premessa “Se P, allora Q" e una seconda premessa “P è vero", possiamo dedurre che “Q è vero".
La deduzione, d’altra parte, è il processo di utilizzo di queste regole di inferenza per costruire catene di ragionamento. In matematica, la deduzione è fondamentale per dimostrare teoremi e risolvere problemi. Partendo da assiomi e definizioni accettati, i matematici utilizzano la deduzione per arrivare a nuove verità matematiche. Questo processo richiede un’attenta applicazione delle regole di inferenza per assicurarsi che ogni passaggio del ragionamento sia valido.
Vediamole!
- Ragionamenti validi o assurdi in matematica
- Regole di deduzione e di inferenza in matematica
- Regole di deduzione e di inferenza: modus Ponens
- Regole di deduzione e di inferenza: modus Tollens
Ragionamenti validi o assurdi in matematica
Un ragionamento è valido quando dalla premessa vera riusciamo ad arrivare ad una conclusione vera.
Ad esempio:
“I girasoli sono fiori. È un girasole, allora è un fiore’’.
Invece consideriamo il seguente esempio:
“Tutti i gatti sono bianchi. Il mio è un gatto, dunque, è bianco.’’
Sembrerebbe un ragionamento valido almeno formalmente, ma allora, cosa non funziona?
Dato che la premessa non è vera, anche se il ragionamento è corretto, la conclusione è errata: è un ragionamento che porta ad un assurdo.
Regole di deduzione e di inferenza in matematica
Per costruire ragionamenti validi si possono utilizzare delle regole di deduzione:
- Modus Ponens
- Modus Tollens.
Sono chiamate anche regole di inferenza e garantiscono la correttezza di un ragionamento.
Modus Ponens: è una regola di inferenza che convalida la premessa per convalidare la conclusione.
Modus Tollens: è una forma di ragionamento che invalida la conclusione per invalidare la premessa.
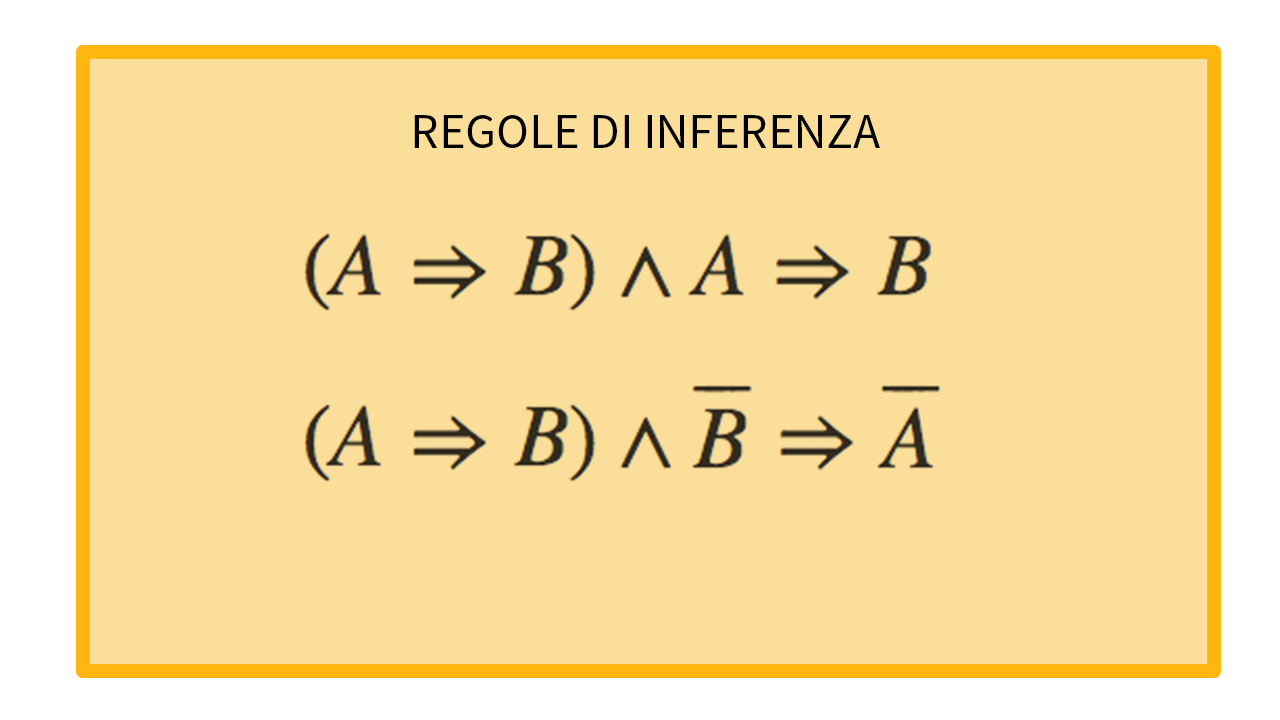
Si scrivono:
£$ (A \Rightarrow B) \wedge A \Rightarrow B$£;
£$ (A \Rightarrow B) \wedge \overline B \Rightarrow \overline A $£.
Regole di deduzione e di inferenza: modus Ponens
Esempio:
‘‘Se hai una Playstation, ti piace giocare ai videogiochi.’’
‘‘Hai una Playstation.’’
“Quindi ti piace giocare ai videogiochi.’’
Modus Ponens: è una regola di inferenza che convalida la premessa per convalidare la conclusione.
Se £$ A \Rightarrow B $£ è vera, ed è vera anche £$A$£, allora £$B$£ è vera.
In simboli: £$ (A \Rightarrow B) \wedge A \Rightarrow B$£.
Ad esempio:
£$A$£“: “Il mio gelato è al cioccolato."
£$B$£: “Metto sempre la panna."
“Se il mio gelato è al cioccolato, allora metto sempre la panna. Il mio gelato è al cioccolato. Quindi metto la panna."
Regole di deduzione e di inferenza: modus Tollens
Consideriamo adesso un altro esempio:
‘‘Se hai una Playstation, ti piace giocare ai videogiochi.’’
‘‘Non ti piace giocare ai videogiochi.’’
‘‘Quindi non hai una Playstation’’
Questo tipo di ragionamento utilizza il Modus Tollens.
Modus Tollens: è una forma di ragionamento che invalida la conclusione per invalidare la premessa.
Se £$A \Rightarrow B$£ è vera, ed è vera anche £$ \overline B $£ , allora £$ \overline A$£ è vera.
In simboli: £$ (A \Rightarrow B) \wedge \overline B \Rightarrow \overline A$£.
Ad esempio:
- £$A$£: “Dal ferramenta ho preso tutto il necessario";
- £$B$£: “Ho tutto quello che serve per riparare l’auto".
“Se dal ferramenta ho preso tutto il necessario, allora ho tutto quello che serve per riparare l’auto. Non ho tutto quello che serve per riparare l’auto, quindi non ho preso dal ferramenta tutto il necessario".
Un altro esempio:
- £$A$£: “Ho finito le carte minori di £$3$£";
- £$B$£: “Ho finito gli assi".
“Se ho finito le carte minori di £$3$£, allora ho finito gli assi. Non ho finito gli assi. Allora non ho finito le carte minori di £$3$£".
