Logaritmi: definizione, formule e proprietà

Agostino Sapienza

INSEGNANTE DI MATEMATICA

Sono nato a Reggio Calabria il 07/10/85. Mi sono diplomato nel 2005 all'Istituto Magistrale Statale Tommaso Gulli. Ho conseguito la laurea triennale in Relazioni Internazionali a Messina e in Economia Internazionale a Padova. Dopo un pò di anni negli studi commercialisti sono stato chiamato per una supplenza covid nella classe di insegnamento A47. Ho poi conseguito l'abilitazione a Trieste nel sostegno e sono entrato di ruolo nel 2023

I logaritmi sono uno strumento matematico essenziale, fondamentale per la comprensione di numerose teorie e applicazioni pratiche in scienza, ingegneria, e informatica. Le proprietà dei logaritmi sono spesso difficili da ricordare. Vuoi capire la dimostrazione di tutte le proprietà?

Prima impariamo qual è la definizione di logaritmo, vediamolo come operazione inversa dell’elevamento a potenza. Vuoi anche sapere come passare da una base all’altra? Qui troverai anche la formula del cambiamento di base!

In questa video lezione imparerai:

Definizione di logaritmo: cosa è il logaritmo, quando esiste, logaritmo e potenze
Proprietà dei logaritmi: proprietà elementari, del prodotto, del quoziente, e della potenza con dimostrazione
Formula del cambiamento di base: come passare da una base ad un’altra in un logaritmo

Definizione di logaritmo
Proprietà dei logaritmi
Formula del cambiamento di base del logaritmo
Interrogazione sui logaritmi
Sfida sui logaritmi!

Definizione di logaritmo

Ma quindi, cos’è precisamente un logaritmo?

Data l’equazione £$a^x=b$£, con £$a>0$£ e £$a$£ diverso da £$1$£, chiamiamo logaritmo in base £$a$£ di £$b$£ l’esponente da dare ad £$a$£ per ottenere £$b$£ e scriviamo: £$x=log_a\,b$£.

Il numero £$a$£ si chiama base del logaritmo, mentre £$b$£ è il suo argomento.

Calcolare il logaritmo (in una certa base) di un numero significa trovare l’esponente che, dato alla base, permette di ottenere quel numero.
Il logaritmo è allora l’operazione inversa dell’elevamento a potenza che permette di ricavare l’esponente!

Abbiamo visto un’altra operazione inversa dell’elevamento a potenza, ovvero l’estrazione di radice, che ci consente di ricavare la base della potenza, cioè di risolvere equazioni del tipo £$x^n=b \Rightarrow x= \sqrt[n]b$£ (con le condizioni opportune su £$n$£ e £$b$£).

Attenzione!
Il logaritmo di numeri negativi non esiste!
Scritture come £$log_{10}(-3)$£ non hanno alcun significato.

Proprietà dei logaritmi

Visto che il calcolo dei logaritmi è l’operazione inversa dell’elevamento a potenza, ci aspettiamo che le proprietà delle potenze ritornino in qualche modo anche nei logaritmi. Vediamone alcune!

PROPRIETÀ DEL PRODOTTO: Il logaritmo di un prodotto è la somma dei logaritmi: £$log_a(b_1 \cdot b_2)=log_ab_1+log_ab_2$£ con le condizioni £$b_1>0 \wedge b_2>0$£.
Per dimostrare questa proprietà applichiamo la definizione di logaritmo, moltiplichiamo membro a membro quello che si ottiene e concludiamo applicando il logaritmo nuovamente.

PROPRIETÀ DEL QUOZIENTE: Il logaritmo di un quoziente è la differenza dei logaritmi: £$log_a \frac{b_1}{b_2}=log_ab_1-log_ab_2$£ con le condizioni £$b_1>0 \wedge b_2>0$£.
Anche per dimostrare questa proprietà partiamo dalla definizione di logaritmo, dividiamo membro a membro le relazioni ottenute e applichiamo i logaritmi ad entrambi i membri per concludere.

PROPRIETÀ DELLA POTENZA: il logaritmo di un numero elevato ad una costante è uguale a quella costante moltiplicata per il logaritmo del numero: £$log_ab^k=klog_a b$£ con la condizione £$b>0$£
Dimostriamo questa proprietà tramite la definizione di logaritmo e di potenza.

PROPRIETÀ ELEMENTARI: il logaritmo di 1 è 0: £$log_a 1=0$£. Il logaritmo in base £$a$£ di £$a$£ è 1: £$log_a\,a=1$£.

Formula del cambiamento di base del logaritmo

È possibile avere le tavole dei logaritmi di tutti i numeri rispetto a tutte le possibili basi?
Sarebbe ovviamente una cosa impossibile! Come se la tua calcolatrice potesse avere infiniti tasti per i logaritmi, uno per ogni possibile base!

Le calcolatrici di solito hanno solo due tasti per i logaritmi:

Il tasto log calcola i logaritmi decimali, cioè quelli con base £$a=10$£
Il tasto ln calcola invece i logaritmi neperiani o naturali, che hanno base £$a=e \sim 2,71828…$£

La base 10 e la base £$e$£ sono le più importanti e le più usate nelle applicazioni.
Basta conoscere i logaritmi in queste basi (anzi, in una sola) per poter ottenere tutti gli altri!
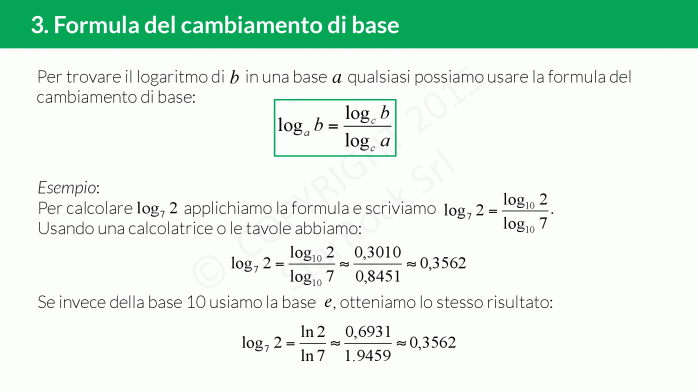
Per trovare il logaritmo di £$b$£ in una base a qualsiasi possiamo usare la formula del cambiamento di base: £$log_ab=\frac{log_cb}{log_ca}$£.