Parallelogrammi e rombi: calcolare perimetro e area
Oggi parleremo di due figure geometriche molto interessanti: i parallelogrammi e i rombi. Entrambi fanno parte della famiglia dei quadrilateri, cioè figure con quattro lati, ma hanno alcune caratteristiche speciali che li rendono unici.
Scopri le proprietà di parallelogrammi e rombi: come possiamo calcolare il loro perimetro e la loro area? Ricorda: non ci sono segreti! Il perimetro di un qualsiasi poligono è sempre uguale alla lunghezza del suo contorno. Il parallelogramma è come un rettangolo storto: sai già come trovare la sua area! L’area di un parallelogramma è uguale a quella di un rettangolo.
Scopri come ricavare la formula dell’area del rombo: dobbiamo partire ancora una volta da un rettangolo.
- Perimetro del parallelogramma e del rombo
- Area del parallelogramma
- Area del rombo
- Formule inverse del parallelogramma e del rombo
Perimetro del parallelogramma e del rombo
Perimetro del parallelogramma

Perimetro del rombo

Il parallelogramma è un quadrilatero che ha i lati uguali e paralleli a due a due. Possiamo trovare il perimetro del parallelogramma come abbiamo imparato a fare per il rettangolo:
P = (b + l) x 2
Il rombo è un parallelogramma con la particolarità di avere tutti e quattro i lati uguali. Possiamo trovare il perimetro del rombo come abbiamo imparato per il quadrato:
P = l + l + l + l = 4 x l
Area del parallelogramma
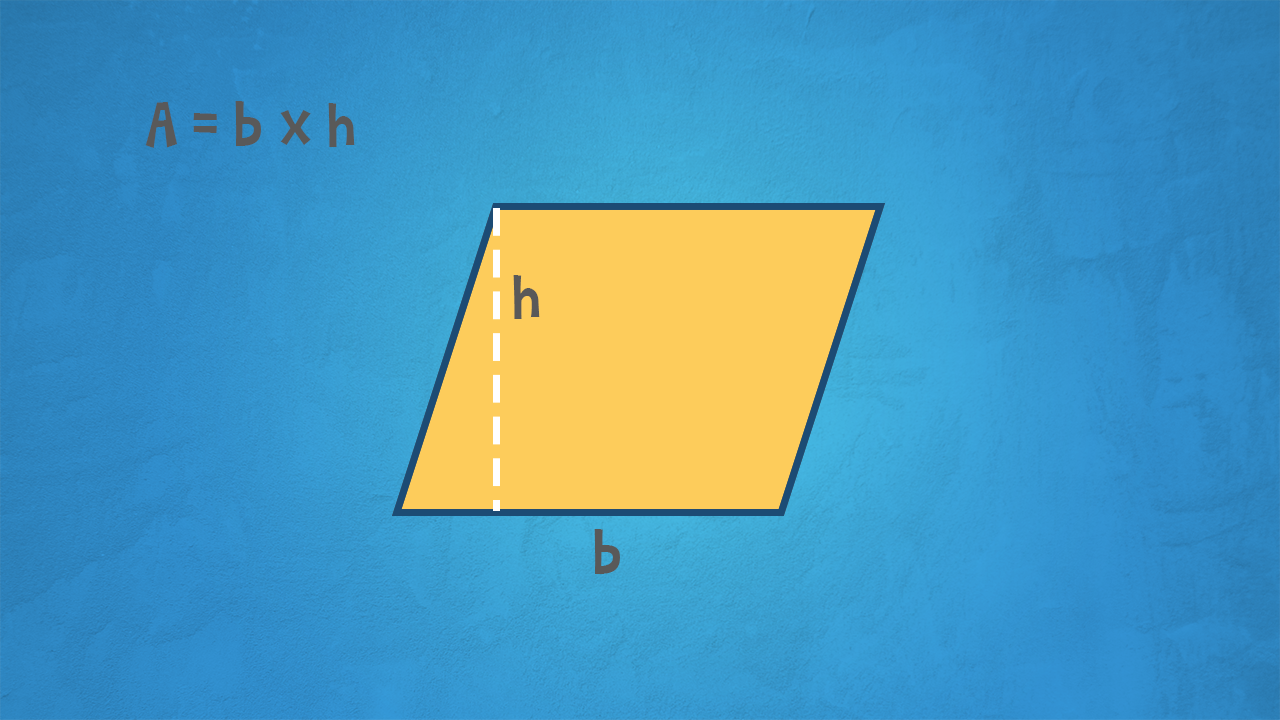
Il parallelogramma non è altro che un rettangolo “storto". Allora possiamo calcolare la sua area come abbiamo imparato per il rettangolo! Se tracciamo l’altezza e “raddrizziamo" il parallelogramma, otteniamo un rettangolo.
L’area del parallelogramma è uguale al prodotto della base per l’altezza:
A = b x h
Ricordati che misuriamo l’area in centimetri quadrati (cm£$^2$£), multipli o sottomultipli.
Area del rombo

Per calcolare l’area di un rombo, abbiamo bisogno di conoscere le sue diagonali. La diagonale di un poligono è quel segmento che collega vertici opposti. Il rombo ne ha due diverse e perpendicolari: le chiamiamo diagonale maggiore (D) e diagonale minore (d).
Disegniamo il rettangolo che ha come lati le due diagonali: riesce a contenere perfettamente il rombo! Com’è però questo rettangolo rispetto al rombo? È esattamente il doppio!
Allora l’area del rombo è uguale alla metà dell’area del rettangolo che ha come lati le due diagonali del rombo.
A = (D x d) : 2
Ricordati che misuriamo l’area in centimetri quadrati (cm£$^2$£).
Formule inverse del parallelogramma e del rombo
È possibile ricavare la misura dei lati di un parallelogramma o delle diagonali di un rombo conoscendo solo il perimetro o l’area? Certo! Basta ricavare le formule inverse, cioè quelle formule che ci permettono di percorrere “all’indietro" la strada fatta per calcolare perimetro e area di un poligono.
Conosciamo il perimetro di un parallelogramma. Sappiamo che è un poligono che ha i lati a due a due uguali e paralleli. Conoscendo una base, possiamo ricavare il lato obliquo e viceversa, come abbiamo imparato a fare con il rettangolo.
l£$_\text{obliquo}$£ = (P£$_\text{parallelogramma}$£ : 2) − b
b = (P£$_\text{parallelogramma}$£ : 2) − l£$_\text{obliquo}$£
Se conosciamo l’area del parallelogramma, possiamo ricavare la base o l’altezza del parallelogramma.
b = A£$_\text{parallelogramma}$£ : h
h = A£$_\text{parallelogramma}$£ : b
Il rombo, come il quadrato, ha quattro lati uguali. Quindi, conoscendo il perimetro, basta dividerlo per 4 e troviamo subito il lato del rombo.
l£$_\text{rombo}$£ = P£$_\text{rombo}$£ : 4
Conoscendo l’area e una delle diagonali di un rombo, possiamo ricavare l’altra diagonale.
D = (A£$_\text{rombo}$£ x 2) : d
d = (A£$_\text{rombo}$£ x 2) : D
