Figure geometriche: isoperimetriche, equiestese e congruenti
Le figure geometriche isoperimetriche, equiestese e congruenti rappresentano tre aspetti interessanti dello studio della geometria, ognuno con le proprie definizioni e proprietà distintive. Le figure isoperimetriche si caratterizzano per avere perimetri uguali, ma possono variare in forma e area. Questo concetto si collega al problema isoperimetrico, che indaga quale figura possa contenere l’area massima dato un perimetro fisso, con il cerchio che spesso emerge come la soluzione ottimale in un contesto bidimensionale.
Le figure equiestese, invece, si concentrano sull’uguaglianza delle aree. Diverse figure geometriche possono avere la stessa area pur differendo significativamente nella forma, nel perimetro e in altre caratteristiche geometriche. Questa proprietà evidenzia la varietà di modi in cui uno spazio bidimensionale può essere configurato e occupato, indipendentemente dalla similitudine esterna delle forme.
Infine, le figure congruenti introducono un concetto di equivalenza basato sulla forma e sulle dimensioni. Due figure sono congruenti se una può essere trasformata nell’altra attraverso una serie di traslazioni, rotazioni o riflessioni, mantenendo invariati tutti gli angoli interni e le lunghezze dei lati. La congruenza sottolinea una corrispondenza esatta tra figure in termini di forma e dimensione, indipendentemente dalla loro posizione o orientamento nello spazio.
Vediamoli meglio.
- Cosa sono le figure isoperimetriche
- Cosa sono le figure equiestese
- Cosa sono le figure congruenti
- Esercizi sulle figure isoperimetriche, equiestese e congruenti
Cosa sono le figure isoperimetriche
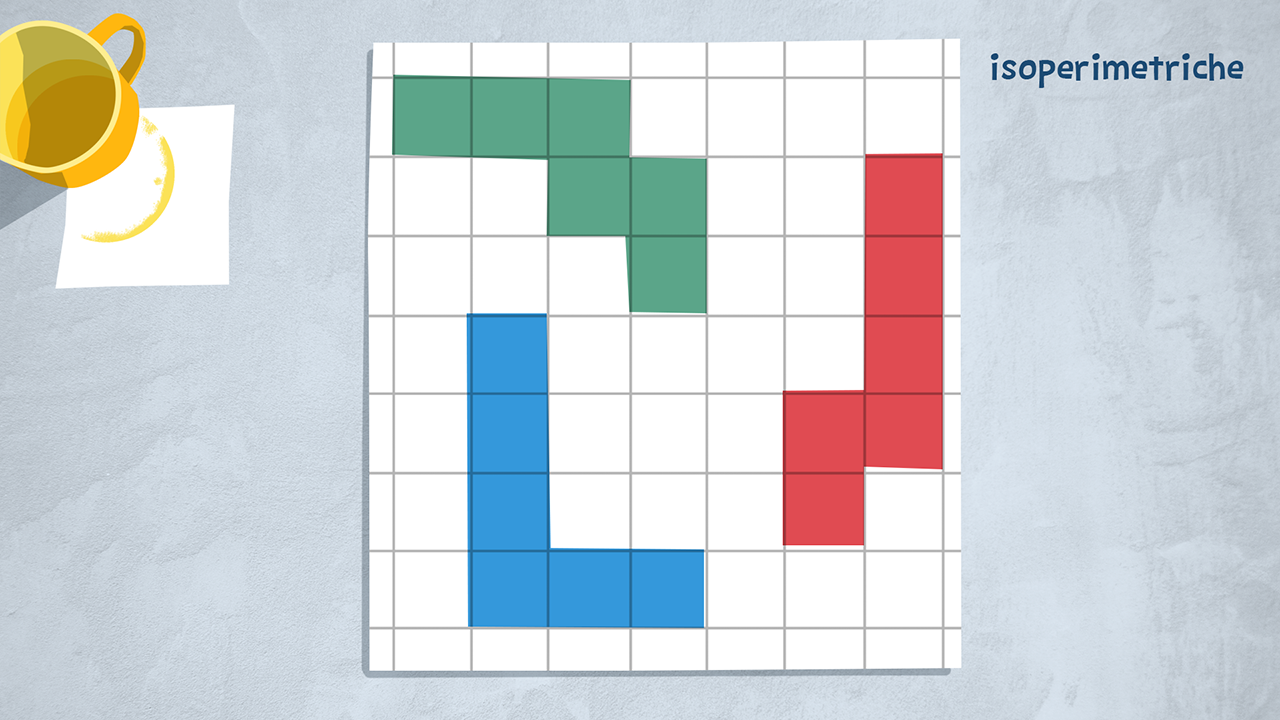
Due figure che hanno lo stesso perimetro si dicono isoperimetriche. Non importa la forma che hanno questi poligoni, se misuriamo la lunghezza del loro perimetro, troviamo lo stesso risultato.
Osserva le figure nell’immagine: sono isoperimetriche?
Le figure isoperimetriche si definiscono attraverso la loro caratteristica comune di avere perimetri uguali. Questo termine deriva dal famoso problema isoperimetrico in geometria, che cerca di determinare quale figura possieda l’area massima data la condizione di un perimetro fisso. Questa indagine porta spesso al cerchio come la soluzione ottimale nel contesto bidimensionale, sottolineando l’interessante interazione tra la forma di una figura e lo spazio che essa può racchiudere.
Cosa sono le figure equiestese
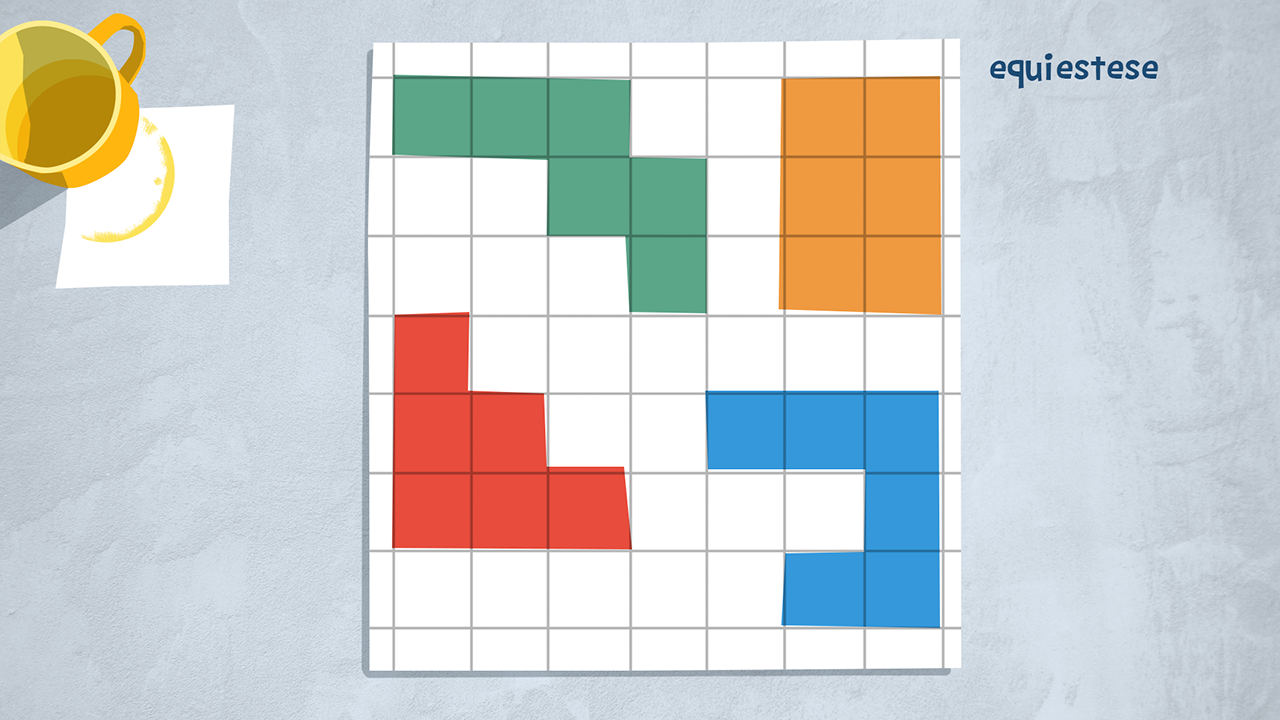
Due figure che hanno lo stessa area si dicono equiestese o equivalenti. Non importa la forma che hanno questi poligoni, se misuriamo la loro superficie, troviamo lo stesso risultato.
Ma cos’è l’area o la superficie di un poligono? È la parte di piano che racchiude il suo contorno: scopriremo presto come misurare l’area di un poligono. Per le figure, come quelle che vedi nell’immagine, basta contare il numero di quadretti che sono all’interno del perimetro.
Osserva le figure nell’immagine: sono equiestese?
Questa proprietà mette in luce la flessibilità e la diversità delle configurazioni geometriche nel riempire uno spazio bidimensionale equivalente. L’esplorazione delle figure equiestese amplia la comprensione di come diverse forme possano occupare lo stesso “volume" geometrico, pur presentando contorni e caratteristiche esterne notevolmente differenti.
Cosa sono le figure congruenti
Osserva le figure nell’immagine: che cos’hanno in comune? Se provassimo a ritagliarle, riusciremmo a sovrapporle perfettamente. Sono figure congruenti!
I poligoni congruenti sono equiestesi e isoperimetrici, hanno la stessa forma perché possiamo sovrapporli perfettamente.
Due figure sono considerate congruenti se una può essere trasformata nell’altra attraverso movimenti rigidi come traslazioni, rotazioni o riflessioni, senza alterare le dimensioni o gli angoli interni. La congruenza enfatizza una corrispondenza esatta in termini di forma e dimensioni, indipendentemente dalla posizione o dall’orientamento delle figure nello spazio, evidenziando un senso di identità geometrica pura tra le forme.
Esercizi sulle figure isoperimetriche, equiestese e congruenti
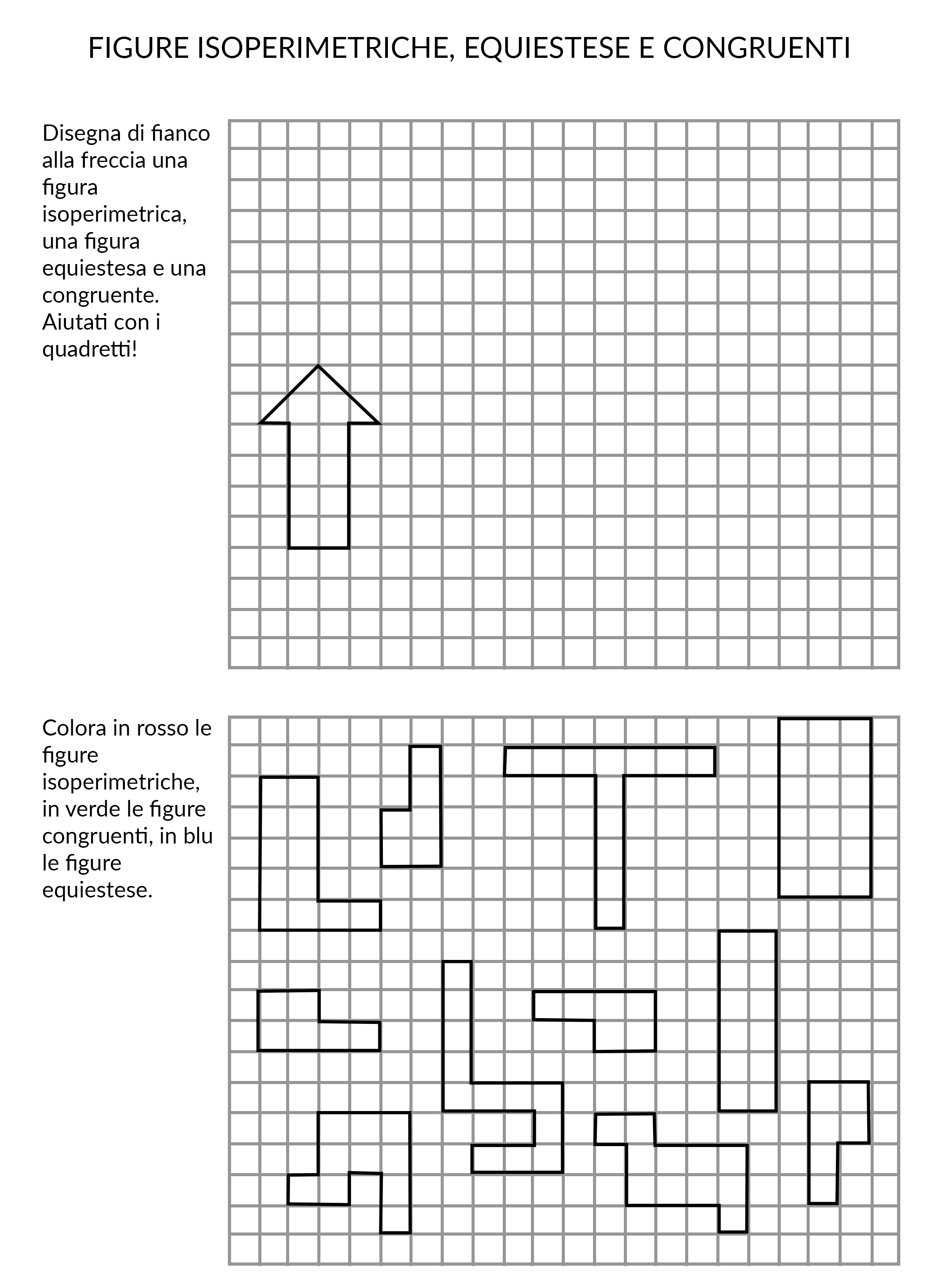
Ecco una scheda per esercitarsi un po’ con le figure isoperimetriche e le figure equiestese: .
Provate a fare disegnare sul quaderno figure diverse: poligoni equiestesi, ma non isoperimetrici; poligoni isoperimetrici, ma non equiestesi; poligoni congruenti, cioè sia equiestesi che isoperimetrici.