Perimetro e area di triangoli: come calcolarli
I triangoli sono figure geometriche con tre lati e tre angoli. Imparare a conoscere i triangoli è molto divertente perché li possiamo trovare ovunque intorno a noi, come nei tetti delle case, nei segnali stradali e persino nelle montagne! Esistono diversi tipi di triangoli, ognuno con le proprie caratteristiche speciali.
Ricordi tutti i triangoli che abbiamo imparato a classificare? Ora scopri come calcolare perimetro e area dei triangoli isosceli, equilateri, scaleni… chi più ne ha più ne metta!
Com’è possibile calcolare l’area di un poligono così strano come il triangolo? Cerchiamo sempre di ricondurci ad un parallelogramma! Infatti, se proviamo ad unire due triangoli, di qualsiasi tipo, otteniamo un parallelogramma! È presto fatto: l’area di un triangolo è la metà di quella di un parallelogramma con la stessa base e la stessa altezza.
- Perimetro del triangolo
- Area del triangolo
- Formule inverse del triangoli
- Scopri il segreto della formula dell'area del triangolo
Perimetro del triangolo
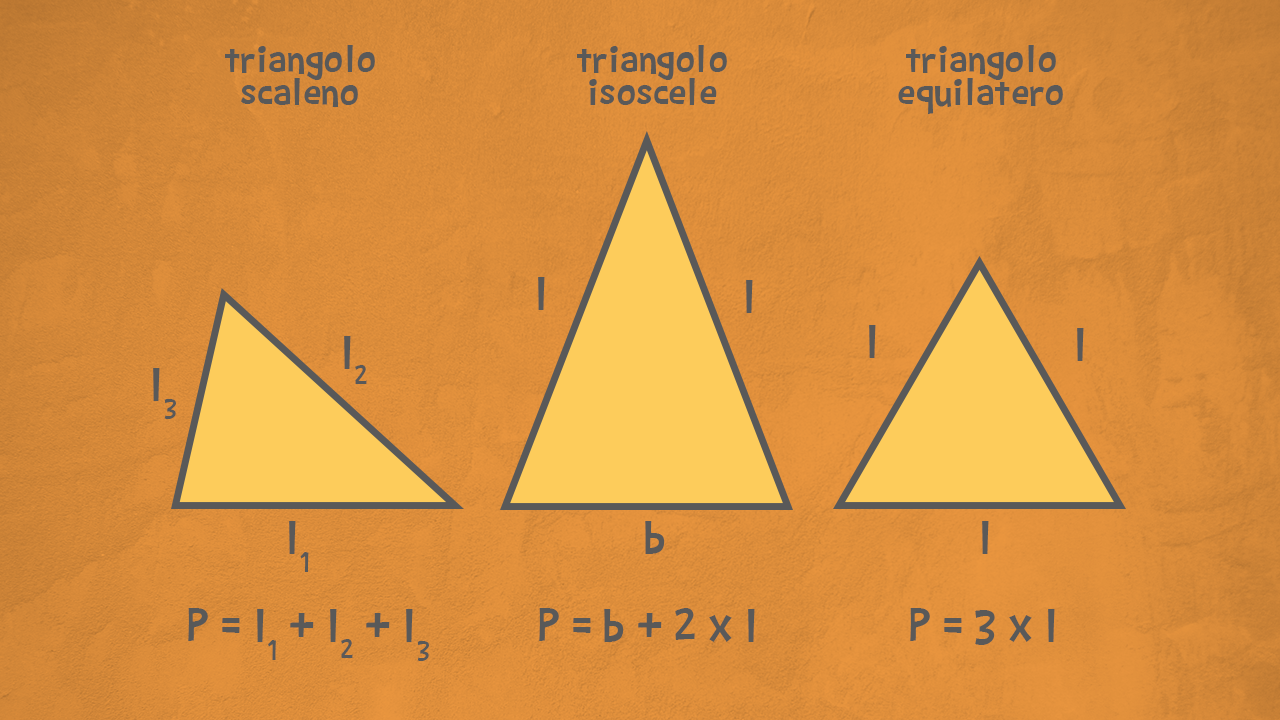
Un triangolo è il poligono più semplice che possiamo disegnare: un poligono con tre lati. Abbiamo imparato a classificare i triangoli in base ai lati e in base agli angoli: conosciamo il triangolo scaleno, isoscele e equilatero, poi il triangolo acutangolo, rettangolo e ottusangolo.
Non importa quale triangolo abbiamo davanti: il perimetro è sempre la misura del contorno del poligono. Ci basta quindi sommare le misure dei tre lati del triangolo per trovare il perimetro:
P = l£$_1$£ + l£$_2$£ + l£$_3$£
Per il perimetro di un triangolo isoscele, in cui riconosciamo la base (b) e due lati uguali (l), la formula si semplifica:
P = b + 2 x l
Il caso più semplice è ovviamente il perimetro del triangolo equilatero che ha tutti e tre i lati uguali:
P = 3 x l
Area del triangolo
Il triangolo è diverso da tutte le altre figure che abbiamo studiato finora. Ha solo tre lati! Come possiamo calcolare la sua area?
Proviamo a lavorare sul triangolo per ricondurci a una qualche forma che conosciamo già. Se prendiamo due triangoli e li mettiamo uno di fianco all’altro, cosa riusciamo a disegnare? Un parallelogramma: ha i lati paralleli a due a due e la base è uguale quella del triangolo.
Disegniamo l’altezza del triangolo e possiamo usare la formula che abbiamo imparato per il parallelogramma, ricordandoci però di dividere per 2. Calcoliamo l’area di un triangolo così:
A = [b x h] : 2
Nell’esempio abbiamo unito due triangoli rettangoli e abbiamo trovato un rettangolo, ma possiamo fare lo stesso giochino con tutti i triangoli: otterremo un parallelogramma generico!
Ricordati che misuriamo l’area in centimetri quadrati (cm£$^2$£), multipli o sottomultipli.
Formule inverse del triangoli
Ci saranno problemi in cui viene fornito il perimetro o l’area di un triangolo e dobbiamo riuscire a ricavare delle informazioni: la lunghezza del lato o dell’altezza. Come possiamo fare? Utilizzando le formule inverse.
Conosciamo il perimetro di un triangolo equilatero. Come facciamo a trovare la misura del suo lato? Dividiamo il perimetro per 3.
l = P : 3
Per gli altri triangoli, invece, non possiamo fare lo stesso ragionamento: occorrono almeno due informazioni per il triangolo isoscele e tre informazioni per quello scaleno, che ha tutti i lati diversi. Vediamo un paio di formule per il triangolo isoscele:
l = (P – b) : 2
b = P – (2 x l)
Per quanto riguarda invece l’area, possiamo ricavare la base o l’altezza, a seconda dei dati che abbiamo a disposizione.
b = (2 x A) : h
h = (2 x A) : b
Scopri il segreto della formula dell’area del triangolo
Scopri il segreto della formula dell’area del triangolo.
Basta prendere due triangoli, metterli uno di fianco all’altro e… ecco un parallelogramma! Ricordi come si calcola l’area di un parallelogramma? Ecco, il nostro triangolo corrisponde proprio alla metà di quel parallelogramma.
Prendi spunto da questa scheda per dimostrare come calcolare l’area di un triangolo: