Quadrati e rettangoli: come calcolare area e perimetro
Il calcolo dell’area e del perimetro di rettangoli e quadrati è uno degli aspetti fondamentali della geometria piana, che fornisce gli strumenti per comprendere e quantificare lo spazio e le dimensioni di queste figure. Il rettangolo, caratterizzato da quattro lati e angoli retti, con lati opposti paralleli e uguali, e il quadrato, un caso particolare di rettangolo con tutti e quattro i lati uguali, sono tra le forme più comuni e basilari in geometria.
L’area di una figura geometrica rappresenta la quantità di spazio bidimensionale all’interno dei suoi confini. Il perimetro, d’altra parte, misura la lunghezza totale del contorno di una figura.
Vediamo passo per passo come fare.
- Come calcolare il perimetro del rettangolo e del quadrato
- Come calcolare l'area del rettangolo
- Come calcolare l'area del quadrato
- Formule inverse dell'area di quadrati e rettangoli
- Esercizi su perimetri e aree di quadrati e rettangoli
Come calcolare il perimetro del rettangolo e del quadrato
Perimetro del rettangolo

Perimetro del quadrato

Il rettangolo è un quadrilatero con i lati uguali a due a due. Come sempre, per calcolare il suo perimetro, ci basta sommare le misure dei suoi lati. Riusciamo a distinguere una base (b), il lato su cui “poggia" il rettangolo, e un’altezza (h), il lato verticale. Possiamo trovare il perimetro di un rettangolo così:
P = (b + h) x 2
Il quadrato è un rettangolo particolare perché ha 4 lati tutti uguali. Per calcolare il perimetro del quadrato è dato dalla somma delle misure dei suoi quattro lati. Se indichiamo i lati con la lettera l, quindi, possiamo trovare facilmente il perimetro del quadrato:
P = l + l + l + l = 4 x l
Come calcolare l’area del rettangolo
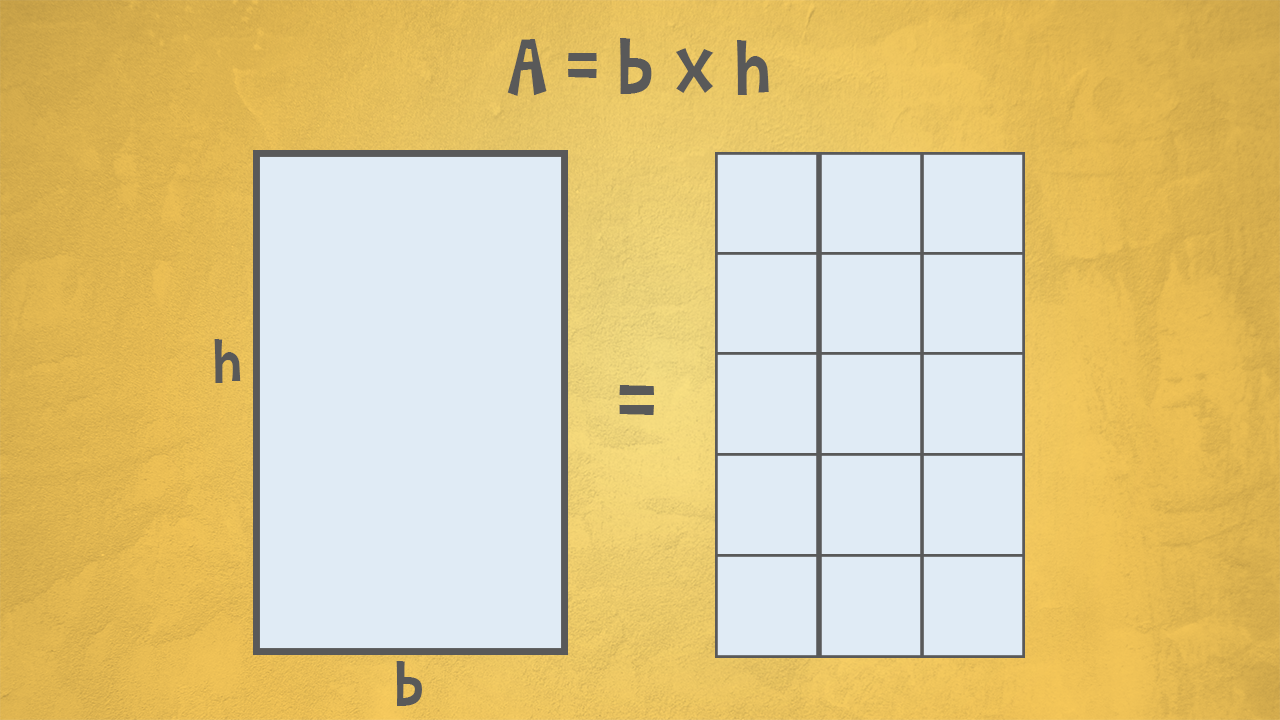
Qual è l’area di un rettangolo con la base di 3 cm e l’altezza di 5 cm?
Osserviamo il rettangolo e dividiamolo in quadretti tutti uguali. Con quanti quadretti riusciamo a ricoprirlo? Prendiamo dei quadratini con il lato di 1 cm: ce ne stanno ben 15, cioè 5 righe da 3 quadretti ciascuna.
L’area del rettangolo è uguale al prodotto della base per l’altezza!
A = b x h
Ricordati che misuriamo l’area in centimetri quadrati (cm£$^2$£), multipli o sottomultipli. È proprio come contare i quadratini con il lato di 1 cm che stanno nel rettangolo!
Come calcolare l’area del quadrato
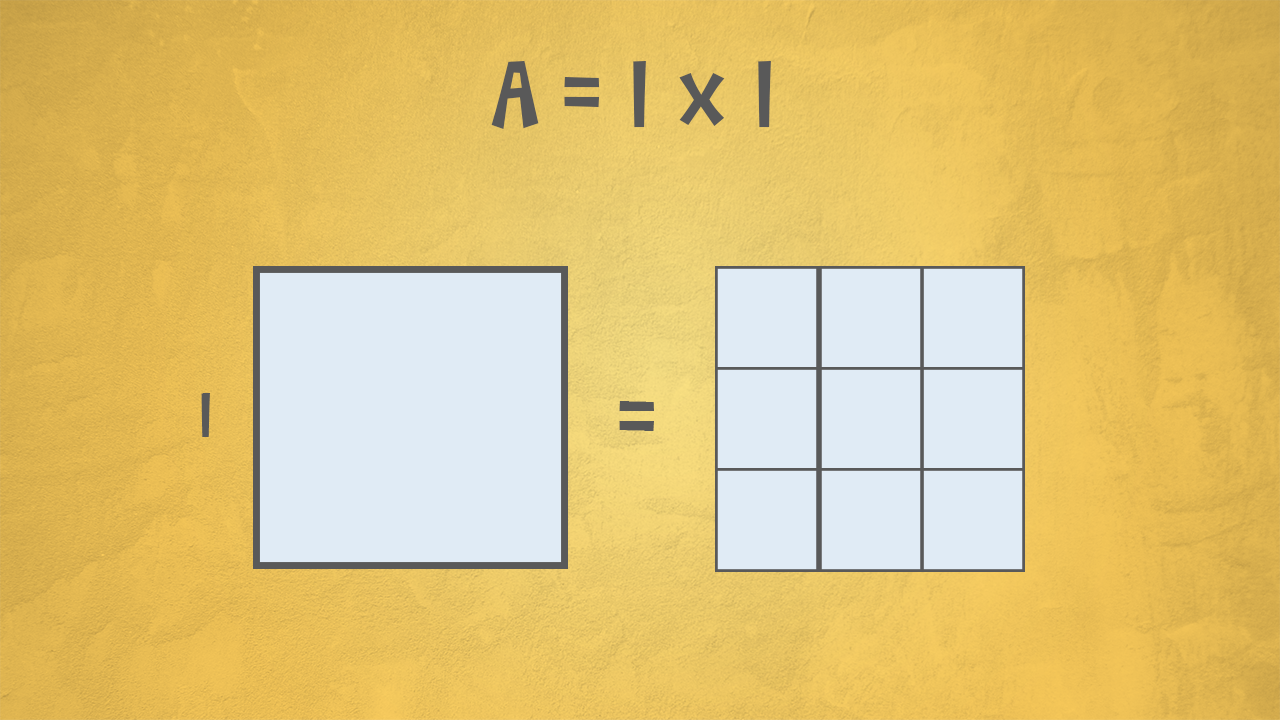
Abbiamo già detto che il quadrato è un rettangolo particolare, quindi non dobbiamo imparare niente di nuovo per calcolare l’area del quadrato.
Qual è l’area di un quadrato con il lato di 3 cm?
Dividiamolo in quadretti tutti uguali, con il lato di 1 cm: ce ne stanno 9 in tutto, cioè 3 righe da 3 quadretti ciascuna.
L’area del quadrato è uguale al prodotto del lato per se stesso, cioè al lato alla seconda:
A = l x l = l£$^2$£
Ricordati che misuriamo l’area in centimetri quadrati (cm£$^2$£), multipli o sottomultipli. È proprio come contare i quadratini con il lato di 1 cm che stanno nel quadrato!
Formule inverse dell’area di quadrati e rettangoli
Come facciamo a risolvere i problemi in cui non sono indicate le misure dei lati di quadrati o rettangoli, ma solo il perimetro o l’area? Utilizziamo le formule inverse!
Sappiamo il perimetro del quadrato, come facciamo a trovare la misura del suo lato? Ricorda che il quadrato ha quattro lati uguali, quindi basta una divisione:
l = P : 4
E che ne dici del rettangolo? Come facciamo a trovare la misura della base conoscendo solo perimetro e altezza? O la misura dell’altezza conoscendo solo perimetro e base? Basta una divisione e poi una sottrazione:
b = (P : 2) – h
h = (P : 2) – b
Conosciamo l’area di un rettangolo e la sua base. Come facciamo a trovare l’altezza? O viceversa, conosciamo l’altezza: come facciamo a trovare la base?
h = A : b
b = A : h
Tieni a mente le formule inverse per poter risolvere tutti i problemi di geometria con quadrati e rettangoli.
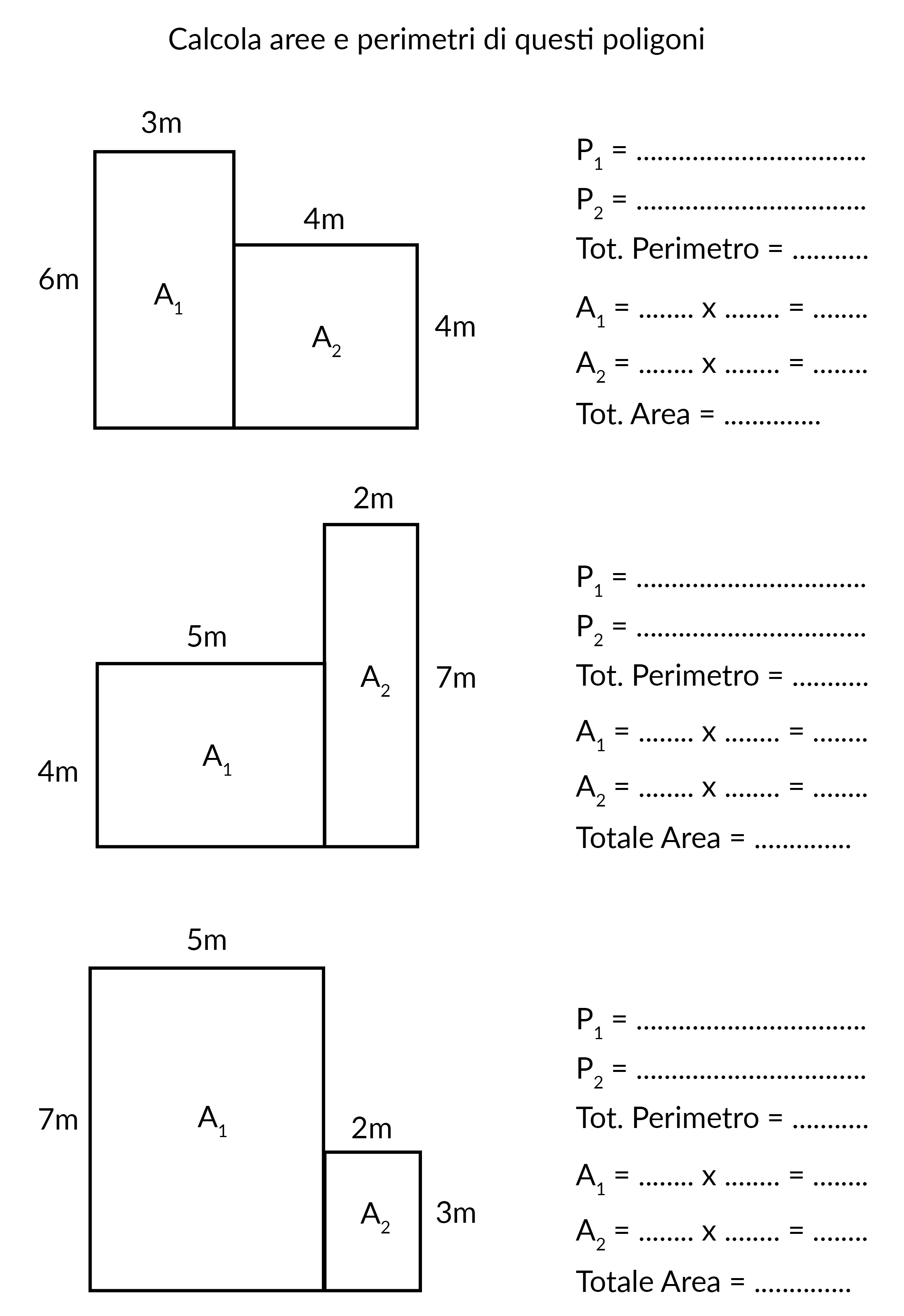
Esercizi su perimetri e aree di quadrati e rettangoli
Ecco un paio di schede per provare ad affrontare esercizi diversi sul calcolo del perimetro e dell’area di quadrati e rettangoli. Scarica i pdf!