Come passare dal numero decimale alla frazione e viceversa

I numeri decimali e le frazioni possono sembrare molto diversi tra loro, ma in realtà sono strettamente correlati e potremmo anche considerarli come simili, per certi versi.

Le frazioni possono essere scritte come numeri decimali finiti o decimali infiniti periodici dividendo il numeratore per il denominatore. Sei quindi pronto a studiare cosa è un numero decimale finito e quando un numero decimale è periodico semplice o periodico misto e come si passa dalla frazione ai numeri con la virgola.

E se vogliamo passare da un numero con la virgola ad una frazione? Ci vengono in aiuto le frazioni generatrici, diverse a seconda che il numero decimale sia finito, periodico semplice o periodico misto!

E cosa sono i numeri irrazionali e reali? Con questa lezione concludiamo lo studio degli insiemi numerici!

Pronti? Iniziamo!

Vuoi metterti alla prova? Tenta il nostro quiz!

• Le regole per convertire una frazione in un numero decimale e viceversa
• Numeri decimali finiti e periodici
• Qual è il legame tra frazione e numero decimale?
• Come passare dalla frazione al numero decimale
• Frazione generatrice
• Come passare dal numero decimale alla frazione
• Frazioni non decimali
• Numeri irrazionali e numeri reali
• Interrogazione su frazioni e decimali
• Sfida: frazioni e decimali

Le regole per convertire una frazione in un numero decimale e viceversa

Il passaggio da un numero decimale a una frazione può sembrare complicato, ma in realtà segue alcune regole precise. Innanzitutto, è importante capire che la posizione di una cifra dopo il punto decimale, cioè la virgola, indica in realtà una frazione di una certa potenza di 10. Ad esempio, la cifra 3 in 0.3 rappresenta £$\frac{3}{10} $£, mentre la cifra 3 in 0.03 rappresenta £$\frac{3}{100} $£. Per convertire un numero decimale in una frazione, dobbiamo quindi esprimere il numero come una frazione di una potenza di 10.

D’altro canto, per convertire una frazione in un numero decimale, possiamo dividere il numeratore per il denominatore. Per esempio, la frazione £$\frac34$£ può essere convertita in un numero decimale eseguendo la divisione £$3 ÷ 4$£, che dà come risultato£$ 0,75$£. Se la divisione non si conclude, otteniamo un numero decimale periodico, che può essere espresso con un punto o una linea sopra le cifre che si ripetono.

Ma non preoccuparti, adesso andremo ancora di più nel dettaglio!

Numeri decimali finiti e periodici

Numeri decimali finiti

Numeri decimali periodici

Le frazioni possono essere scritte come numeri decimali finiti o numeri decimali periodici, basta fare la divisione tra numeratore e denominatore. Se il risultato di questa divisione è un numero intero o un numero con la virgola che ha un numero di cifre dopo la virgola finito allora hai trasformato la frazione in un numero decimale finito, se invece il numero di cifre dopo la virgola è infinito la frazione è diventata:

• un numero decimale periodico semplice, cioè un numero le cui infinite cifre dopo la virgola si ripetono, chiamate periodo, come per esempio il numero £$\frac{1}{3}=0,33333=0,\bar3$£;
• un numero decimale periodico misto, come per esempio il numero £$\frac{5}{6}=0,83333=0,8\bar3$£, cioè un numero che dopo la virgola ha alcune cifre che non si ripetono, e questa parte è chiamata antiperiodo, seguite da cifre che si ripetono.

Qual è il legame tra frazione e numero decimale?

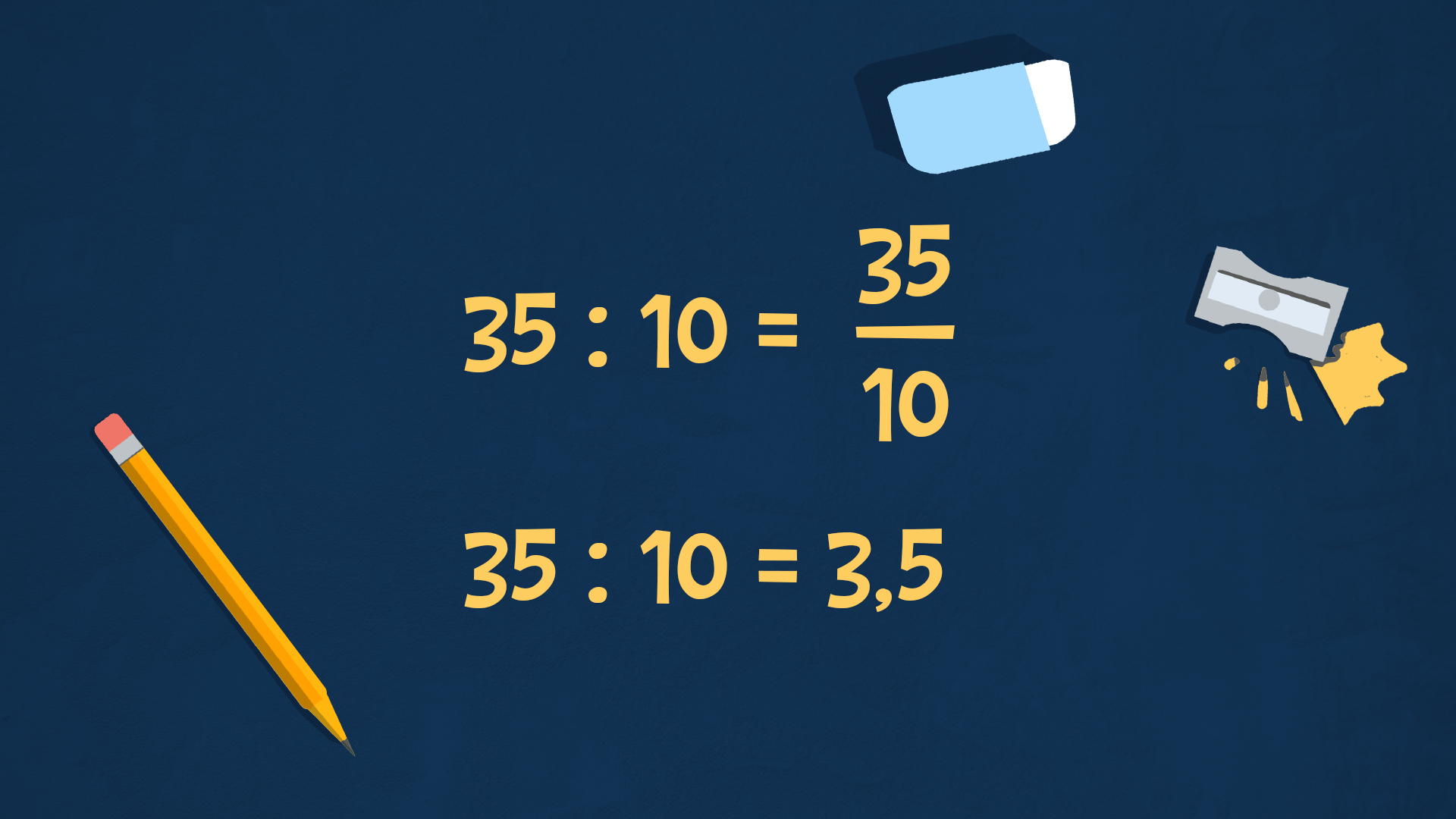
La frazione è un modo diverso per scrivere una divisione, indicando i due termini della divisione separati da una linea di frazione. I numeri decimali, come abbiamo imparato, possono essere risultati di divisioni non esatte.

Allora possiamo scrivere i numeri decimali sotto forma di frazioni. Scopriamo come farlo!

Come passare dalla frazione al numero decimale

Per individuare il numero decimale corrispondente ad una frazione, basta risolvere la divisione “numeratore : denominatore" e trovare il risultato.

Iniziamo ad analizzare le frazioni decimali, cioè quelle frazioni che hanno come denominatore 10, 100 o 1000. In questi casi è semplice individuare il numero decimale corrispondente: sappiamo che per dividere per 10, 100 o 1000 basta spostare la virgola a sinistra di una, due o tre posizioni.

£$ \dfrac{631}{100} = $£ 631 : 100 = 6,31

In generale però non è sempre così semplice. Non tutte le frazioni sono decimali, ma il procedimento per individuare il numero decimale corrispondente è sempre lo stesso: calcolare la divisione.

£$ \dfrac{82}{40} = $£ 82 : 40 = 2,05

Frazione generatrice

Abbiamo visto come trasformare una frazione in un numero decimale. Ora vogliamo fare il contrario: se hai un numero decimale finito o periodico, qual è la sua frazione generatrice?

Caso 1. Numero decimale finito:

• numeratore: il numero moltiplicato per la potenza di £$10$£ avente come esponente il numero delle cifre dopo la virgola
• denominatore: la potenza di £$10$£ avente come esponente il numero delle cifre dopo la virgola

Caso 2. Numero decimale infinito periodico semplice:

• numeratore: la differenza tra il numero senza la virgola e il numero formato dalla parte intera
• denominatore: il numero formato da tanti £$9$£ quante sono le cifre del periodo

Caso 3: Numero decimale infinito periodico misto:

• numeratore: la differenza tra il numero senza la virgola e il numero formato da tutte le cifre che precedono il periodo (parte intera e antiperiodo)
• denominatore: il numero formato da tanti £$9$£ quante sono le cifre del periodo seguiti da tanti [iol_placeholder type="formula" engine="katex" display="inline"/] quante sono le cifre dell’antiperiodo

Come passare dal numero decimale alla frazione

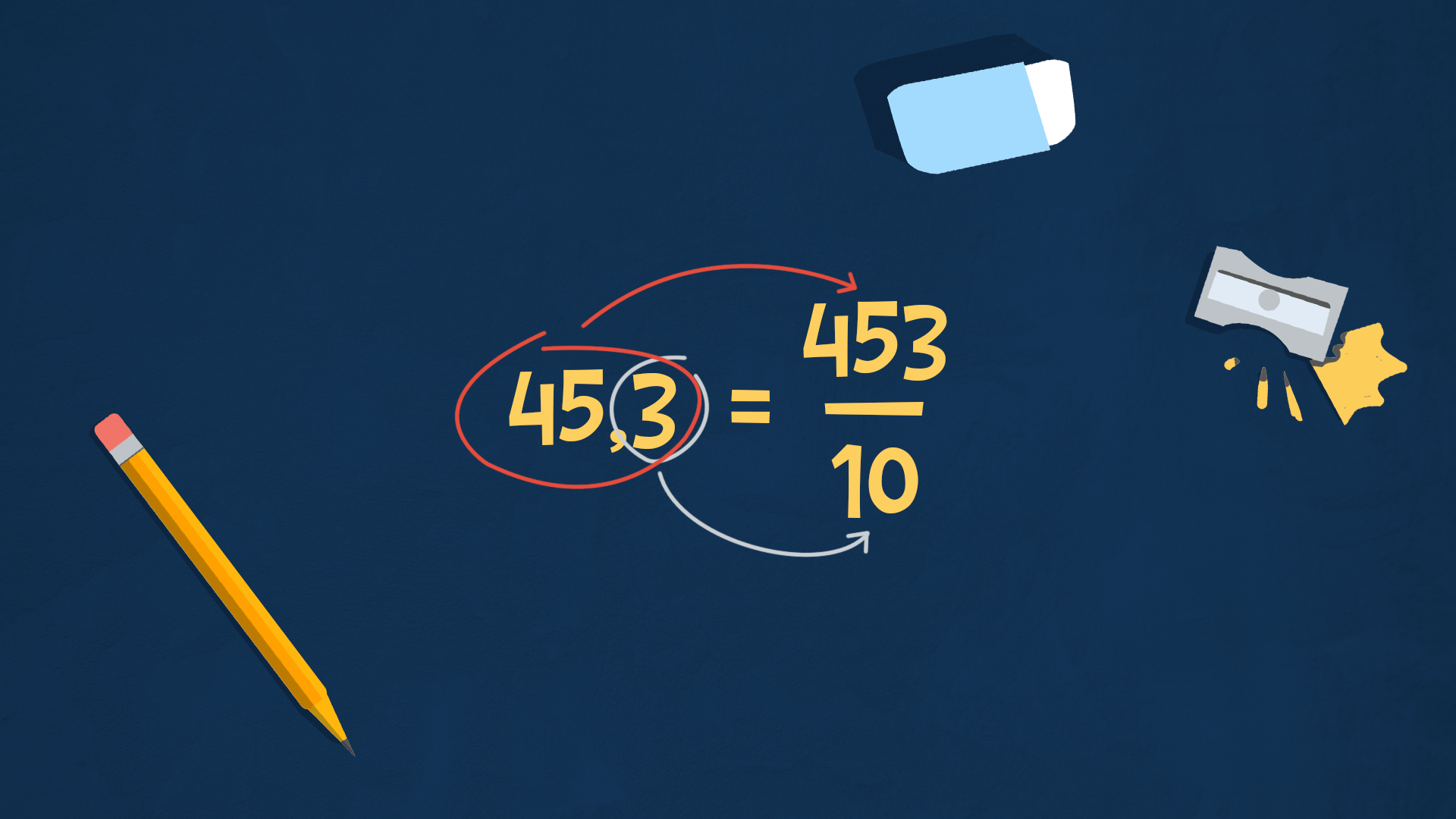
Per individuare la frazione associata a ciascun numero decimale, basta leggere bene il numero: 45,3 ha una sola cifra dopo la virgola, quindi raggiunge i decimi

La frazione corrispondente ad un numero decimale ha come numeratore il numero scritto senza virgola e come denominatore un 1 seguito da tanti zeri quante sono le cifre dopo la virgola.

Allora 45,3 £$ = \dfrac{453}{10} $£

Infatti, se noi risolviamo la divisione 453 : 10 otteniamo proprio 45,3.

Quale frazione corrisponde al numero 3,021?

Frazioni non decimali

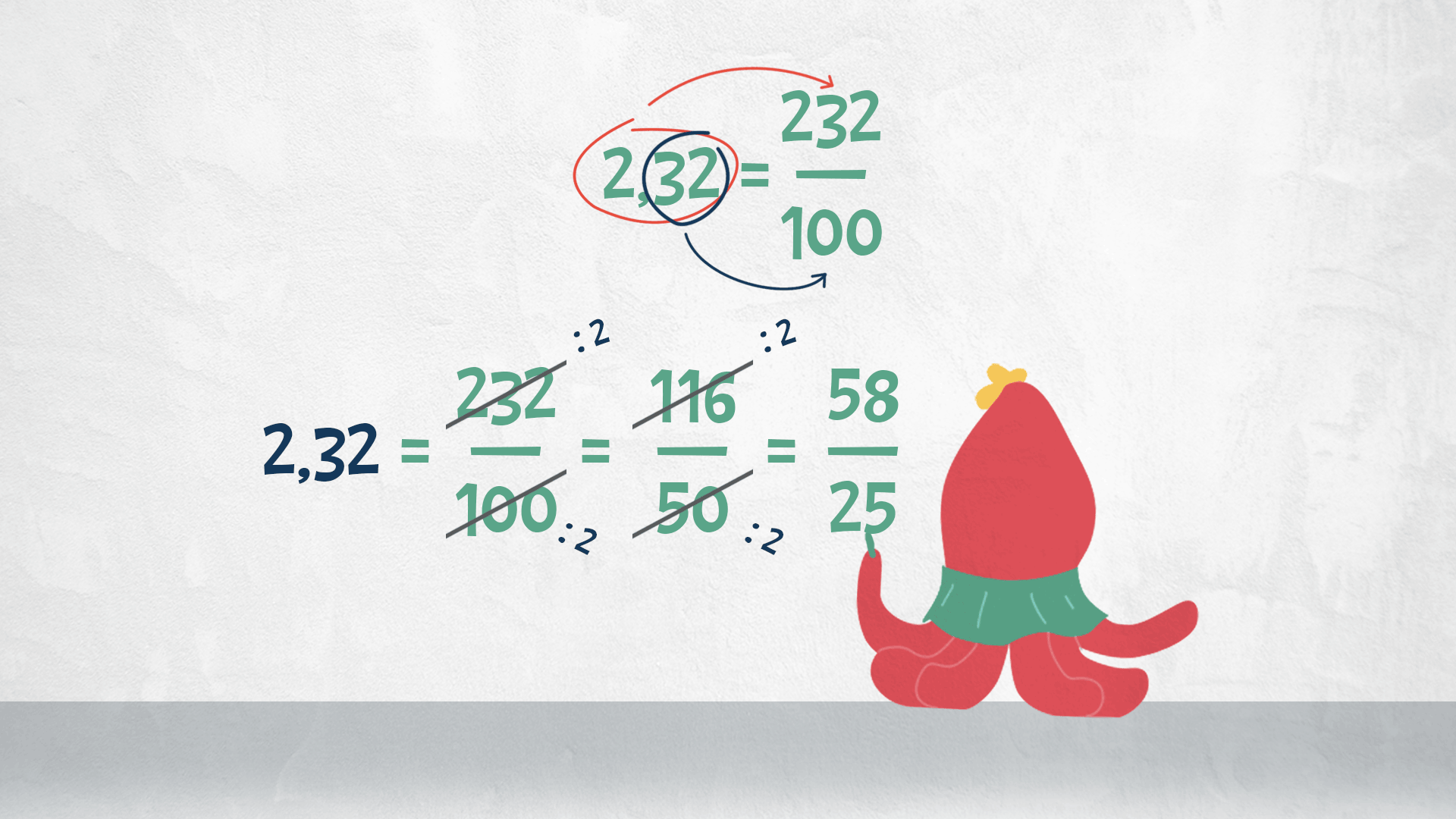
Riusciamo a trovare anche una frazione non decimale? Per esempio: qual è la frazione corrispondente al numero 2,32?

Procediamo come abbiamo imparato: 2,32 £$ = \frac{232}{100} $£. Visto che numeratore e denominatore sono numeri pari, possiamo semplificare dividendo entrambi per 2.

£$ \dfrac{232}{100} = \dfrac{116}{50} = \dfrac{58}{25} $£

Possiamo concludere quindi che 2,32 £$ = \dfrac{58}{25} $£.

Questa è una frazione non decimale, cioè che non ha come denominatore 10 o una potenza di 10. Inoltre è una frazione ridotta ai minimi termini, cioè che non possiamo semplificare ulteriormente perché numeratore e denominatore non hanno divisori in comune.

Viceversa, se abbiamo una frazione non decimale, possiamo trovare facilmente il numero decimale corrispondente risolvendo la divisione.

£$ \dfrac 38 = $£ 3 : 8 = 0,375

Da qui possiamo ricavare la frazione decimale equivalente a £$ \dfrac 38 $£, come abbiamo già imparato a fare: 0,375 £$ = \dfrac{375}{1000} $£.

Numeri irrazionali e numeri reali

Fino ad ora hai studiato l’insieme dei numeri razionali £$\mathbb{Q}$£ che contiene l’insieme dei numeri interi £$\mathbb{Z}$£ che a sua volta contiene l’insieme dei numeri naturali £$\mathbb{N}$£.

In questo video scoprirai l’insieme dei numeri irrazionali, cioè quei numeri decimali con infinite cifre dopo la virgola che non possono essere scritti come rapporto tra due numeri interi, cioè non possono essere scritti come una frazione!
Per concludere vedrai che l’insieme che contiene l’insieme dei numeri razionali e irrazionali è quello dei numeri reali £$\mathbb{R}$£!

Interrogazione su frazioni e decimali

Ecco una simulazione di quella che potrebbe essere l’interrogazione di domani! Se non hai ancora compreso cos’è un numero decimale finito o periodico, che cos’è la frazione generatrice, un numero irrazionale o reale riguardati i video o leggi bene la spiegazione degli esercizi!

Sfida: frazioni e decimali

Sfida:

Soluzione:

Una bottiglia di succo di frutta da un litro da dividere in £$4$£ o £$6$£ bicchieri, come fare? Se non sai come risolvere subito la sfida allenati guardando i video e facendo gli esercizi sulle frazioni e i decimali! Vedrai che leggendo bene le spiegazioni degli esercizi sarà facilissimo risolvere la sfida!