I numeri naturali: addizione e sottrazione
La matematica non può fare a meno dei numeri! I numeri più facili da imparare sono i numeri naturali, cioè tutti quelli senza la virgola, più grandi di 0. Ma anche lo 0 è un numero naturale…
Ma oltre a contare, cos’altro possiamo fare con i numeri naturali? Beh, già contando facciamo un’operazione. Stiamo aggiungendo 1 a un numero. L’operazione “aggiungere" viene chiamata addizione.
E se invece contassimo all’indietro? Invece di aggiungere, stiamo “togliendo" un numero alla volta. Questa operazione si chiama sottrazione. Sembra facile? Certo che lo è, ma conosci anche le proprietà di queste operazioni?
Non farti intimidire da addizione e sottrazione: impara le proprietà delle operazioni per fare i calcoli più velocemente! Scopri l’elemento neutro dell’addizione e quando non è possibile calcolare una differenza tra due numeri.
Quanto fa 5 + 0? E 0 + 3? Il risultato non cambia: lo 0 è l’elemento neutro dell’addizione!
Scopri come velocizzare i calcoli quando svolgi un’addizione o una sottrazione, grazie alle loro proprietà. Guarda i video, segui gli esempi e gli esercizi svolti, e allenati per testare la tua conoscenza sull’addizione e la sottrazione di numeri naturali.
- Cosa sono i numeri naturali
- Cos'è l'addizione
- L’elemento neutro dell’addizione
- Le proprietà dell'addizione
- Cos'è la sottrazione: la sua proprietà
- Proprietà della sottrazione
- Gioca con i numeri
- Interrogazione su addizione e sottrazione
- Sfida: addizione e sottrazione dei numeri naturali
- Gioca con le proprietà di addizione e sottrazione
Cosa sono i numeri naturali
I numeri naturali sono i più intuitivi, quelli che impari da bambino. È questo il motivo per cui è difficile darne una definizione rigorosa.
L’insieme dei numeri naturali £$ \mathbb{N} $£ è l’insieme di tutti i numeri maggiori o uguali a zero: £$\mathbb{N}= \{ 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; …\}$£ Nell’insieme dei numeri naturali, quindi, ci sono tutti i numeri interi e positivi più lo zero, nessun numero negativo e nessuna frazione.
I numeri naturali, così come i punti della semiretta, sono infiniti, puoi partire da zero e andare avanti a elencarli uno ad uno senza mai fermarti!
Attenzione! Alle volte potrai trovare lo [iol_placeholder type="formula" engine="katex" display="inline"/] tra i numeri naturali, alle volte invece viene escluso. Ogni volta che parli di numeri naturali, ricordati di specificare se comprendi lo [iol_placeholder type="formula" engine="katex" display="inline"/] oppure no. Così non ci saranno dubbi!
Cos’è l’addizione
Quanto fa £$2+5$£? E £$374+233$£? Sono tutti calcoli che sai fare ma ti ricordi qual è la definizione di addizione? Hai mai notato che la somma di due numeri naturali è un numero naturale?
La somma di due numeri naturali è il numero ottenuto contando di seguito al primo tutte le unità del secondo. Quindi, per esempio, per calcolare £$5+3$£, parto da £$5$£ e conto altre £$3$£ unità: £$6$£, £$7$£, £$8$£, il risultato è £$8$£!
L’operazione per trovare la somma si chiama addizione ed i numeri da sommare si chiamano addendi.
La somma di due numeri naturali è sempre un numero naturale, quindi la somma è un’operazione interna nell’insieme dei numeri naturali £$ \mathbb{N}$£.
L’elemento neutro dell’addizione

Possiamo sempre calcolare l’addizione tra due o più numeri? Certo! Basta sommare le quantità, cioè gli addendi, e trovare la quantità totale, cioè la somma.
Cosa succede invece se aggiungiamo 0 ad una quantità? Non cambia nulla. Infatti lo 0 è l’elemento neutro per l’addizione: significa che, se aggiungo 0 ad un numero, il totale è uguale a quello stesso numero. Lo 0 è un numero neutrale, non conta nessuna quantità!
Esempio: 14 + 0 = 14, ma anche 0 + 14 = 14.
Le proprietà dell’addizione
Le proprietà dell’addizione sono tre:
- la proprietà commutativa: se scambiamo l’ordine degli addendi, il totale non cambia. Utilizziamo questa proprietà come prova per l’addizione: 23 + 65 = 88 ma anche 65 + 23 = 88. È utile come ulteriore controllo della correttezza dell’operazione;
- la proprietà associativa: sostituendo a due o più addendi la loro somma, il risultato non cambia. Questa proprietà è utile per velocizzare i calcoli a mente: 5 + 3 + 7 = 5 + 10 = 15 è uguale a 5 + 3 + 7 = 8 + 7 = 15, solo che nel primo caso abbiamo sommato prima gli amici del 10 per velocizzare i conti.
- la proprietà dissociativa: la somma di due o più addendi non cambia se a uno di questi sostituiamo più numeri la cui somma sia uguale all’addendo sostituito. Per esempio 32 + 28 diventa 30 + 2 + 28 rendendo più semplice l’addizione: 2 e 8 sono numeri amici!
Le proprietà dell’addizione servono per fare i calcoli più velocemente. Guarda gli esempi e allenati con gli esercizi!
Cos’è la sottrazione: la sua proprietà
Se a £$7$£ togliamo £$5$£ cosa abbiamo? E se a £$5$£ togliamo £$7$£? Il risultato è uguale?
La differenza di due numeri naturali, se esiste, è il numero che aggiunto al secondo dà come somma il primo. L’ operazione per ottenere la differenza è la sottrazione. Dalla definizione possiamo anche dire che la sottrazione è anche l’operazione inversa dell’addizione!
Quindi, £$57-25=32$£ perché se aggiungi £$32$£ a £$25$£ ottieni £$57$£. Puoi anche pensare di avere £$57$£ oggetti e toglierne £$25$£, quanti ne rimangono? £$32$£!
Il primo numero si chiama minuendo, il secondo sottraendo.
Non è sempre possibile calcolare la sottrazione tra due numeri: la sottrazione è possibile solo se il minuendo è maggiore o uguale al sottraendo.
Esempio: possiamo svolgere 18 – 12 perché 18 > 12, ma non possiamo fare la sottrazione 16 – 32 perché il sottraendo è maggiore del minuendo, infatti 16
La sottrazione è l’operazione inversa dell’addizione: se aggiungiamo il resto al sottraendo, il risultato che otteniamo è il minuendo. Se non è così, significa che abbiamo sbagliato qualcosa! Possiamo utilizzare l’addizione come prova della sottrazione per controllare di aver fatto tutto giusto.
Proprietà della sottrazione
La sottrazione ha la sola proprietà invariantiva: la differenza di due numeri non cambia, aggiungendo o togliendo uno stesso numero sia al minuendo sia al sottraendo.
- Esempio: 4 – 2 = 2, ma anche (4 + 3) – (2 + 3) = 7 – 5 = 2
- Esempio: 16 – 12 = 4, ma anche (16 – 2) – (12 – 2) = 14 – 10 = 4
Utilizziamo questa proprietà per rendere più semplici i calcoli, soprattutto quando entrano in gioco i numeri più grandi.
Cosa succede se sottraiamo 0 ad un numero? Non cambia nulla: il resto (o differenza) è uguale al numero stesso.
Viceversa, non possiamo sottrarre alcun numero dallo 0 perché è minore di qualsiasi altro numero: quindi lo 0 non è l’elemento neutro della sottrazione.
Esempio: 23 – 0 = 23, ma 0 – 23 = ? Non sappiamo calcolarlo!
Sottraendo ad un numero lo stesso numero, otteniamo come risultato 0.
Esempio: 16 – 16 = 0
Gioca con i numeri
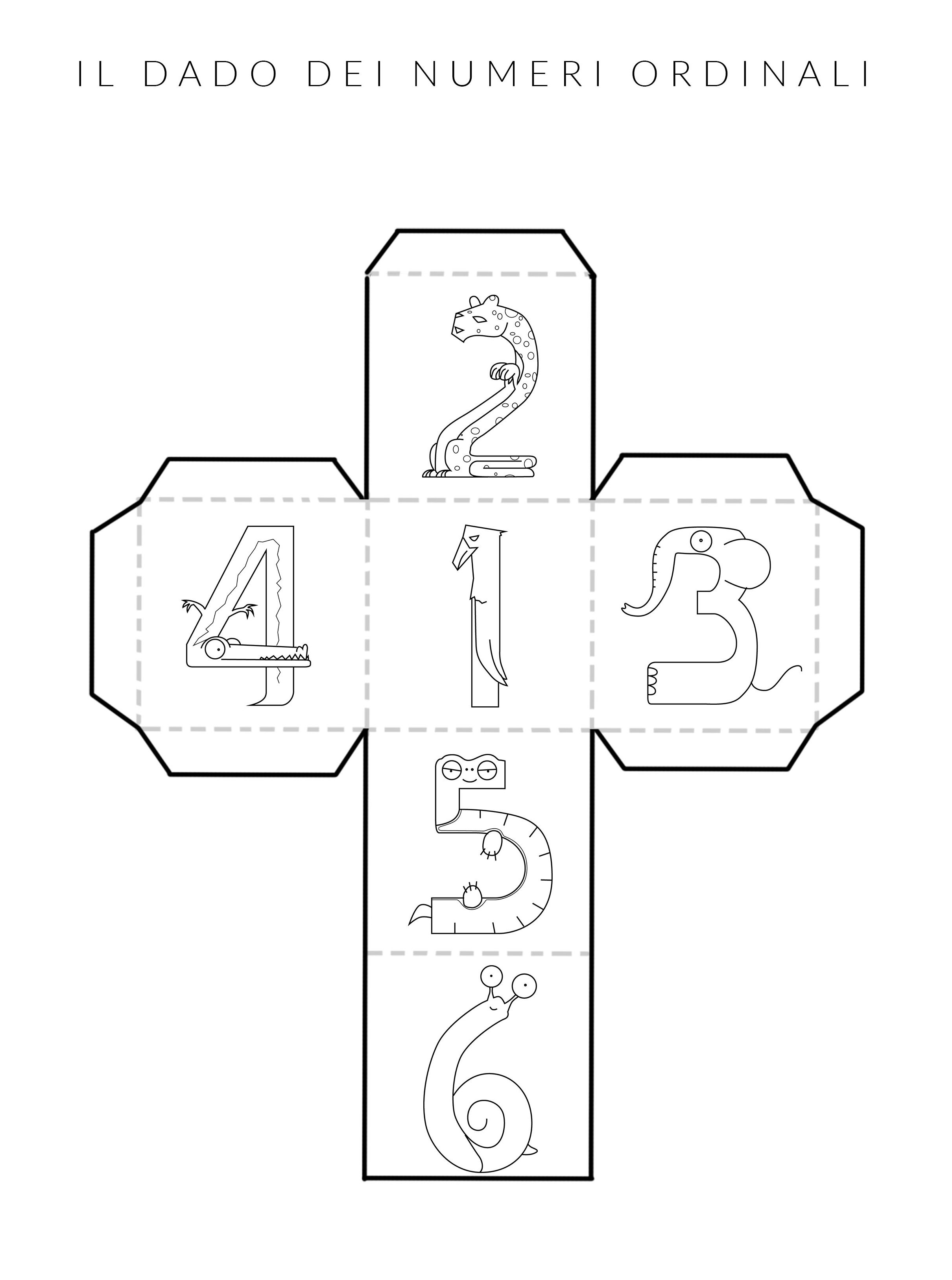
Giochiamo con il dado dei numeri ordinali!
Ogni bambino colora il proprio dado, lo ritaglia e lo costruisce.
Scarica tutto il necessario:
A turno poi i bambini lanciano il dado, leggono il numero che esce (da primo a sesto) e si sfidano a chi taglia per primo il traguardo. Visto che si parla di numeri ordinali, a differenza di quanto avviene di solito, vince chi realizza il numero più basso. Per aiutarti su ogni faccia è disegnato un animale: osserva le immagini e vedrai che il “più veloce" tra gli animali rappresentati è quello che arriva per primo, mentre la più lenta non poteva che essere la povera lumachina. 😉
Tre lanci per il 100
I numeri sono infiniti, così come le addizioni possibili. Ma grazie agli esercizi fatti fino ad ora non avrai problemi a superare anche questa prova! L’ultimo passo sono le addizioni con i numeri più grandi.
Perché non fare un bel gioco con i dadi?
“Tre lanci per il 100": bastano due dadi, magari di due colori diversi (rosso per le decine e blu per le unità). I bambini lanciano i dadi 3 volte, segnano su un foglio il numero ottenuto e sommano. Vince chi arriva più vicino a 100!
Per esempio:
- dal primo lancio il dado rosso totalizza 3 e quello blu 2: scriviamo il numero 32;
- dal secondo lancio otteniamo 1 dal dado rosso e 5 dal dado blu: scriviamo il numero 15;
- dal terzo lancio otteniamo 4 dal dado rosso e 4 dal dado blu: scriviamo il numero 44.
Ora dobbiamo sommare 32 + 15 + 44. Otteniamo 91: un ottimo punteggio! Ci sarà qualcuno che ha ottenuto di più?
Attenti a quei due
Per imparare a velocizzare i conti ecco un altro gioco con i dadi: “Attenti a quei due!". Occorrono 5 dadi che verranno lanciati a turno dai partecipanti. Ogni volta che, nel lancio, escono un 2 o un 5, il totale raggiunto non fa punteggio e si eliminano i dadi che hanno totalizzato 2 o 5, i due numeri da evitare.
Per esempio:
- dal lancio dei 5 dadi escono: 1 – 2 – 6 – 5 – 3. Allora niente punti, eliminiamo due dadi (quello che ha totalizzato 5 e quello che ha totalizzato 2);
- secondo lancio, questa volta solo 3 dadi: escono 3 – 6 – 1. Non c’è traccia di 2 o di 5, possiamo calcolare i punti: 3 + 6 + 1 = 10;
- terzo lancio: usiamo sempre 3 dadi finché non otteniamo un 2 o un 5. Dal terzo lancio otteniamo 4 – 5 – 1. Niente punti, eliminiamo un dado;
- quarto lancio, con due dadi: escono 6 e 2. Di nuovo niente punti, eliminiamo un dado;
- quinto lancio, con un solo dado: esce 4. Possiamo aggiungerlo al nostro punteggio;
- sesto lancio, sempre con un solo dado: esce 2, niente punti.
In totale abbiamo ottenuto 10 + 4 = 14 punti. Non ci saranno conti difficili da fare, ma possiamo proporre questo gioco per migliorare la velocità dei bambini nel riconoscere i numeri e fare rapide somme.
Interrogazione su addizione e sottrazione
Ti senti pronto per l’interrogazione? Qui trovi alcuni esercizi e domande che il prof ti può chiedere. Prova a rispondere! Se hai dei dubbi, puoi sempre riguardare i video per ripassare e prepararti al meglio!
Sfida: addizione e sottrazione dei numeri naturali
Una sfida sui numeri naturali:
Ecco la soluzione:
La sfida dei numeri naturali! Cosa c’entra la matematica con la preparazione della valigia? Quante magliette devi mettere? Prova a risolvere la sfida della lezione. Se hai dubbi, guarda i video spiegati con tanti esempi sulle operazioni e proprietà dell’addizione e sottrazione nei numeri naturali, che ti aiuteranno a trovare la soluzione alla sfida!
Gioca con le proprietà di addizione e sottrazione
Più 1, meno 1, più 10, meno 10
Le proprietà dell’addizione
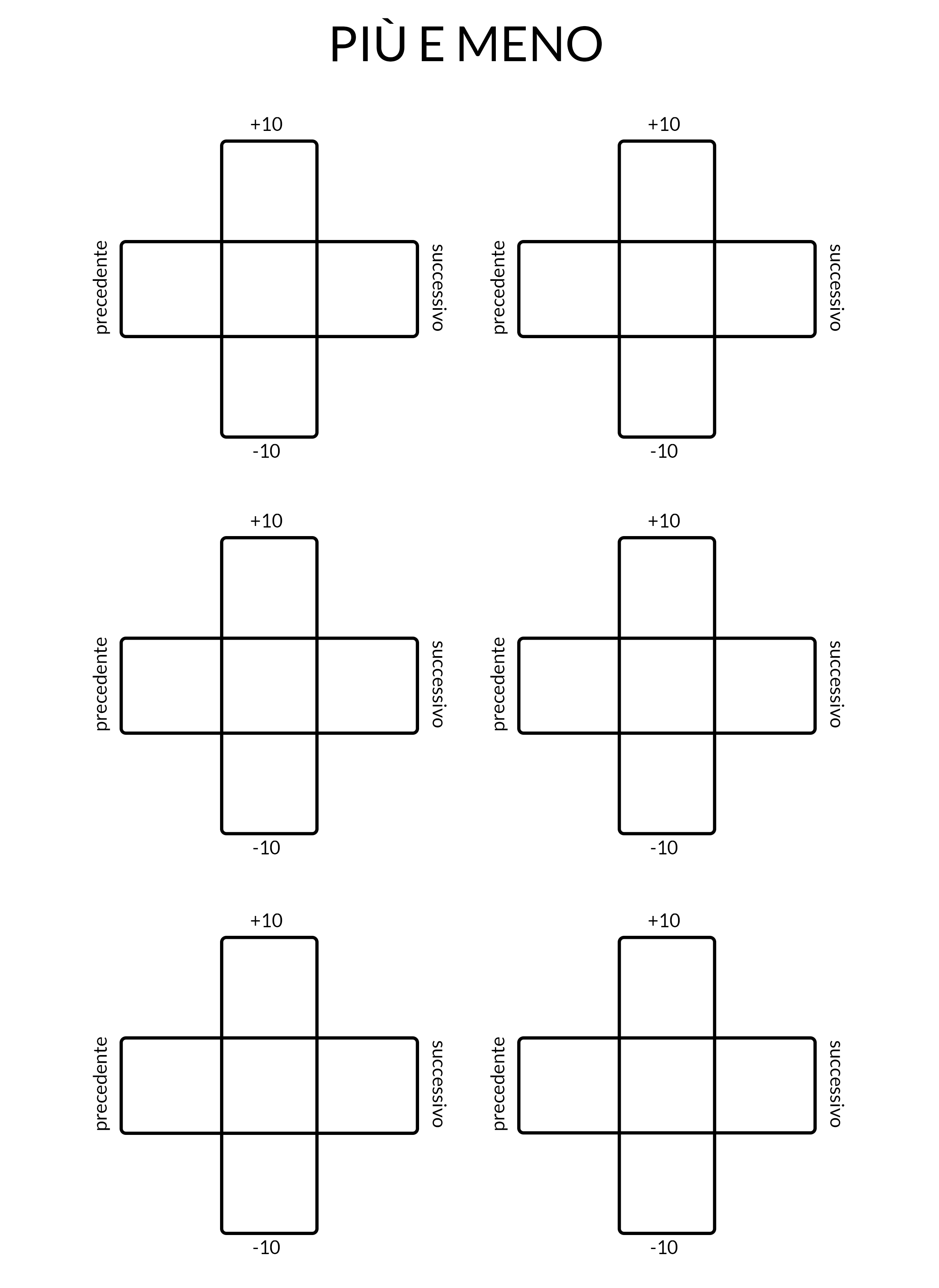
I ragazzi non digeriscono proprio addizioni e sottrazioni? Iniziamo a fare calcoli semplici: numero precedente e successivo, o semplicemente +10 e –10. Estraete un numero che i vostri alunni dovranno inserire al centro di ciascuna croce; quindi dovranno completare lo schema trovando il numero precedente e successivo, aggiungendo e sottraendo 10.
Scarica qui la scheda:
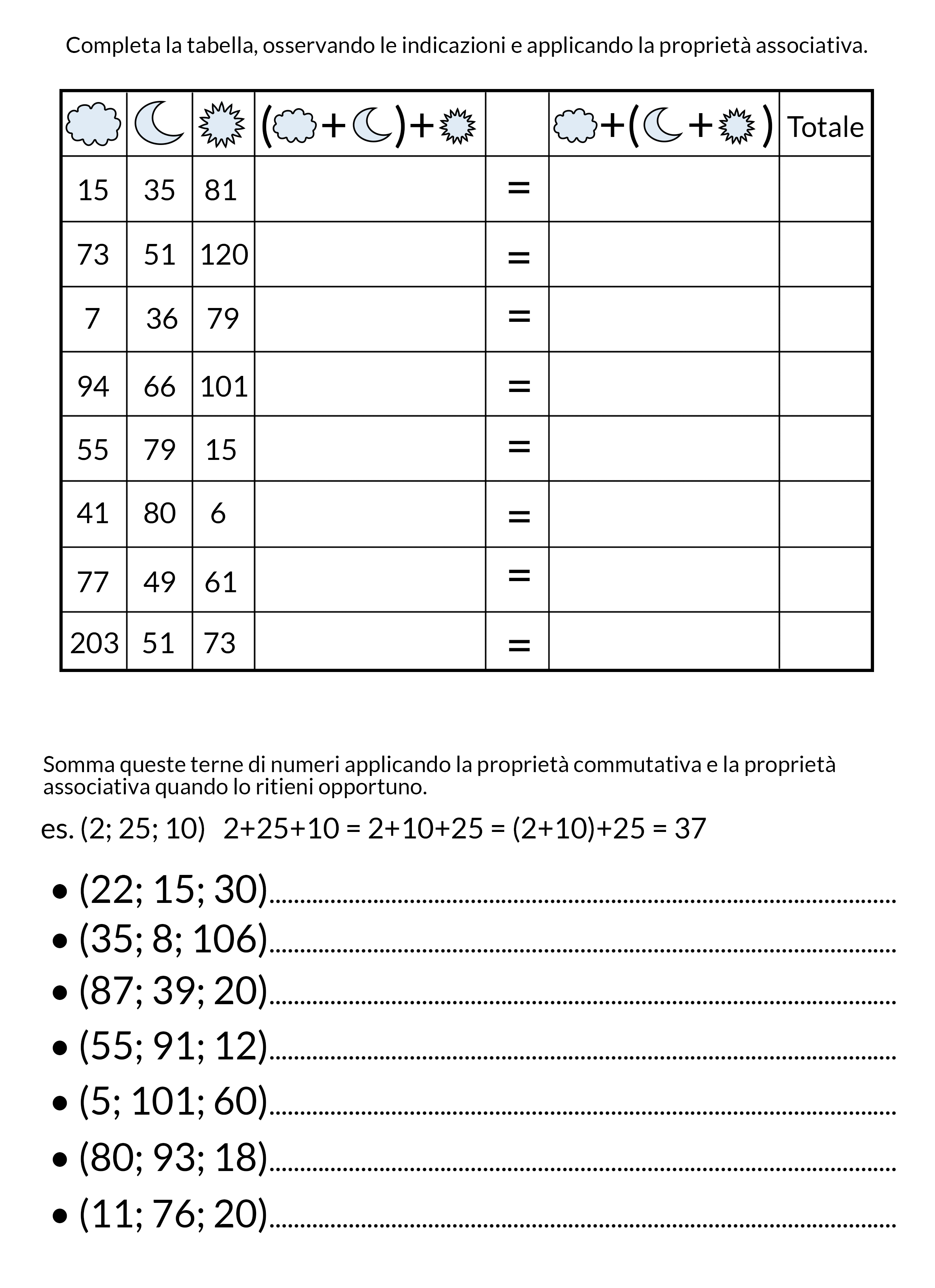
Aggiungiamo poi una scheda con esercizi utili per capire come utilizzare le proprietà di queste due operazioni.
Scarica qui la scheda:
Vi proponiamo un gioco per trascorrere il tempo, allenando la mente a velocizzare i calcoli: bastano due dadi e un foglio per aiutarsi con i conti. Non c’è un limite di partecipanti! Basta tirare i dadi: in ciascuna coppia di dadi, uno indica la cifra delle decine e uno indica quella delle unità. Ogni giocatore, a turno, lancia i dadi 5 volte e somma tutti i numeri ottenuti in successione. Vince chi arriva più vicino a 200 come risultato finale. Potete fare lo stesso gioco al contrario, cioè partendo da 200 e sottraendo in successione tutti i numeri ottenuti dal lancio dei dadi: questa volta vince chi arriva più vicino a 0. Capiterà di ritrovarsi davanti ad una “sottrazione impossibile", in cui il minuendo è minore del sottraendo: scegliete voi il premio per chi se ne accorge. 😉
Infine un gioco di carte per allenare la velocità di conto: la guerra delle addizioni. I ragazzi si sfidano a coppie, ognuno con il proprio mazzo di carte (senza figure né jolly). Dopo aver mescolato le carte, i due giocatori girano la prima carta del mazzo, quindi osservano quella dell’avversario e calcolano la somma. Il primo che dice il risultato corretto, conquista entrambe le carte. Vince chi riesce a conquistare più carte… a colpi di addizioni!
