La sottrazione: come si fa e quali sono le sue proprietà
La sottrazione è una delle quattro operazioni matematiche fondamentali che incontriamo sin dai primi anni di scuola. Pensiamola in questo modo: abbiamo un gruppo di biscotti e vogliamo vedere quanti ne rimangono se alcuni vengono mangiati.
La sottrazione ci aiuta a rispondere a questa domanda e a capire quanti biscotti abbiamo già mangiato.. o quanti ne potremo mangiare dopo! Quando sottraiamo, prendiamo un numero, chiamato minuendo, e togliamo da esso un altro numero, chiamato sottraendo. Il risultato di questa operazione è chiamato differenza.
Così, ogni volta che vogliamo scoprire quanto rimane dopo aver tolto una certa quantità, facciamo ricorso alla sottrazione: scopriamo come farla!
- I nomi dei termini della sottrazione
- La differenza: quando non è possibile calcolarla
- Proprietà invariantiva della sottrazione
- Addizione e sottrazione... al supermercato!
- Come sottrarre 17 - 9
- Come sottrarre 16-9
- Sottrazioni fino al 100 e al 1000
- Mappa mentale della sottrazione
- Schede di esercizi con le sottrazioni
- Esercizi sulle sottrazioni in colonna
- Esercizi sulla proprietà invariantiva della sottrazione
I nomi dei termini della sottrazione
La sottrazione è l’operazione che svolgiamo per togliere una quantità ad un’altra, cioè sottrarre un numero ad un altro.
Il segno aritmetico che indica la sottrazione è £$ – $£ che leggiamo meno.
I due numeri che sottraiamo uno all’altro sono il minuendo e il sottraendo e sono separati dal segno £$ – $£. Possiamo scrivere, ad esempio, la sottrazione £$ 8 – 3 $£, dove £$ 8 $£ è il minuendo e £$ 3 $£ è il sottraendo.
Quando parliamo di sottrazioni, le indichiamo anche come differenze: questo perché il risultato di questa operazione si chiama proprio differenza.
$$ 8 – 3 = 5 $$
£$ 8 $£ è il minuendo, £$ 3 $£ è il sottraendo, £$ 5 $£ è la differenza
La differenza: quando non è possibile calcolarla
Diversamente da quanto accade per l’addizione, non è sempre possibile calcolare una sottrazione.
La somma di due numeri naturale è sempre un numero naturale: calcolando un’addizione ricadiamo sempre nell’insieme £$ \mathbb{N} $£, quindi ritroviamo sempre un numero che conosciamo.
Possiamo calcolare una sottrazione solamente se il minuendo è maggiore del sottraendo: solo in questo caso ricadiamo all’interno dell’insieme dei numeri naturali £$ \mathbb{N} $£. Nel caso in cui il sottraendo fosse maggiore del minuendo, non siamo ancora capaci di trovare il risultato: è un numero sotto alla [iol_placeholder type="formula" engine="katex" display="inline"/], cioè un numero negativo, che appartiene all’insieme dei numeri relativi.
Esempio:
- possiamo calcolare la sottrazione £$ 15 – 2 $£ perché £$ 15 > 2 $£, quindi il risultato è ancora in £$ \mathbb{N} $£. Infatti £$ 15 – 2 = 13 \in \mathbb{N} $£;
- non possiamo calcolare £$ 8 – 10 $£ perché [iol_placeholder type="formula" engine="katex" display="inline"] 8
Per questo la sottrazione non ha un elemento neutro. Infatti se sottraiamo £$ 0 $£ a un numero, otteniamo il numero stesso, ma non vale il viceversa.
$$ 67 – 0 = 67 \text{ ma } 0 – 67 = \ ? $$
Proprietà invariantiva della sottrazione
La sottrazione è l’operazione inversa dell’addizione.
L’unica proprietà della sottrazione è la proprietà invariantiva: se aggiungiamo o togliamo una stessa quantità ai numeri di cui stiamo facendo la differenza, il risultato non cambia.
Infatti l’aggettivo “invariantiva" deriva da “invariante" che significa che non cambia, resta invariato.
Esempio: proviamo a risolvere £$ 23 – 15 = 8 $£.
Se proprio vogliamo complicarci le cose, possiamo risolverlo così: £$ (23 + 5) – (15 + 5) = 28 – 20 = 8 $£.
Altrimenti, per semplificarle un po’ facciamo così: £$ (23 – 3) – (15 – 3) = 20 – 12 = 8 $£.
Per la sottrazione non vale la proprietà commutativa e nemmeno la proprietà associativa.
Trovi la tabella con tutte le formule qui.
Addizione e sottrazione… al supermercato!
Calcoliamo addizioni e sottrazioni ogni giorno, anche quando andiamo a fare la spesa al supermercato.
Possiamo fare queste operazioni anche con numeri con la virgola, cioè numeri non interi, che non appartengono all’insieme dei numeri naturali £$ \mathbb{N} $£.
È il caso dei prezzi che leggiamo al supermercato: sono quasi tutti numeri con la virgola, formati da una parte intera (il numero prima della virgola) e una parte decimale (il numero dopo la virgola).
Guarda il video e prova a fare i conti applicando anche le proprietà di addizioni e sottrazioni che hai imparato!
Come sottrarre 17 – 9
Consideriamo un’altra operazione: 17 – 9.
Prendo l’asticina neutra numero 1 e la posiziono in modo da coprire il 18 rosso sulla tavola. Poi prendo l’asta blu numero 9 e la posiziono di fianco a quella neutra, quindi leggo il risultato. Il risultato è 8.
Come sottrarre 16-9
Facciamo un ultimo esempio: 16 – 9.
Prendo l’asticina neutra numero due e la posiziono sulla tavola in modo da coprire 18 e 17. Posiziono l’asticina blu numero 9 a fianco a quella neutra e leggo il risultato. Il risultato è 7.
Sottrazioni fino al 100 e al 1000
I numeri si fanno più grandi, ma la tecnica è sempre la stessa.
Quando impariamo a fare sottrazioni fino a 100, ci esercitiamo a sottrarre numeri più piccoli, come ad esempio 75 – 30, che ci dà come risultato 45. Questo tipo di sottrazioni è utile per risolvere problemi quotidiani semplici, come calcolare quanti soldi rimangono dopo un acquisto o determinare quante caramelle sono state mangiate da un sacchetto.
Progredendo, impariamo a fare sottrazioni fino a 1000, che ci permettono di lavorare con numeri più grandi e di affrontare problemi più complessi. Ad esempio, 850 – 420 ci dà 430. Queste sottrazioni sono importanti per situazioni come gestire budget più grandi, calcolare differenze di quantità su scala maggiore o risolvere problemi matematici dettagliati.
Mappa mentale della sottrazione
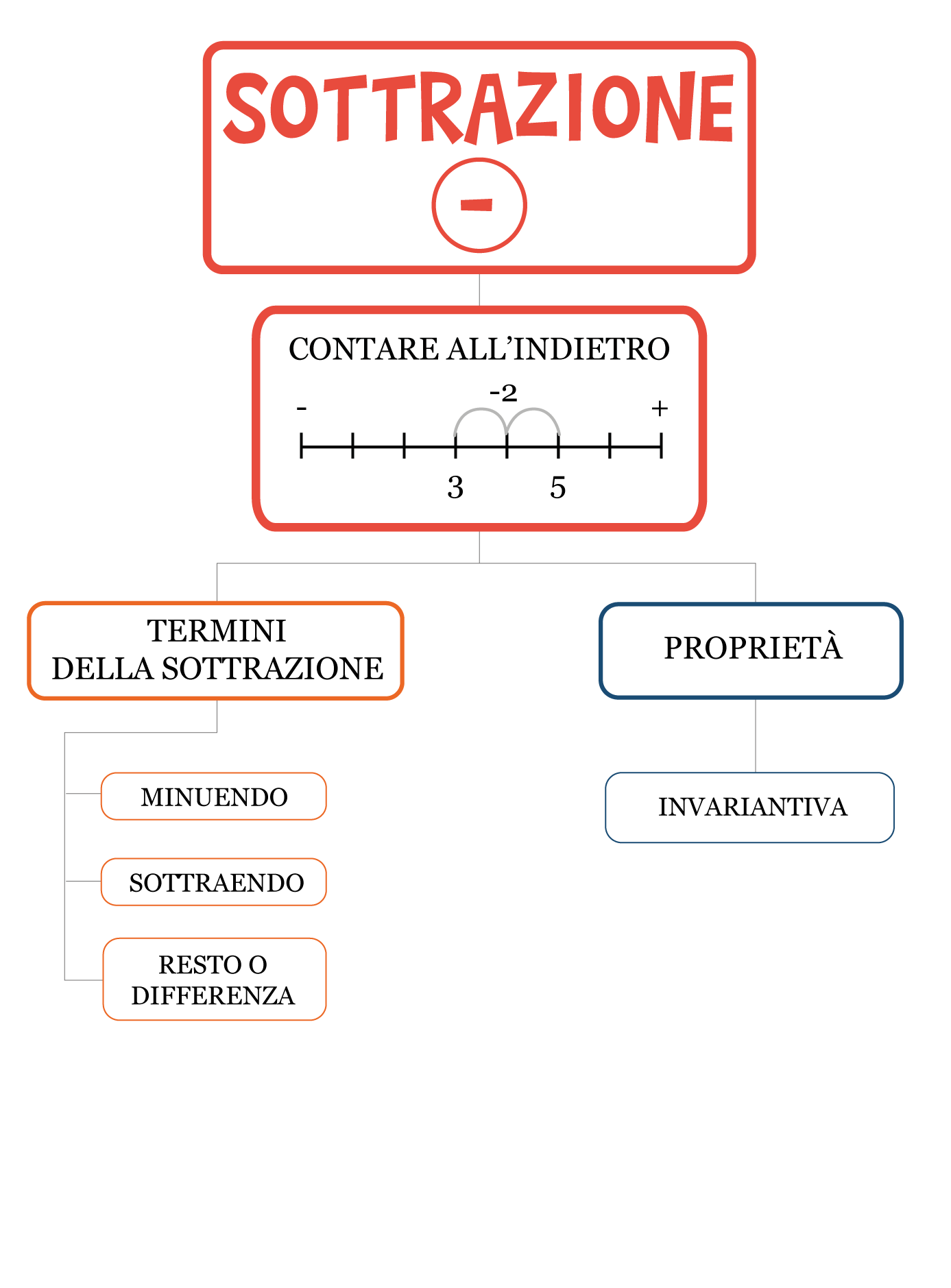
Ripassa tutti gli elementi della sottrazione con l’aiuto della mappa mentale.
Scarica la mappa e stampala per portarla sempre con te:
Schede di esercizi con le sottrazioni
A seguire, delle schede in livelli di difficoltà crescenti per esercitarti con le sottrazioni con i numeri a una o due cifre: sottrazioni fino al 9, fino al 20 e con il riporto.
- Sottrazioni fino al 9
Scarica la scheda qui:
- Sottrazioni fino al 20
Scarica la scheda qui:
- Sottrazioni in colonna
Scarica la scheda qui:
Schede di esercizi per imparare ad applicare le proprietà della sottrazione.
Tanti esercizi pronti da stampare per essere utilizzati in classe o come compito a casa.
Esercizi sulle sottrazioni in colonna

Qualche utile esercizio di calcolo per imparare a risolvere le sottrazioni in colonna.
Scarica la scheda qui:
Esercizi sulla proprietà invariantiva della sottrazione
Infine, due schede pronte da stampare con tantissimi esercizi sulla proprietà invariantiva della sottrazione.
Scarica qui i due pdf:
Continua a sottrarre senza paura e diventa il migliore! Buon allenamento!
