I polinomi numerici: cosa sono
Cosa sono i polinomi numerici? Sono particolari scomposizioni di numeri molto grandi che riusciamo a fare grazie alle potenze di 10. Per esempio 10£$^2$£ è come scrivere 100, un 1 seguito da due zeri.
In questo contesto, un numero viene espresso come la somma di termini, ciascuno dei quali è un prodotto di un coefficiente e una potenza di 10. Ad esempio, il numero 3456 può essere rappresentato come £$3×10 ^3 +4×10 ^2 +5×10 ^1 +6×10 ^0 $£. In questa scomposizione, ogni cifra del numero è moltiplicata per una potenza di 10 corrispondente alla sua posizione nel numero, partendo da destra con £$10^0$£ (che vale sempre 1) e aumentando l’esponente di 1 per ogni posizione spostandosi verso sinistra.
Vediamo insieme come fare.
- Le potenze di 10
- Sistema di numerazione decimale, in base 10
- Come usare le potenze di 10
- Scheda attività numeri molto grandi
- Schede esercizi per imparare i polinomi numerici
Le potenze di 10
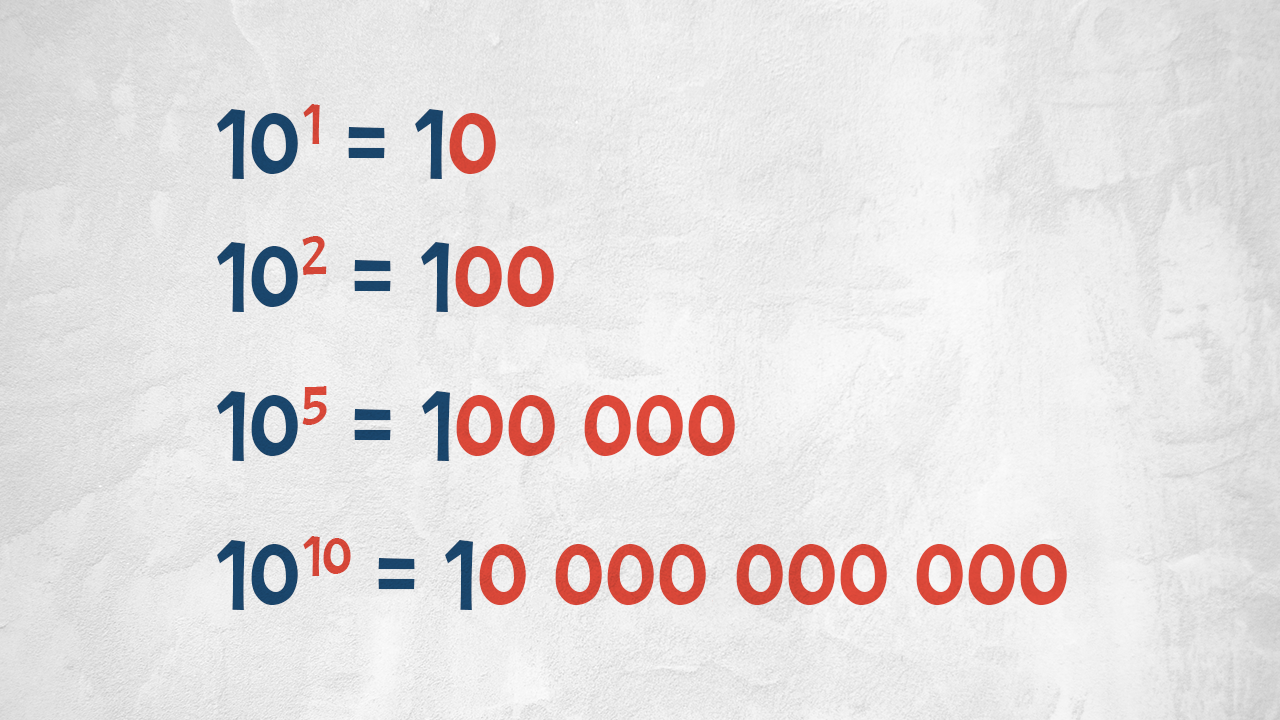
Ricordi cosa sono le potenze? Una potenza è un modo più veloce per scrivere una moltiplicazione. Possono essere utili anche per scrivere in modo più compatto un numero molto grande: possiamo utilizzare le potenze di 10.
Le potenze di 10 sono le più semplici: il numero degli zeri coincide con quanto indicato dall’esponente.
Esempio:
- 10 = 10£$^1$£ perché c’è un solo zero dopo l’1;
- 1000 = 10£$^3$£ perché l’1 è seguito da tre zeri;
- 100 000 000 = 10£$^8$£ perché ci sono otto zeri dopo l’1.
Sistema di numerazione decimale, in base 10
Il nostro sistema di numerazione è un sistema decimale, cioè è un sistema di numerazione posizionale in base 10.
Il numero 10 ritorna spesso in gioco quando parliamo di numeri: utilizziamo 10 cifre (da 0 a 9); ogni cifra ha un valore diverso a seconda della posizione in cui si trova; il valore di ciascuna cifra differisce di una potenza di 10 (1 centinaio è uguale a 10 decine, uguale a 100 unità e così via)…
Possiamo utilizzare il 10 per scrivere i numeri molto grandi in modo compatto: scopriamo un altro modo per scrivere i numeri in base 10.
Come usare le potenze di 10
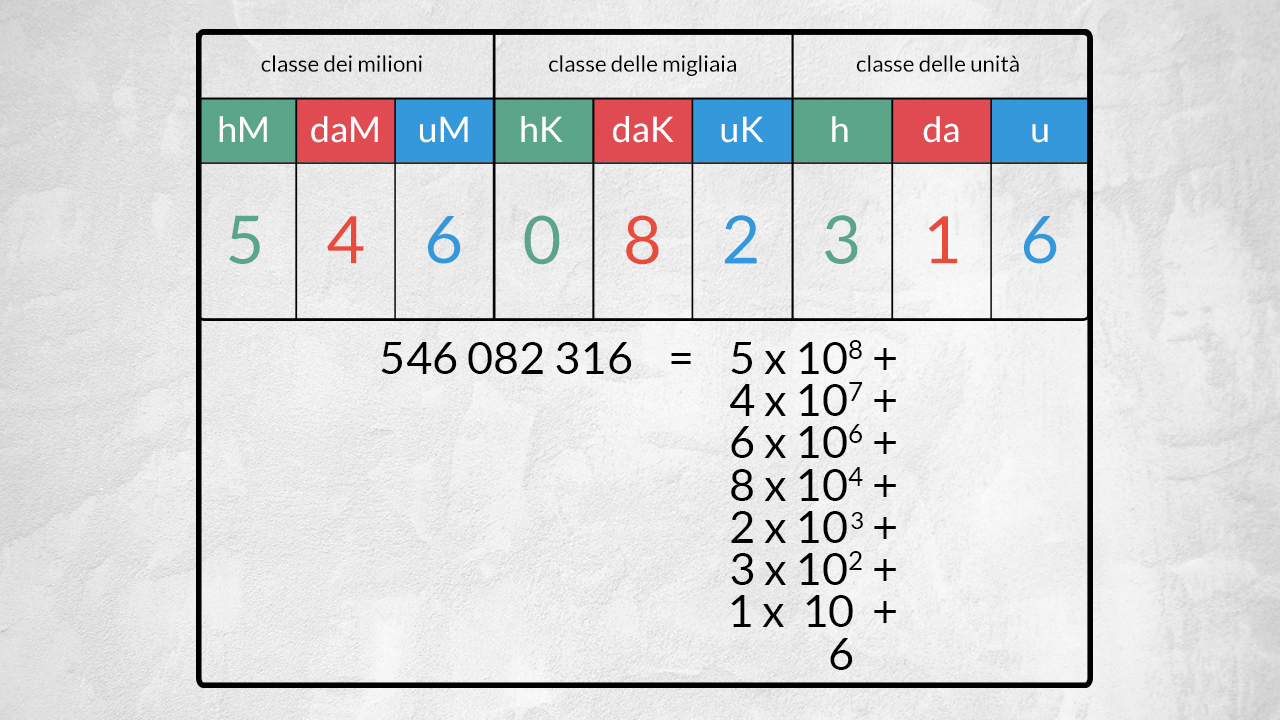
Come possiamo utilizzare le potenze di 10 per scrivere i numeri molto grandi? Proviamo a scomporre un numero come somma di prodotti:
| 546 082 316 = | (5 x 100 000 000) + |
| (4 x 10 000 000) + | |
| (6 x 1 000 000) + | |
| (8 x 10 000) + | |
| (2 x 1000) + | |
| (3 x100) + | |
| (1 x 10) + | |
| 6 |
Grazie alle potenze di 10, possiamo scrivere questa scomposizione più brevemente:
546 082 316 = 5 x 10£$^8$£ + 4 x 10£$^7$£ + 6 x 10£$^6$£ + 8 x 10£$^4$£ + 2 x 10£$^3$£ + 3 x 10£$^2$£ + 1 x 10 + 6
Questo è un polinomio numerico: è la somma dei prodotti di un numero per una potenza di 10. L’esponente corrisponde alla posizione che occupa ciascuna cifra all’interno del numero.
Possiamo scrivere tutti i numeri come polinomi numerici. Abbiamo scoperto un altro modo per scrivere la scomposizione di un numero, anche un numero molto grande.
Scheda attività numeri molto grandi

Spesso i bambini avranno a che fare con i numeri molto grandi, in scienze, in geografia…
Scomponendo questi grandi numeri con i polinomi numerici, possono avere più chiaro l’ordine di ciascun numero, quindi capire quali sono i più grandi e quali i più piccoli. Leggendo i numeri nel modo corretto, possono farsi un’idea più precisa anche delle dimensioni di una regione o di una città.
Proponete loro altre attività di questo tipo per prendere confidenza con i grandi numeri, che non siano numeri casuali, ma magari numeri che li portino a incuriosirsi e indagare su alcuni aspetti delle altre discipline.
Insistete sul fatto che la posizione di ciascuna cifra ha un valore diverso, che possiamo rappresentare attraverso una potenza di 10. Ritorniamo sul concetto del sistema decimale posizionale che abbiamo studiato in terza, con l’aggiunta dei numeri molto grandi.
Scaricate la nostra scheda con qualche esercizio per imparare a leggere e scomporre migliaia, milioni e miliardi attraverso i polinomi numerici:
Schede esercizi per imparare i polinomi numerici
Unità, decine, centinaia di migliaia: tante schede e giochi per imparare a riconoscere e scomporre i numeri di tre o più cifre. Leggi, scarica e stampa tutte schede di esercizi sulle migliaia!
Una rapida verifica per controllare le competenze.
Scarica qui la scheda:
Sistema decimale posizionale
Una scheda per ripassare il valore delle cifre a seconda della loro posizione, con unità, decine e centinaia.
Scarica la scheda qui:
Scrittura migliaia e scomposizione
Esercizi per riconoscere il valore delle cifre di un numero in funzione della posizione.
Scarica le due schede qui:
Confronto di numeri
Qualche esercizio di confronto tra numeri per imparare a inserire il simbolo corretto: [iol_placeholder type="formula" engine="katex" display="inline"] >,
Scarica la scheda qui:
Ordine dei numeri
Esercizi per imparare a ordinare i numeri in modo crescente o decrescente.
Scarica la scheda qui:
Polinomi numerici
Una scheda da stampare per preparare la verifica sui polinomi numerici.
Scarica la scheda qui:
