Il prodotto cartesiano: cos'è e quali sono le sue proprietà

Quando ci avviciniamo al mondo della matematica e, in particolare, alla teoria degli insiemi, una delle operazioni fondamentali che incontriamo è il “prodotto cartesiano“. Questo nome, che può sembrare enigmatico a prima vista, ha le sue radici storiche: è un tributo a René Descartes, il matematico e filosofo francese noto per la sua rivoluzionaria introduzione del sistema di coordinate cartesiane in geometria.

Ma cosa è esattamente il prodotto cartesiano? In termini semplici, è un metodo per combinare due insiemi, generando tutte le possibili coppie ordinate degli elementi di questi insiemi. Prendiamo, ad esempio, un insieme di numeri {1, 2} e un insieme di lettere {a, b}. Il prodotto cartesiano di questi due insiemi ci dà {(1, a), (1, b), (2, a), (2, b)}, rappresentando tutte le combinazioni possibili tra i numeri e le lettere.

In questo articolo, esploreremo in dettaglio la definizione del prodotto cartesiano, di diagramma cartesiano e cos’è e come si compone una tabella a doppia entrata. Pronti? Cominciamo!

• Il prodotto cartesiano: cos'è e quando lo usiamo
• Come rappresentare il prodotto cartesiano
• Proprietà del prodotto cartesiano
• Interrogazione sul prodotto cartesiano
• Sfida sul prodotto cartesiano

Il prodotto cartesiano: cos’è e quando lo usiamo

Abbiamo imparato come fare unione e intersezione tra due insiemi. Ma esiste un’altra operazione. Come per i numeri, possiamo fare anche la moltiplicazione tra insiemi attraverso il prodotto cartesiano.

Indichiamo questa operazione con un simbolo che ricorda molto quello che utilizziamo per la moltiplicazione tra numeri: £$ \times $£.

Prendiamo due insiemi £$ A $£ e £$ B $£.

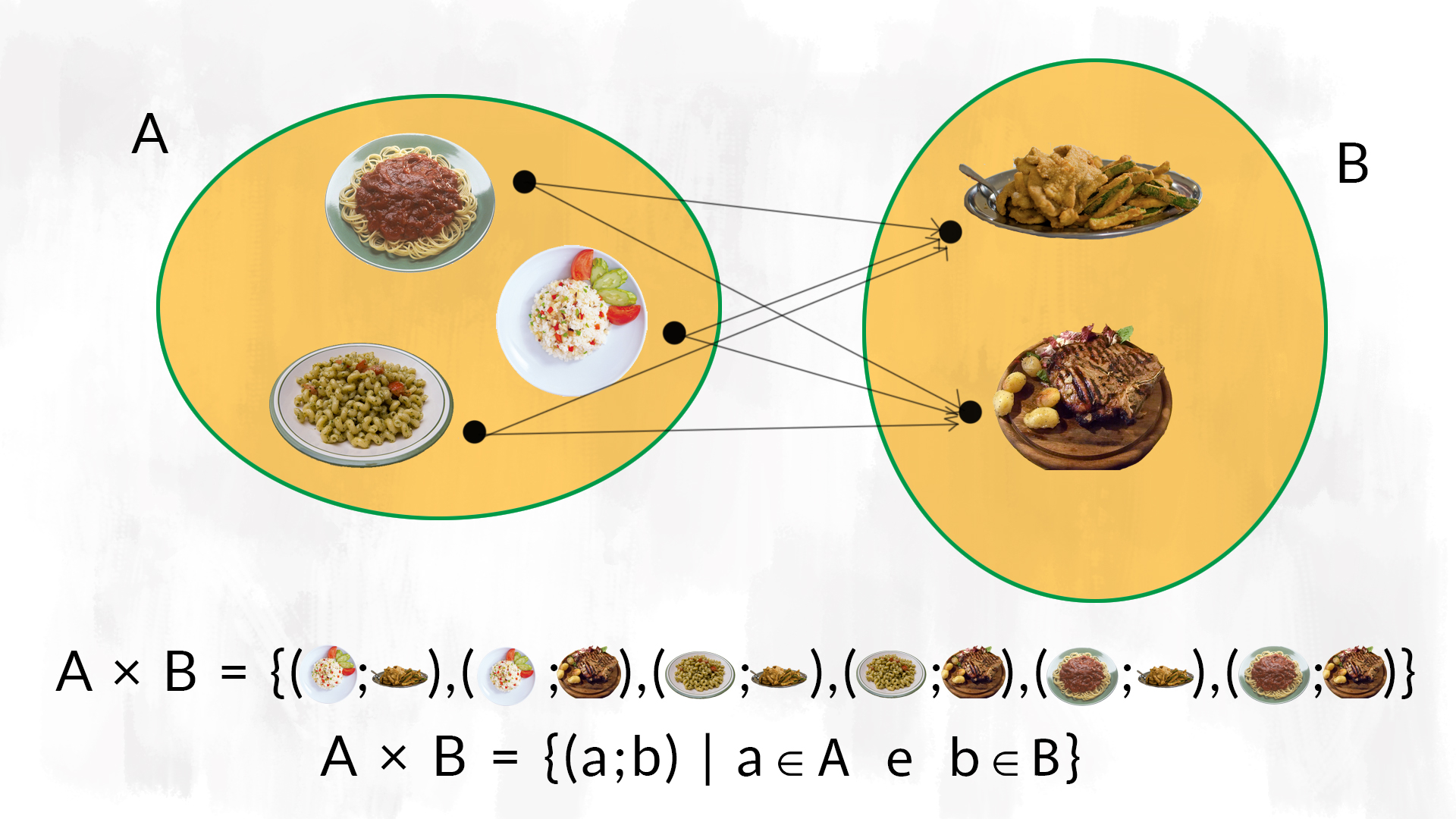
Il prodotto cartesiano è l’insieme di tutte le coppie £$ (a; b) $£ con £$ a \in A $£ e £$ b \in B $£. L’insieme di queste coppie è l’insieme £$ A \times B $£ e contiene un numero di elementi pari al prodotto del numero di elementi di £$ A $£ per il numero di elementi di £$ B$£.

Diciamo che la cardinalità – la cardinalità è il numero di elementi di un insieme – dell’insieme prodotto cartesiano è uguale al prodotto delle cardinalità dei due insiemi di partenza.

Esempio:

£$ A = \{ 1,2,3 \} $£ e £$ B = \{2,3 \} $£. Allora il prodotto cartesiano è l’insieme

$$ A \times B = \{ (1;2), (1; 3), (2;2), (2;3), (3; 2), (3;3) \} $$

Questo insieme contiene 6 elementi, che è proprio uguale al prodotto dei 3 elementi di £$ A $£ per i 2 elementi di £$ B $£.

Gli elementi del prodotto cartesiano sono coppie ordinate. È importante l’ordine degli elementi nella coppia: infatti £$ (2; 3) \ne (3; 2) $£. Dobbiamo inserire entrambe le coppie nell’insieme prodotto, una non esclude l’altra: coppie diverse forniscono informazioni diverse.

Nell’immagine vediamo il prodotto cartesiano tra due insiemi, uno che contiene dei primi piatti e uno che contiene dei secondi piatti. Si capisce bene che il prodotto cartesiano è l’insieme di tutti i possibili menu che possiamo scegliere componendo le diverse pietanze. Ogni volta che esci a pranzo, fai un prodotto cartesiano. Incredibile, vero?

Trovi la tabella con tutte le formule qui.

Come rappresentare il prodotto cartesiano

Esistono diversi modi per rappresentare questa operazione tra insiemi. Corrispondono in parte a quelli che abbiamo già visto per gli insiemi e nell’esempio del primo post:

• rappresentazione con un diagramma a frecce: il prodotto cartesiano è rappresentato dalle frecce che collegano ciascun elemento del primo insieme a ciascun elemento del secondo insieme;
• rappresentazione per elencazione: elenchiamo tutte le coppie che si formano con il prodotto cartesiano;
• rappresentazione per caratteristica: per definizione, l’insieme £$ A \times B $£ è l’insieme delle coppie di elementi tali che il primo appartiene all’insieme £$ A $£ e il secondo appartiene all’insieme £$ B $£, cioè, scritto in linguaggio matematico, $$ A \times B = \{ (a; b) | a \in A, b \in B \} $$

Qual è la novità quindi? Esistono altri modi più intuitivi per rappresentare questa operazione:

• la tabella a doppia entrata: costruiamo una tabella in cui inseriamo gli elementi dei due insiemi e quindi le coppie che si formano con il prodotto cartesiano;
• il diagramma cartesiano: sicuramente il termine cartesiano ti fa tornare in mente il piano cartesiano. Infatti è proprio quello che utilizziamo per questa rappresentazione: posizioniamo sull’asse delle £$ x $£ gli elementi del primo insieme e sull’asse delle £$ y $£ quelli del secondo insieme. Il prodotto cartesiano individua dei punti sul piano cartesiano: possiamo infatti vedere le coppie di elementi come le coordinate dei punti sul piano. Ecco l’importanza dell’ordine degli elementi nelle coppie: il punto £$ (2;3) $£ è diverso dal punto £$ (3; 2) $£.

Osserva nelle immagini i differenti modi per rappresentare il prodotto cartesiano tra gli insiemi £$ A = \{ 1,2,3,4 \} $£ e £$ B = \{5, 6 \} $£.

Diagramma cartesiano

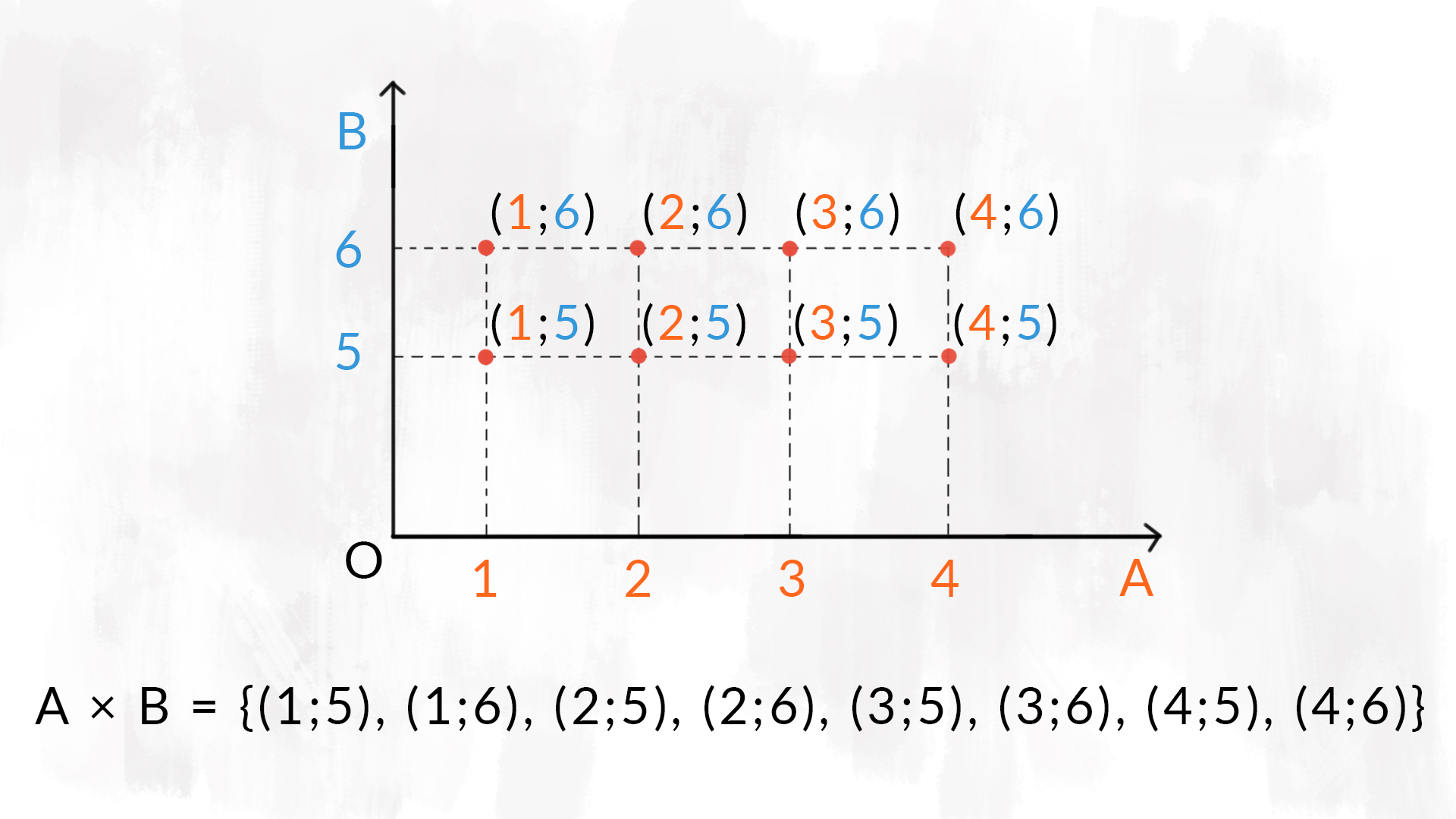
Tabella a doppia entrata

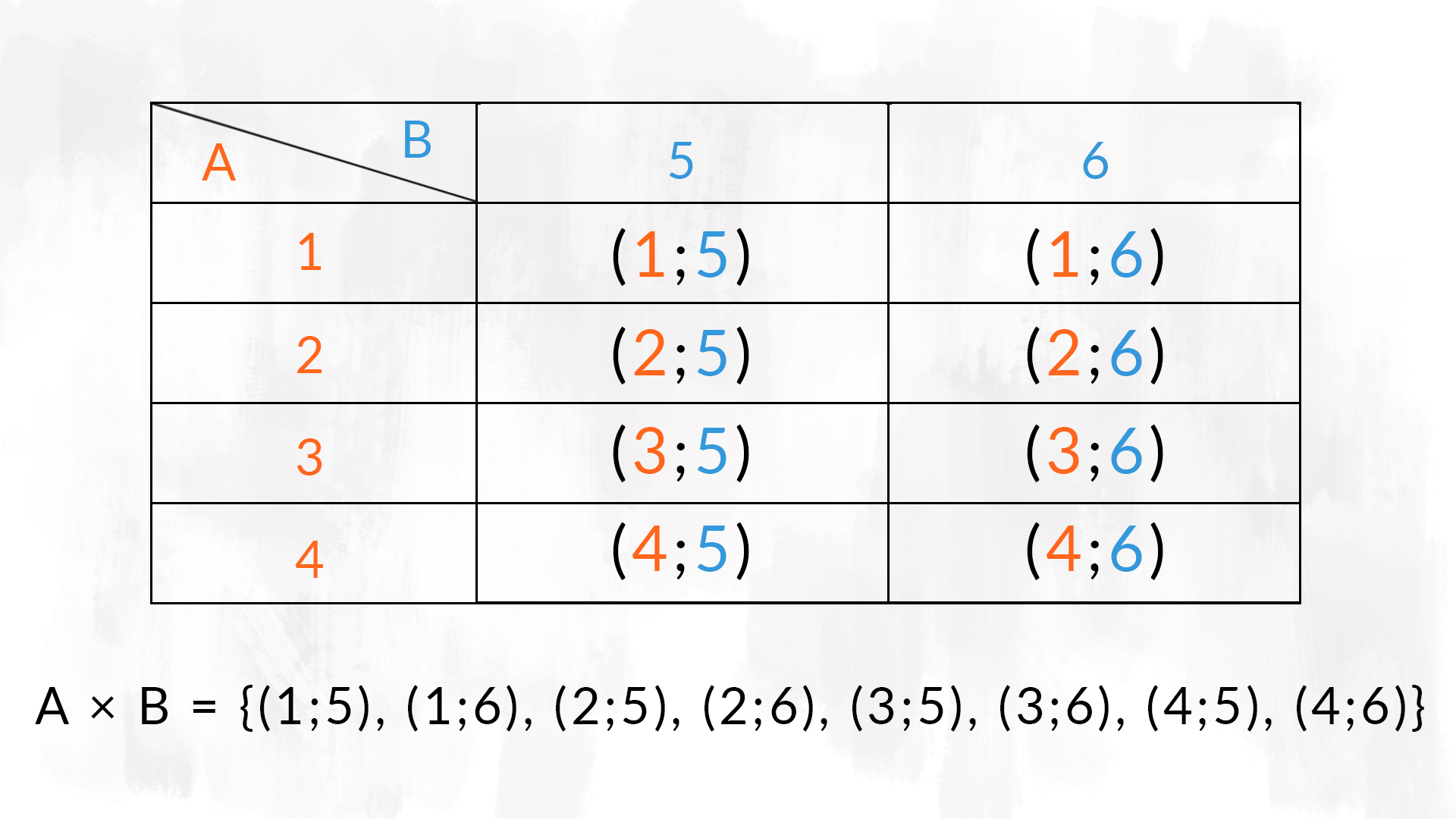
Diagramma cartesiano

Il diagramma cartesiano è una rappresentazione grafica del prodotto cartesiano tra due insiemi, che utilizza due semirette fra loro perpendicolari.

Sulla semiretta orizzontale rappresentiamo gli elementi del primo insieme, su quella verticale gli elementi del secondo insieme.

Da ogni elemento del primo insieme tracciamo una semiretta verticale, da ogni elemento del secondo tracciamo una semiretta orizzontale.

Queste semirette formano una griglia. I nodi della griglia rappresentano le coppie del prodotto cartesiano.

Tabella a doppia entrata

La tabella a doppia entrata è utilizzata per rappresentare il prodotto cartesiano tra due insiemi, £$A \times B$£, in cui:

• nella prima colonna sono riportati gli elementi di £$A$£ e
• nella prima riga gli elementi di £$B$£.

Su ogni altra cella della tabella si riportano le coppie di elementi di £$A \times B$£ rappresentati dall’elemento di £$A$£ della riga in cui si trova la cella e dall’elemento di £$B$£ della colonna in cui si trova la cella.

Proprietà del prodotto cartesiano

Il prodotto tra insiemi è un’operazione simile al prodotto tra numeri. Vediamo alcuni casi particolari.

Cosa succede se dobbiamo trovare il prodotto cartesiano tra un insieme e se stesso? Consideriamo l’insieme £$ A = \{ a, b \} $£ e cerchiamo l‘insieme £$ A \times A $£: funziona esattamente come con i numeri! Stiamo calcolando il quadrato di un insieme. Infatti:

$$ A \times A = A^2 = \{ (a;a), (a;b), (b;a), (b;b) \} $$

Che insieme è il prodotto cartesiano tra un insieme £$ A = \{a,b \} $£ e l’insieme vuoto £$ \varnothing $£? Anche in questo caso funziona come per i numeri. Il risultato di questo prodotto è analogo al risultato del prodotto di un numero per £$ 0 $£, cioè è uguale allo zero degli insiemi.

$$ A \times \varnothing = \varnothing $$

Per il prodotto cartesiano non vale la proprietà commutativa: infatti le coppie che si formano con il prodotto cartesiano, sono coppie ordinate di elementi. Invertendo l’ordine dei due insiemi, abbiamo delle coppie diverse.

$$ A \times B \ne B \times A $$

Valgono poi delle altre proprietà particolari, riconducibili alla proprietà distributiva che abbiamo studiato per i numeri. Le vediamo velocemente:

• £$ A \times (B \cup C) = (A \times B) \cup (A \times C) $£
• analogamente £$ ( A \cup B) \times C = (A \times C) \cup (B \times C) $£
• £$ A \times (B \cap C) = (A \times B) \cap (A \times C) $£
• analogamente £$ ( A \cap B) \times C = (A \times C) \cap (B \times C) $£

Interrogazione sul prodotto cartesiano

Sei in panico per l’interrogazione di domani sul prodotto cartesiano? Non preoccuparti ti aiutiamo noi con questa simulazione di interrogazione!

Sfida sul prodotto cartesiano

Sfida:

Soluzione:

Come rappresentare in modo rapido quali piloti di MotoGP appartengono a quali scuderie? Facile con gli insiemi! Prova a risolvere la sfida e se proprio non riesci guarda la soluzione!