Gli insiemi: diagramma a frecce e relazioni in tabella
Gli insiemi sono un concetto fondamentale in matematica. Un insieme è una collezione di oggetti o elementi che hanno qualcosa in comune, ovvero che rispettano tutti la stessa proprietà. Questi elementi possono essere numeri, lettere, persone, oggetti, o qualsiasi altra cosa. Gli insiemi sono spesso rappresentati tra parentesi graffe, come ad esempio {1, 2, 3} che è un insieme di numeri.
Possono esistere delle relazioni tra due insiemi. Di cosa si tratta? Gli elementi di due insiemi possono avere un legame, quindi li colleghiamo con una freccia. La freccia esprime la relazione che esiste tra i due insiemi. Un altro modo per rappresentare una relazione è una tabella a doppia entrata: segniamo con una croce gli elementi che hanno un legame, quindi che sono legati dalla relazione.
Scopriamo insieme come rappresentare le relazioni tra insiemi!
- A cosa servono le frecce negli insiemi
- Frecce e relazioni
- Altri esempi di relazioni
- Relazioni con la tabella a doppia entrata
A cosa servono le frecce negli insiemi

Le frecce sono simboli molto utilizzati in matematica! E no, non servono per tirare con l’arco!
Sono strumenti utili per rappresentare delle proprietà o delle relazioni tra elementi matematici.
Frecce e relazioni
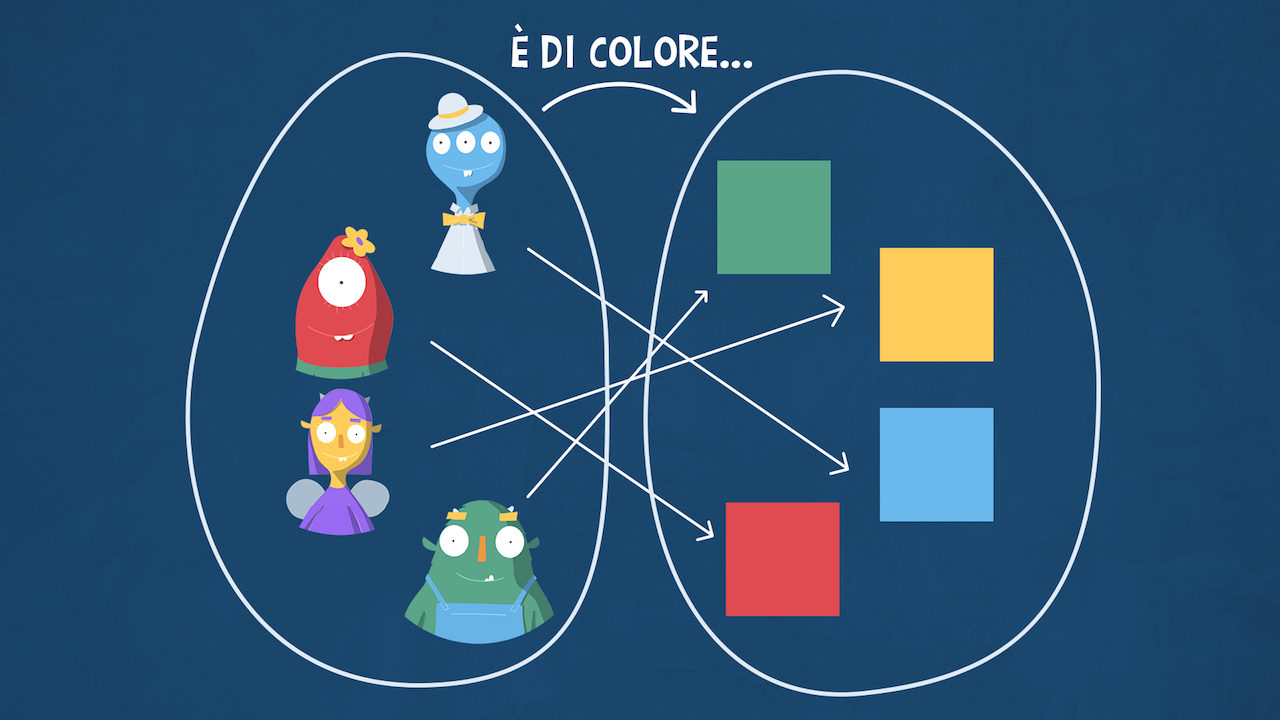
Relazione “è di colore”
Relazione “meno 5”
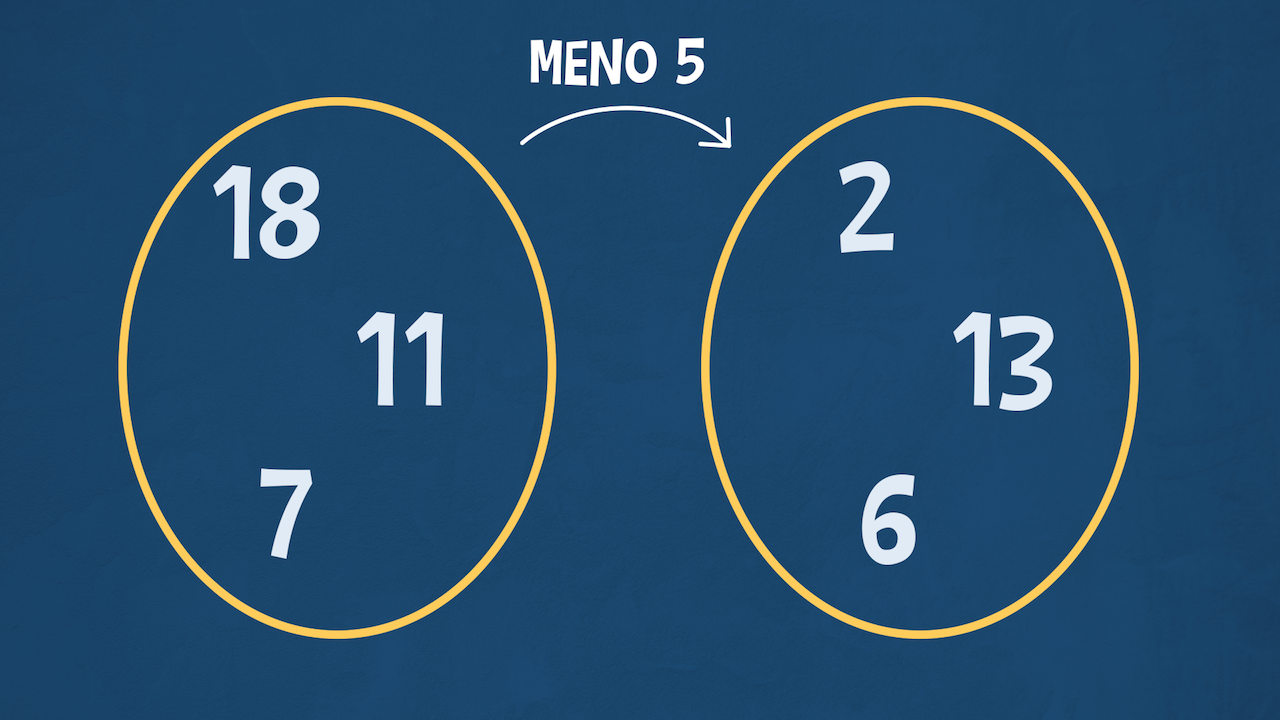
Per indicare una relazione tra due elementi di due insiemi, possiamo utilizzare una freccia che collega questi due elementi.
Collegando due elementi, indichiamo che esiste una relazioni tra di essi, un legame. La freccia indica questa relazione, assumendo un significato diverso di volta in volta.
Osserva l’esempio: la freccia rappresenta la relazione “è di colore”.
Prova tu a risolvere il secondo esempio: quali numeri sono collegati con la freccia che indica la relazione “meno 5”?
Altri esempi di relazioni
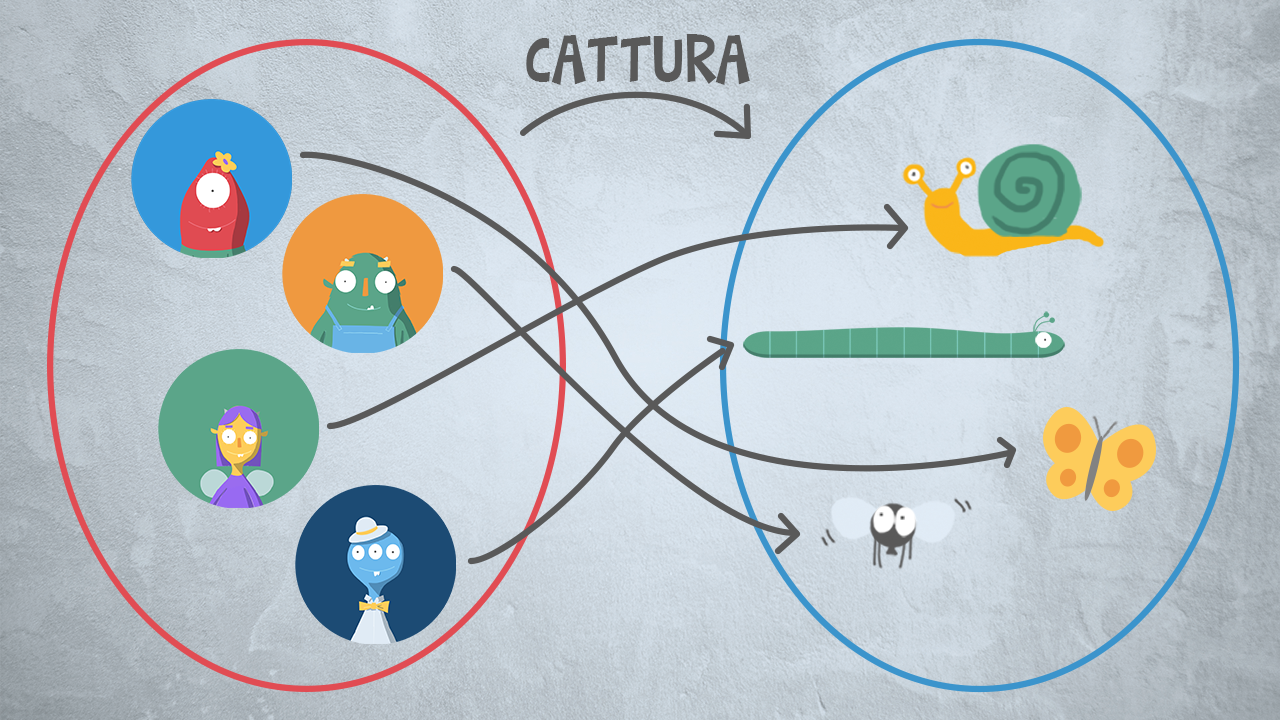
Relazione “cattura”
Relazione inversa “è catturato da”

Il significato della relazione cambia se cambia il verso della freccia.
Osserva l’esempio: è disegnata la relazione “cattura”. Infatti Oscar cattura le mosche, Lisa cattura le farfalle e così via.
Cambiando il verso della freccia, possiamo rappresentare la relazione inversa: “è catturato da”. Così nell’esempio vediamo che le mosche sono catturate da Oscar, le farfalle sono catturate da Lisa, e così via.
Abbinamento di numeri e i loro doppi
Abbiamo due insiemi:
- Insieme X: {1, 2, 3}
- Insieme Y: {2, 4, 6}
Vogliamo mostrare la relazione tra ogni numero e il suo doppio:
- 1 → 2
- 2 → 4
- 3 → 6
Ogni numero dell’insieme X è collegato al suo doppio nell’insieme Y tramite una freccia.
Abbinamento di bambini e i loro giocattoli preferiti
Immaginiamo due insiemi:
- Insieme C: {Anna, Luca, Maria}
- Insieme D: {palla, bambola, camion}
Vogliamo mostrare quale giocattolo preferisce ogni bambino:
- Anna → bambola
- Luca → camion
- Maria → palla
In questo caso, ogni bambino è collegato al suo giocattolo preferito tramite una freccia.
Abbinamento di giorni della settimana e le attività
Abbiamo due insiemi:
- Insieme G: {Lunedì, Martedì, Mercoledì}
- Insieme H: {scuola, calcio, musica}
Vogliamo mostrare l’attività principale di ogni giorno:
- Lunedì → scuola
- Martedì → calcio
- Mercoledì → musica
Ogni giorno della settimana è collegato alla sua attività principale tramite una freccia.
Relazioni con la tabella a doppia entrata

Possiamo rappresentare una relazione anche con una tabella a doppia entrata.
Cos’è la tabella a doppia entrata? È composta da righe e colonne, dove ciascuna riga e ciascuna colonna rappresentano una delle due variabili. I dati vengono inseriti nelle celle della tabella, che si trovano all’intersezione di una riga e di una colonna. Questo tipo di tabella è particolarmente utile per confrontare e analizzare informazioni in modo chiaro e sistematico.
Inseriamo gli elementi del primo insieme nella prima colonna della tabella, gli elementi del secondo insieme nella prima riga della tabella. Per rappresentare quali elementi di ciascun insieme sono in relazione tra loro, indichiamo con una X la casella di corrispondenza dei due elementi.
Relazione “è di colore”
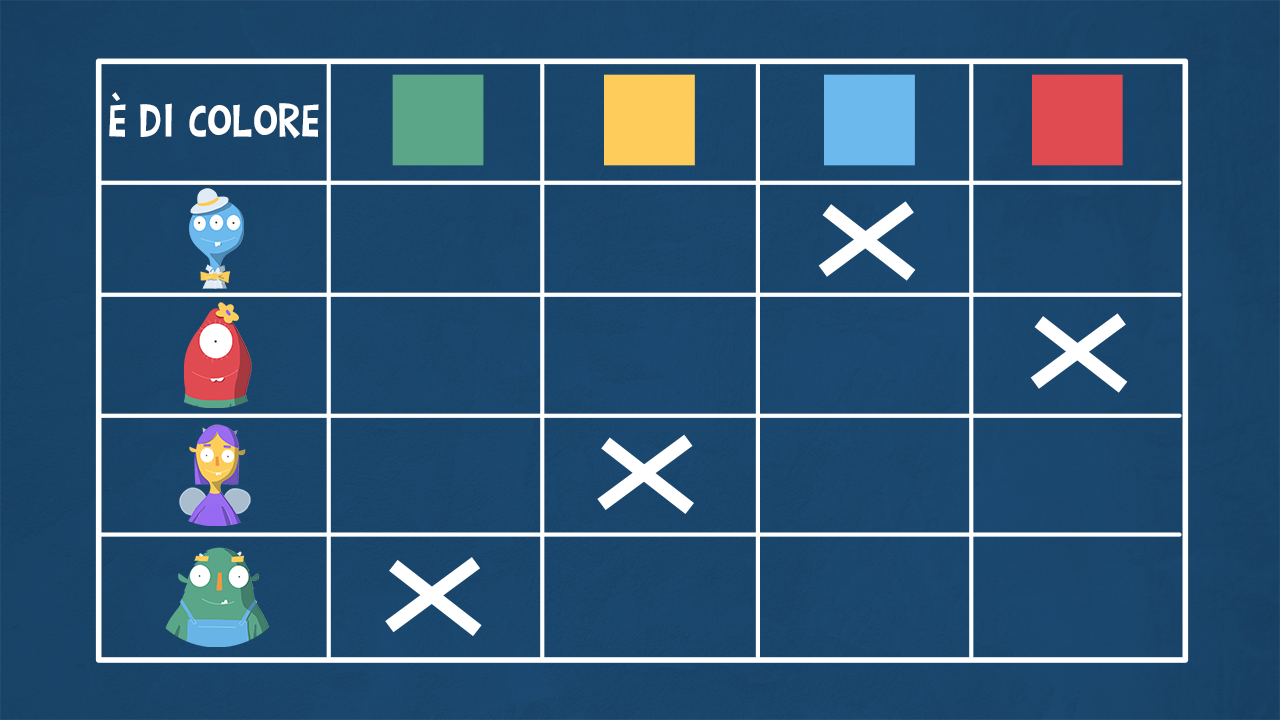
Rappresentiamo gli elementi del primo insieme nella prima colonna, quelli del secondo insieme nella prima riga. Inseriamo una X nella casella giusta per indicare gli elementi che sono in relazione tra loro, seguendo la relazione indicata dalla freccia, cioè “è di colore”.
Relazione “meno 5”

Prova a completare la seconda tabella per rappresentare la relazione “meno 5”.
Questo tipo di rappresentazione ci sarà utile nello studio della probabilità e per altri argomenti che scoprirai più avanti negli anni.
