Operazioni e proprietà degli insiemi
Gli insiemi matematici rappresentano uno dei pilastri fondamentali del mondo della matematica, influenzando vari campi di studio e fornendo strumenti per comprendere relazioni e strutturazioni.
Questo articolo ti guiderà attraverso le proprietà degli insiemi, le loro caratteristiche principali e le operazioni fondamentali, per consentirti di comprendere e applicare la teoria degli insiemi.
- Cos'è un insieme in matematica
- Le caratteristiche degli insiemi complementari
- Le proprietà e le operazioni degli insiemi matematici
- Il prodotto cartesiano tra due insiemi
- Le proprietà e le operazioni tra insiemi
Cos’è un insieme in matematica
Un insieme è, in termini semplici, una raccolta o collezione di oggetti, noti come elementi. Questi oggetti possono spaziare dai numeri interi, ai simboli, a concetti più astratti come i colori o le idee. L’importante è che all’interno di un insieme, ogni elemento sia unico e non ripetuto.
Avvicinandoci al concetto dei sottoinsiemi, possiamo pensare a questi come insiemi “minoritari” rispetto ad un insieme di riferimento. Un sottoinsieme contiene elementi che sono esclusivamente presi dall’insieme di riferimento.
Se un sottoinsieme contiene tutti gli elementi dell’insieme ma non ha elementi extra, è un sottoinsieme improprio. Se, al contrario, contiene alcuni ma non tutti gli elementi dell’insieme, viene definito sottoinsieme proprio.
Le caratteristiche degli insiemi complementari
Gli insiemi complementari hanno una relazione specifica tra loro. Se consideriamo un insieme universale U, ogni insieme A all’interno di U avrà un complementare, spesso denotato come A’, che comprende tutti gli elementi di U che non appartengono ad A.
Ad esempio, se U rappresenta l’insieme di tutti gli animali e A l’insieme degli uccelli, A’ rappresenterà tutti gli animali che non sono uccelli. Le caratteristiche degli insiemi complementari risiedono nella loro capacità di “completare” l’insieme originale rispetto all’insieme universale di riferimento, senza alcuna sovrapposizione di elementi.
Le proprietà e le operazioni degli insiemi matematici
Ogni insieme, grazie alla sua struttura, può essere manipolato attraverso una serie di operazioni fondamentali. L’unione insiemi rappresenta la combinazione degli elementi di due o più insiemi, eliminando eventuali ripetizioni.
L’intersezione, invece, identifica gli elementi comuni tra due insiemi. La differenza tra insiemi mostra gli elementi presenti in un insieme ma non nell’altro, mentre il complemento di un insieme, come già accennato, contiene gli elementi non presenti in quello insieme rispetto a un insieme universale.
Queste operazioni non solo definiscono le proprietà degli insiemi, ma ne influenzano anche l’utilizzo in contesti pratici, come la risoluzione di problemi o l’analisi di dati.
Il prodotto cartesiano tra due insiemi
Il prodotto cartesiano tra due insiemi A e B consiste nell’elencare tutte le possibili coppie ordinate di elementi provenienti da A e B. Ad esempio, dati gli insiemi A = {1, 2} e B = {a, b}, il prodotto cartesiano risultante sarà {(1, a), (1, b), (2, a), (2, b)}. Questa operazione è particolarmente utile in situazioni che richiedono la considerazione di tutte le possibili combinazioni tra gli elementi di due insiemi, come nell’analisi combinatoria, nello studio di relazioni e funzioni, e in molti altri ambiti matematici avanzati.
Le proprietà e le operazioni tra insiemi
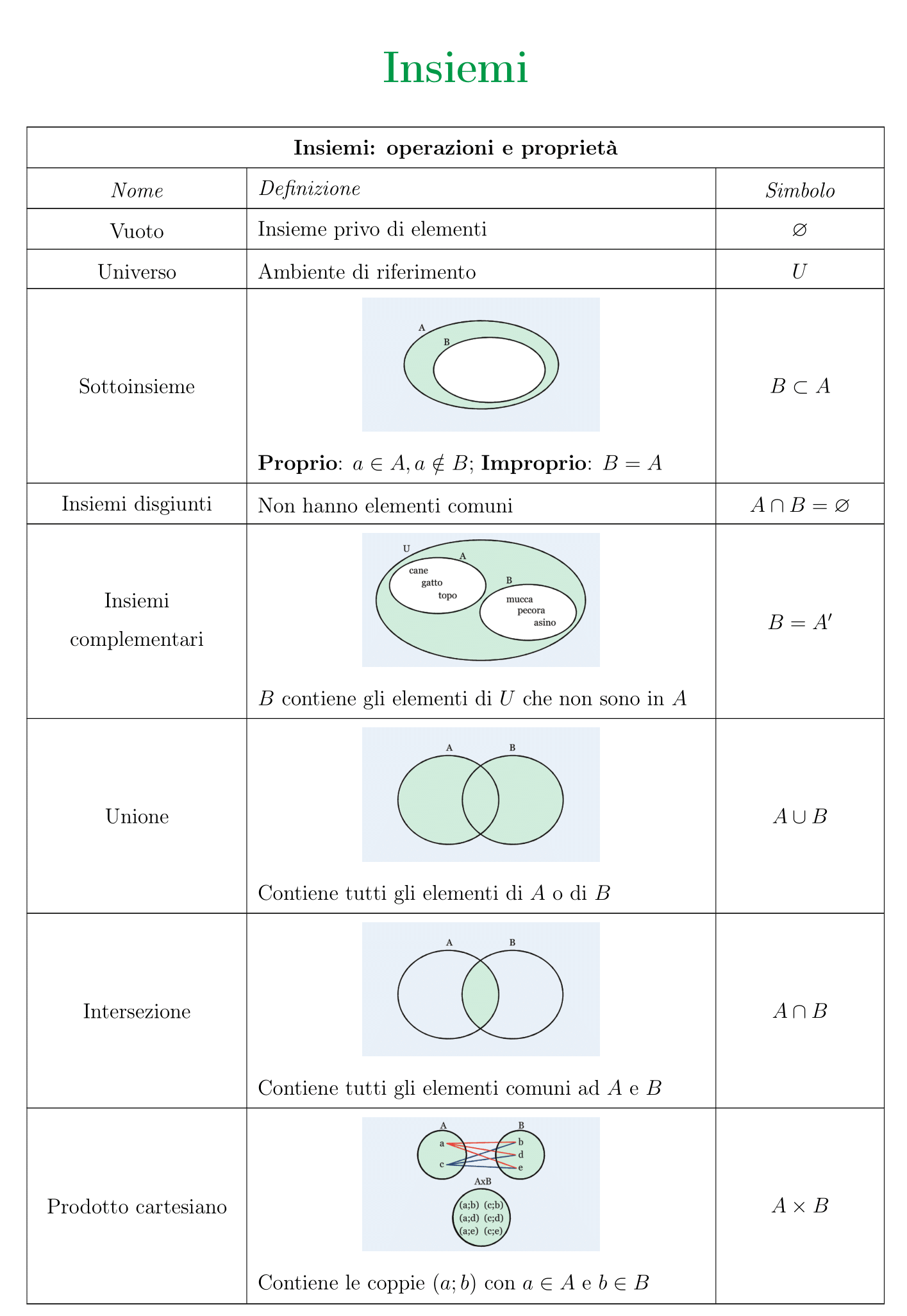
Adesso che hai imparato cos’è un insieme e quali sono le sue caratteristiche principali, sei pronto a ripassare utilizzando la nostra tabella! Troverai tutte le nozioni che abbiamo trattato e potrai utilizzarla per ripetere tutto più velocemente!
