Aree poligoni: tutte le formule

L’area di un poligono è rappresentata dalla superficie interna del poligono, cioè la porzione di piano racchiusa all’interno dei lati del poligono.

In questo articolo troverai tutte le formule per calcolare l’area dei poligoni: dall’area del rettangolo a quella del parallelogramma e del quadrato, insieme anche ad una tabella riassuntiva che ti aiuterà soprattutto durante la fase del ripasso prima delle verifiche o delle interrogazioni.

Scopri quali sono le formule dirette per calcolare l’area del parallelogramma, del rettangolo, del quadrato, del trapezio, dei poligoni con diagonali perpendicolari! Vedrai anche le formule inverse così non avrai più dubbi negli esercizi di geometria piana.

Infine, trovi anche una tabella riassuntiva, che ti aiuterà soprattutto durante la fase del ripasso prima delle verifiche o delle interrogazioni.

In questa lezione troverai le formule dell’area e le formule inverse di:

• quadrato
• parallelogramma e rettangolo
• quadrilateri con diagonali perpendicolari
• trapezio

• Area del rettangolo e del parallelogramma
• Area del quadrato
• Area dei quadrilateri con le diagonali perpendicolari
• Area del triangolo
• Area del trapezio
• Area dei poligoni regolari
• Tabella perimetri e aree

Area del rettangolo e del parallelogramma

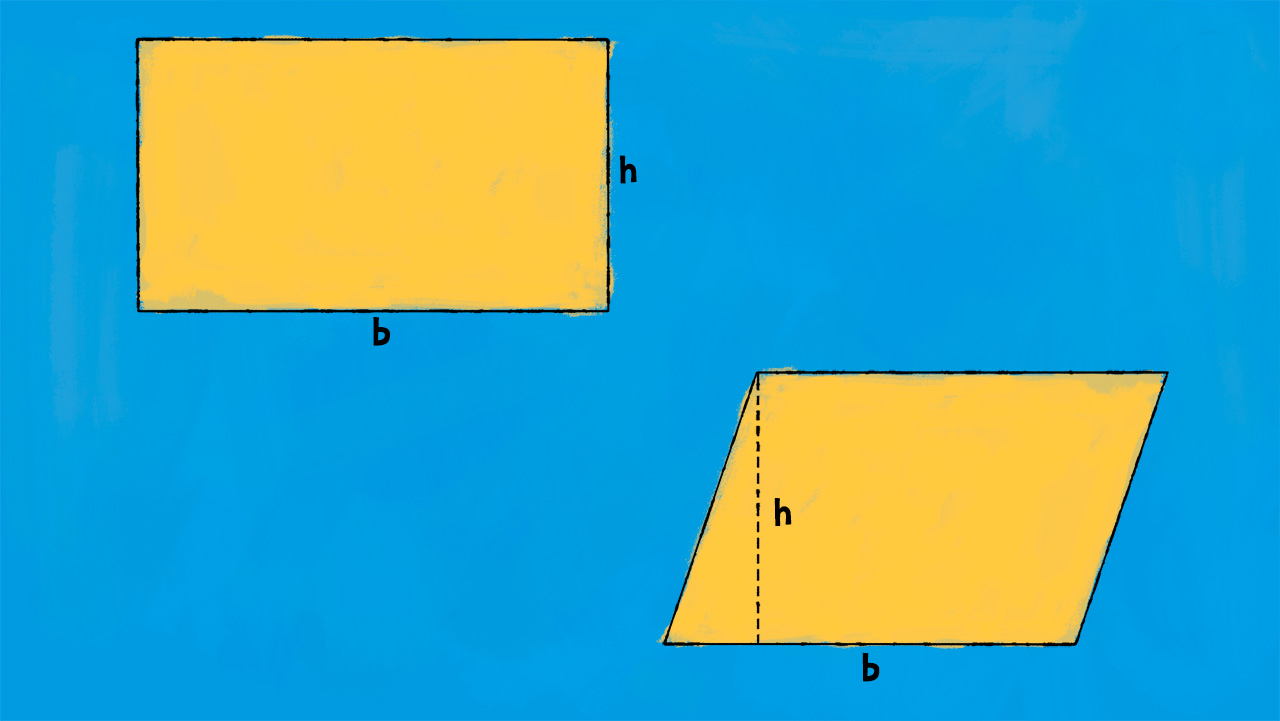
Un rettangolo è un tipo di quadrilatero che ha le seguenti proprietà:

• Angoli Retti: Tutti e quattro gli angoli interni di un rettangolo sono angoli retti, cioè misurano 90 gradi.
• Lati Opposti Paralleli e Uguali: Ogni coppia di lati opposti in un rettangolo è sia parallela che uguale in lunghezza.
• Simmetrie: Un rettangolo ha una simmetria bilaterale; può essere diviso in due parti speculari sia attraverso l’asse che collega i lati opposti sia attraverso quello che collega i mezzi dei lati più lunghi.
• Diagonali: Le diagonali di un rettangolo sono uguali in lunghezza e si dividono scambievolmente a metà.

Un parallelogramma è un altro tipo di quadrilatero e ha queste caratteristiche distintive:

• Lati Opposti Paralleli: In un parallelogramma, ogni coppia di lati opposti è parallela.
• Lati Opposti Uguali: Le lunghezze dei lati opposti in un parallelogramma sono uguali.
• Angoli Opposti Uguali: Gli angoli opposti in un parallelogramma sono uguali.
• Diagonali: Le diagonali di un parallelogramma si dividono scambievolmente in due parti, ma non sono necessariamente uguali.
• Angoli Consecutivi Supplementari: Ogni coppia di angoli consecutivi in un parallelogramma è supplementare, cioè la loro somma è di 180 gradi.

Formula diretta:

£$ A = b \cdot h $£

Formule inverse:

£$ b = \frac{A}{h} $£ £$ h = \frac{A}{b} $£

Area del quadrato

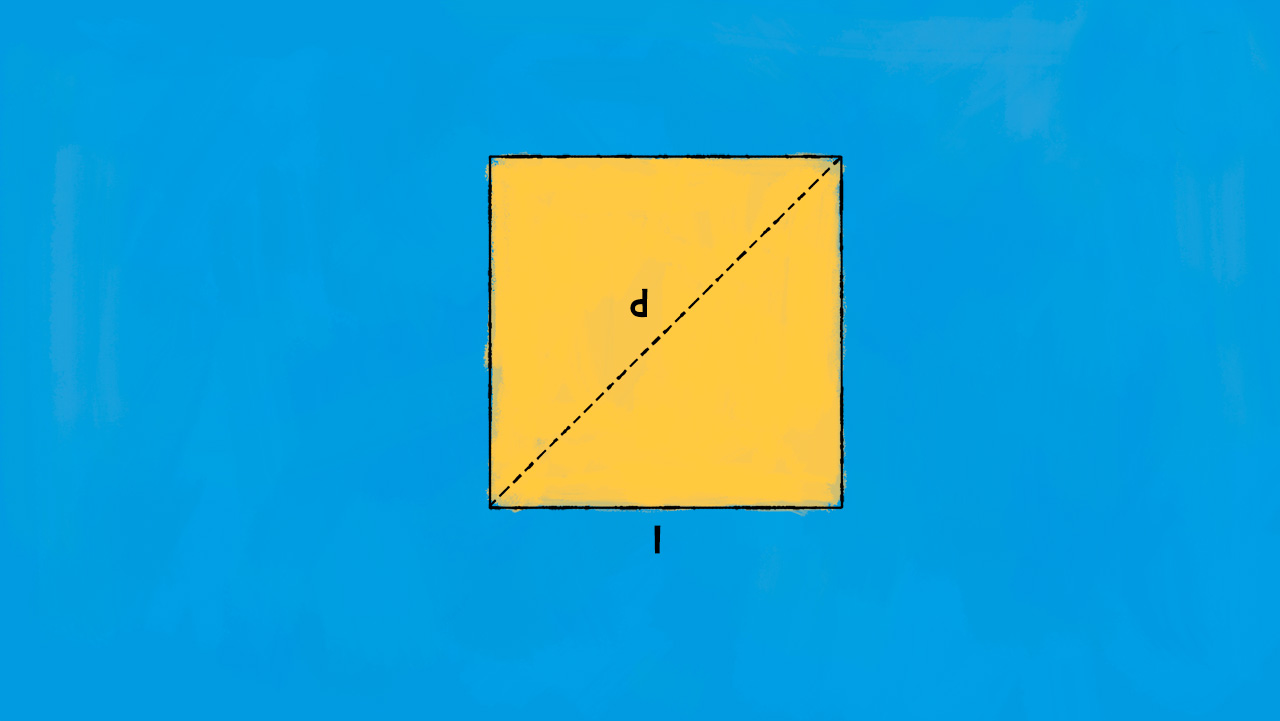
Il quadrato è un tipo particolare di quadrilatero, molto speciale e regolare, che gode di diverse proprietà matematiche e geometriche fondamentali. Ecco le caratteristiche distintive di un quadrato:

1. Lati Uguali: Tutti e quattro i lati di un quadrato hanno la stessa lunghezza.
2. Angoli Retti: Ogni angolo interno di un quadrato è un angolo retto, vale a dire 90 gradi.
3. Simmetria: Il quadrato ha una simmetria assiale rispetto alle linee che congiungono i mezzi dei lati opposti e anche rispetto alle diagonali. Questo lo rende altamente simmetrico rispetto ad altre forme.
4. Diagonali: Le diagonali di un quadrato sono uguali in lunghezza e si intersecano a metà, dividendo ciascuna diagonale in due parti uguali. Inoltre, queste diagonali sono perpendicolari tra loro.
5. Circonferenza circoscritta: Il quadrato può essere inscritto in una circonferenza in modo che tutti e quattro i suoi vertici tocchino la circonferenza. Questo cerchio è chiamato cerchio circoscritto e il suo centro è il punto di intersezione delle diagonali del quadrato.
6. Proprietà di rotazione: Ruotando un quadrato di 90 gradi attorno al suo centro, otteniamo una figura che è identica alla figura originale, mostrando la sua simmetria rotazionale.

Formule dirette:

£$ A = l^2 $£

oppure

£$ A = \frac{d^2}{2} $£

Formule inverse:

£$ l = \sqrt{A} $£

oppure

£$ d = \sqrt{2A} $£

Area dei quadrilateri con le diagonali perpendicolari

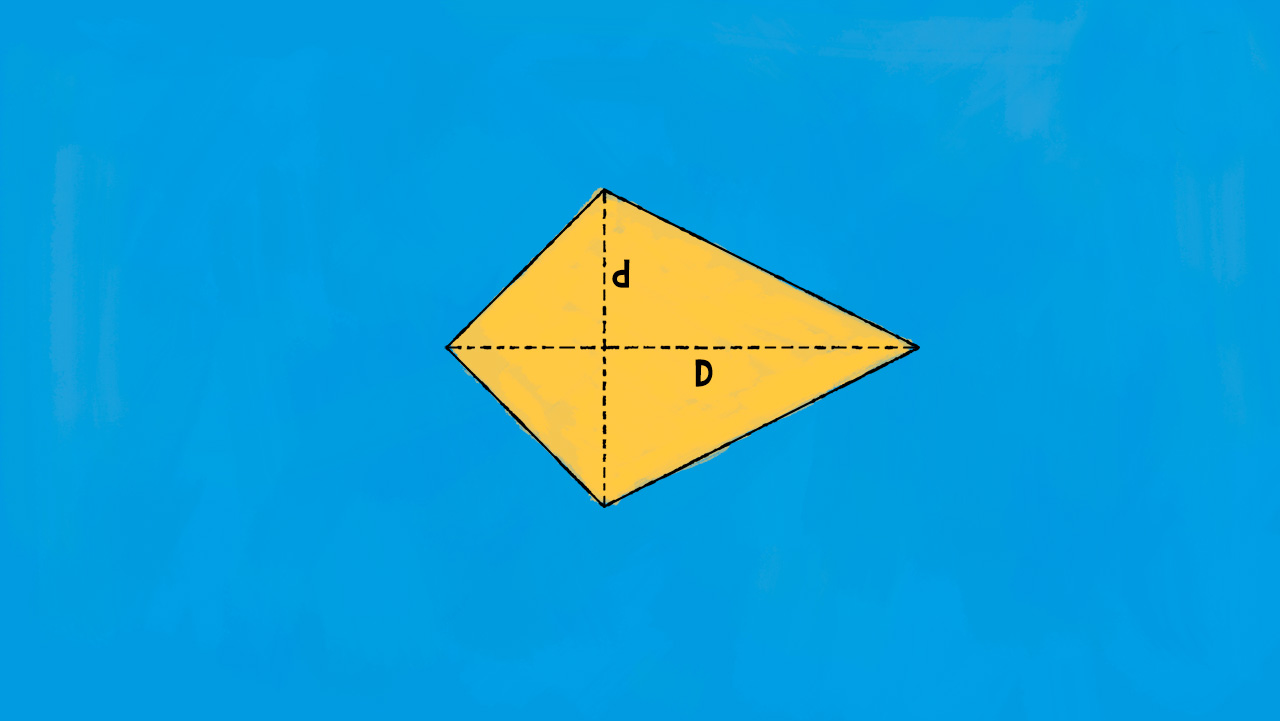
Formula diretta:

£$ A = \frac{D \cdot d}{2} $£

Formule inverse:

£$ D = \frac{2A}{d} $£ £$ d = \frac{2A}{D} $£

Area del triangolo

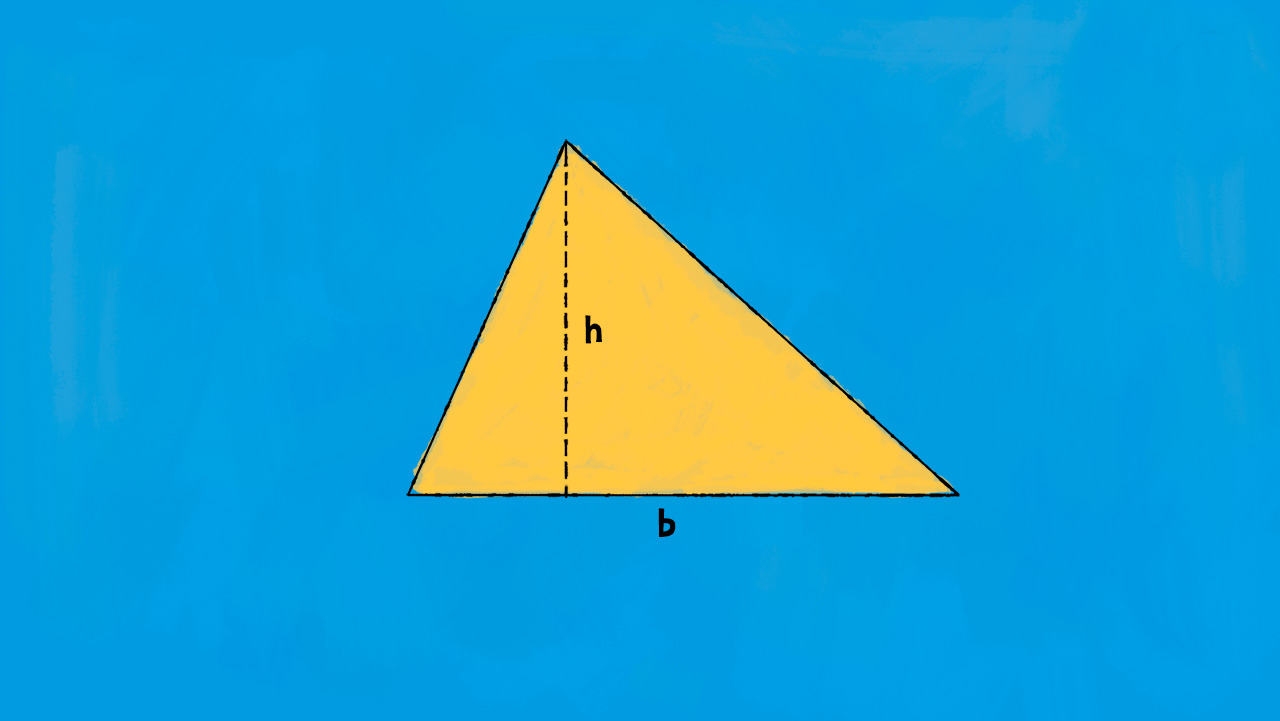
Il triangolo è una delle forme geometriche più elementari e fondamentali in matematica. Si tratta di un poligono con tre lati e tre angoli. I triangoli possono essere classificati in base a diversi criteri:

• In base alla lunghezza dei lati:
  • Equilatero: Tutti e tre i lati hanno la stessa lunghezza.
  • Isoscele: Due lati hanno la stessa lunghezza.
  • Scaleno: Tutti e tre i lati hanno lunghezze diverse.
• In base agli angoli:
  • Acutangolo: Tutti gli angoli sono acuti (meno di 90 gradi).
  • Rettangolo: Un angolo è retto (90 gradi).
  • Ottusangolo: Un angolo è ottuso (più di 90 gradi).

Formula diretta:

£$ A = \frac{b \cdot h}{2} $£

Formule inverse:

£$ b = \frac{2A}{h} $£ £$ h = \frac{2A}{b} $£

Area del trapezio

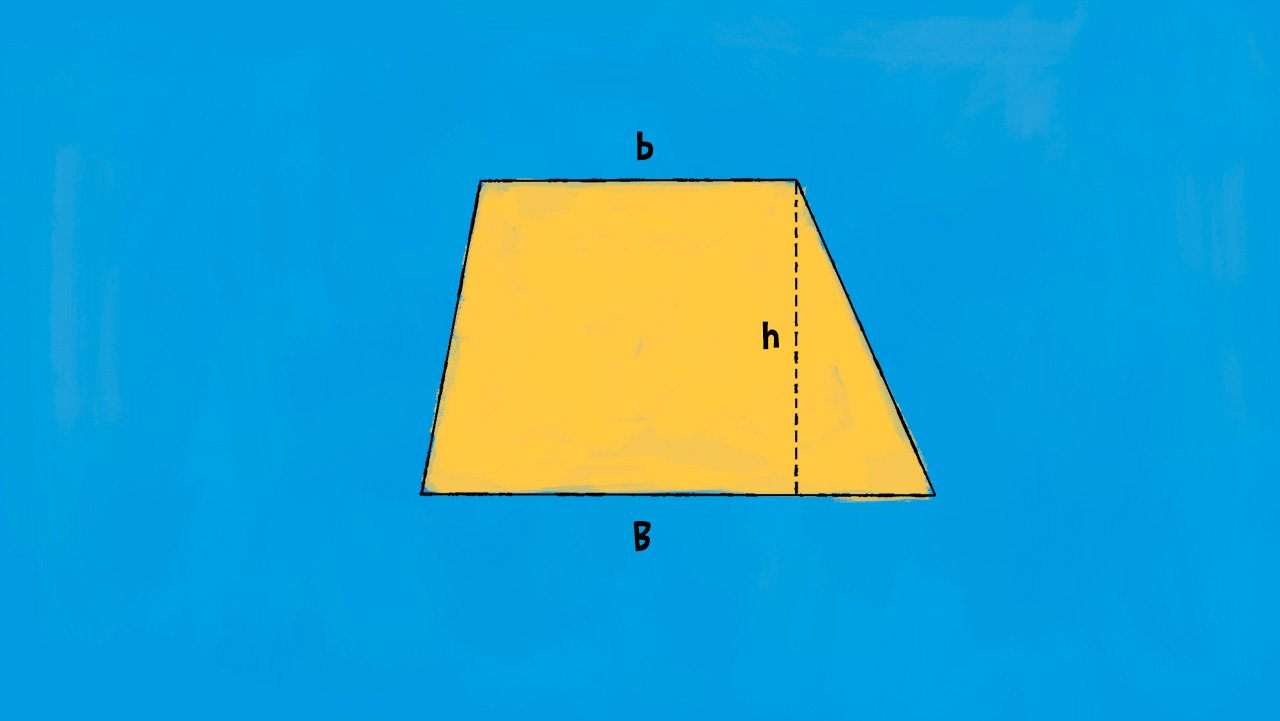
Il trapezio è un altro tipo di quadrilatero, noto per avere una coppia di lati opposti paralleli, chiamati basi, mentre gli altri due lati non sono paralleli e vengono chiamati lati non paralleli o gambe. A seconda delle caratteristiche specifiche, i trapezi possono essere ulteriormente classificati in:

• Trapezio isoscele: I lati non paralleli sono uguali in lunghezza e gli angoli adiacenti a ciascuna base sono uguali. Questa simmetria conferisce al trapezio isoscele proprietà uniche, simili a quelle di un triangolo isoscele.
• Trapezio rettangolo: Uno o entrambi i lati non paralleli sono perpendicolari alle basi.

Formula diretta:

£$ A = \frac{(B + b)\cdot h}{2} $£

Formule inverse:

£$ B = \frac{2A}{h} – b $£ £$ b = \frac{2A}{h} – B $£

Area dei poligoni regolari

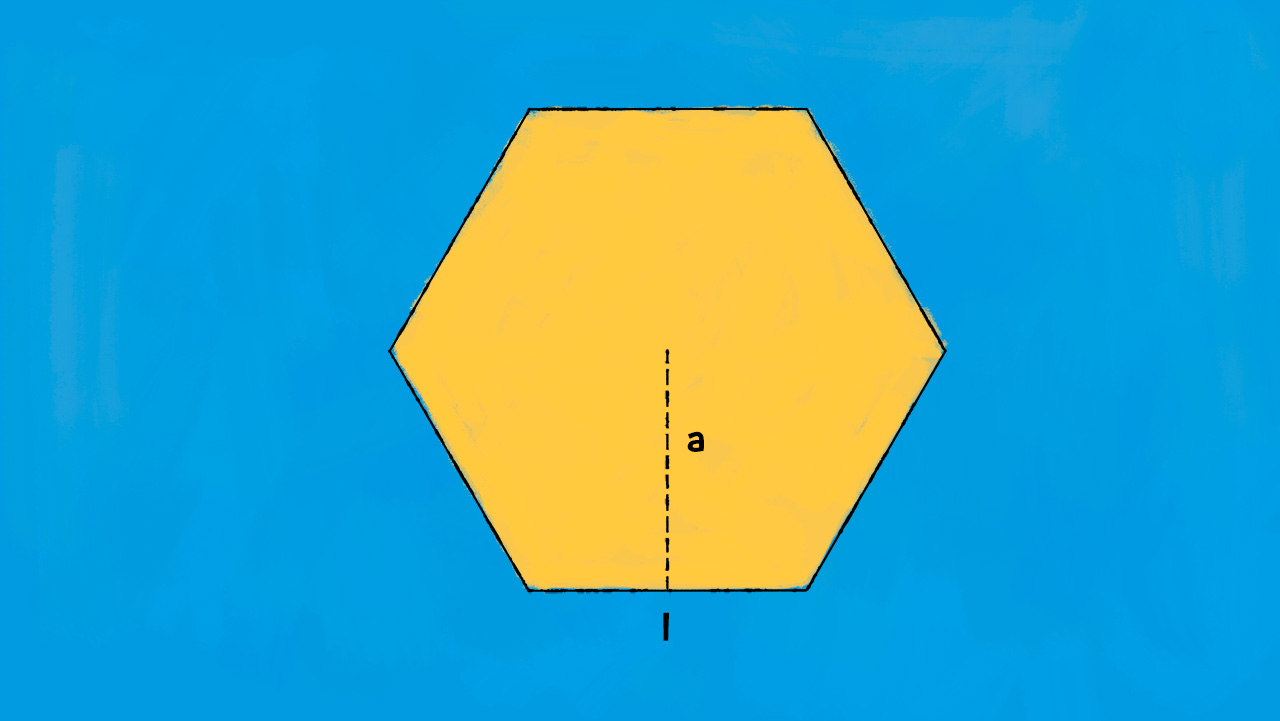
Formula diretta:

£$ A = \frac{\text{perimetro} \cdot \text{apotema}}{2} = \frac{p \cdot a}{2} $£

Formule inverse:

£$ p = \frac{2A}{a} $£ £$ a = \frac{2A}{p} $£

Tabella perimetri e aree

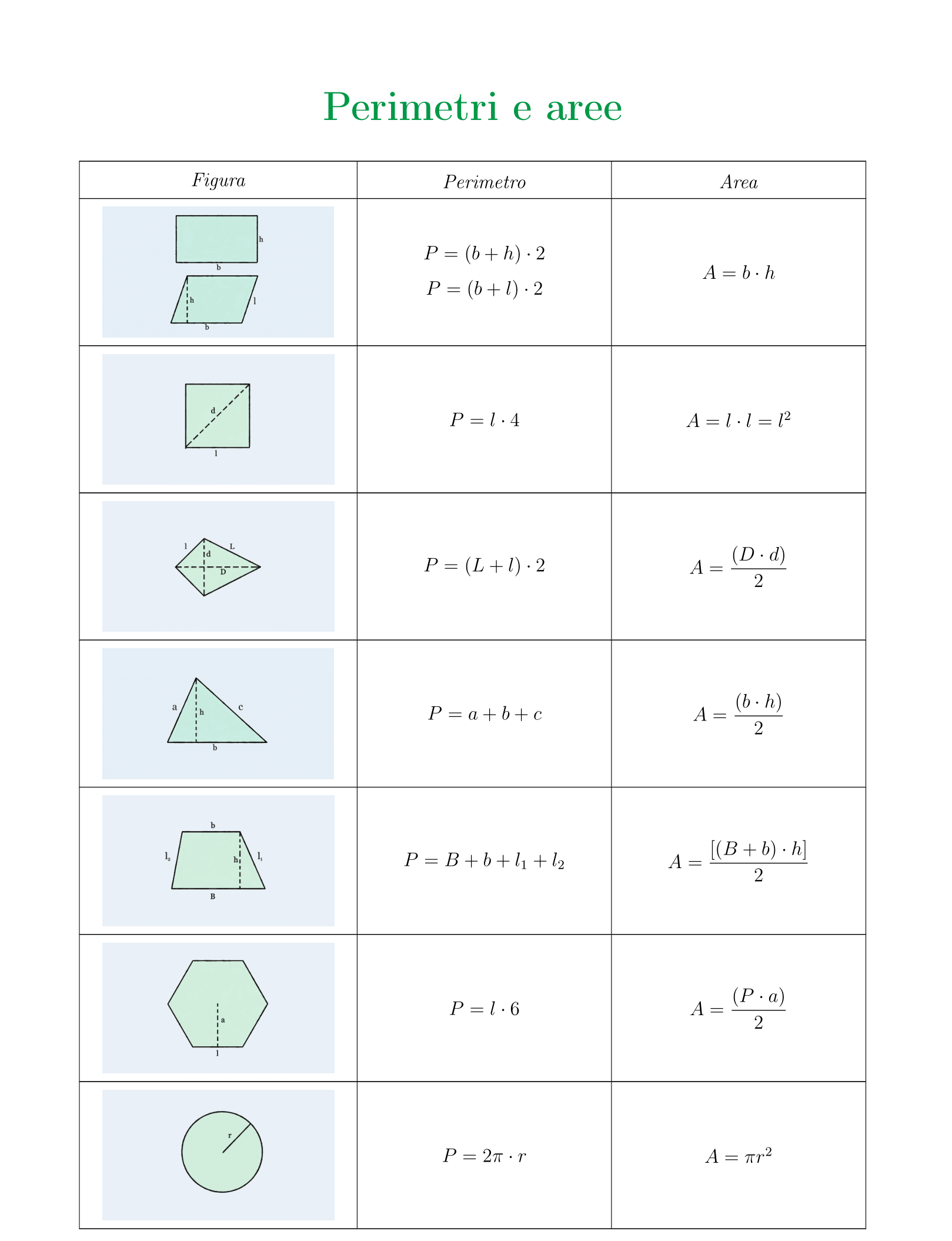
Tutte le formule per il perimetro e l’area di poligoni raccolte in una tabella riassuntiva, così non avrai di che temere prima dell’interrogazione o della verifica!