Le figure equivalenti ed equiscomponibili: cosa sono
La matematica non si limita alla risoluzione di equazioni o al calcolo di numeri, ma estende la sua portata anche alla comprensione delle forme, delle loro proprietà e della loro interrelazione grazie all’intreccio con la geometria. In questo articolo, esploreremo il concetto di figure equivalenti e equiscomponibili, due principi fondamentali che regolano le proprietà delle figure geometriche. Inoltre, ci avventureremo nel misterioso e intrigante universo del tangram, un antico puzzle cinese che combina abilmente questi due principi.
Il mondo è pieno di forme e figure, dalle strutture architettoniche alle opere d’arte, dai disegni nei libri di testo alle illustrazioni nei libri per bambini. Comprendere il concetto di figure equivalenti ed equiscomponibili è molto importante per capire come le forme si collegano e interagiscono l’una con l’altra.
Scopriamo insieme cosa significano questi termini!
Cosa sono le figure equivalenti
Cosa si intende precisamente per figure equivalenti? Si tratta di figure che, pur avendo forme diverse, condividono la stessa area. Questo concetto può essere facilmente visualizzato immaginando di avere due fogli di carta della stessa dimensione ma di forma diversa, uno quadrato e l’altro triangolare, per esempio. Nonostante la loro evidente differenza estetica, se confrontassimo le loro aree, scopriremmo che sono perfettamente equivalenti.
Ma perché questo è importante? Beh, il concetto di equivalenza è un principio fondamentale nella risoluzione di problemi che riguardano l’area e il perimetro in geometria, le operazioni su integrali in calcolo e persino nel campo della fisica, dove le aree vengono utilizzate per rappresentare quantità fisiche come il lavoro o l’energia.
Cosa sono le figure equiscomponibili
Ora, passiamo alle figure equiscomponibili. Questo termine un po’ tecnico si riferisce a figure che, nonostante possano sembrare diverse, possono essere suddivise in un numero finito di parti che, opportunamente riarrangiate, consentono di formare un’altra figura. Questo concetto è strettamente correlato all’idea di equivalenza, ma spinge la comprensione un passo avanti, introducendo l’idea che non solo l’area, ma anche la forma può essere preservata attraverso una serie di trasformazioni geometriche.
Pensa, per esempio, a un puzzle. I singoli pezzi, sebbene distinti e unici, possono essere riorganizzati per formare un’immagine complessiva. Questa è l’essenza delle figure equiscomponibili. E, proprio come i puzzle, anche le figure equiscomponibili possono essere usate per affinare le competenze di problem solving, potenziare il ragionamento spaziale e anche per esplorare e comprendere concetti più avanzati come la simmetria e la conservazione.
Tangram e aree di poligoni
Il tangram è un antico gioco cinese che combina in modo magistrale i concetti di figure equivalenti ed equiscomponibili. Il tangram è composto da sette pezzi geometrici: cinque triangoli di tre dimensioni diverse, un quadrato e un parallelogramma. L’obiettivo è utilizzare tutti questi pezzi per creare una serie di figure predeterminate, senza sovrapposizioni o intersezioni.
Maneggiando i pezzi, girandoli e capovolgendoli, i giocatori possono visualizzare come le figure si adattano insieme, come l’area viene conservata attraverso una serie di trasformazioni, e come forme diverse possono emergere dall’organizzazione di pezzi identici. Così, mentre ci divertiamo, sviluppiamo anche una profonda comprensione dei concetti matematici alla base del gioco!
Il perimetro è la misura del contorno di una figura e la sua unità di misura è il £$\text{m}$£ (con multipli e sottomultipli). Come si chiama la parte racchiusa dentro al perimetro? È la parte di piano che occupa la nostra figura, cioè la sua superficie. La misura della superficie di una figura è l’area. L’unità di misura dell’area è il £$\text{m}^2$£ (con i suoi multipli e sottomultipli).
Le figure che hanno lo stesso perimetro si chiamano isoperimetriche, quelle con la stessa area, invece, sono equivalenti.
Il tangram è un quadrato scomposto in £$7$£ forme geometriche con le quali puoi costruire figure diverse. Le figure che formi con i pezzi del tangram si chiamano equiscomponibili perché sono composte da figure equivalenti e congruenti fra loro!
Qual è l’unità di misura dell’area
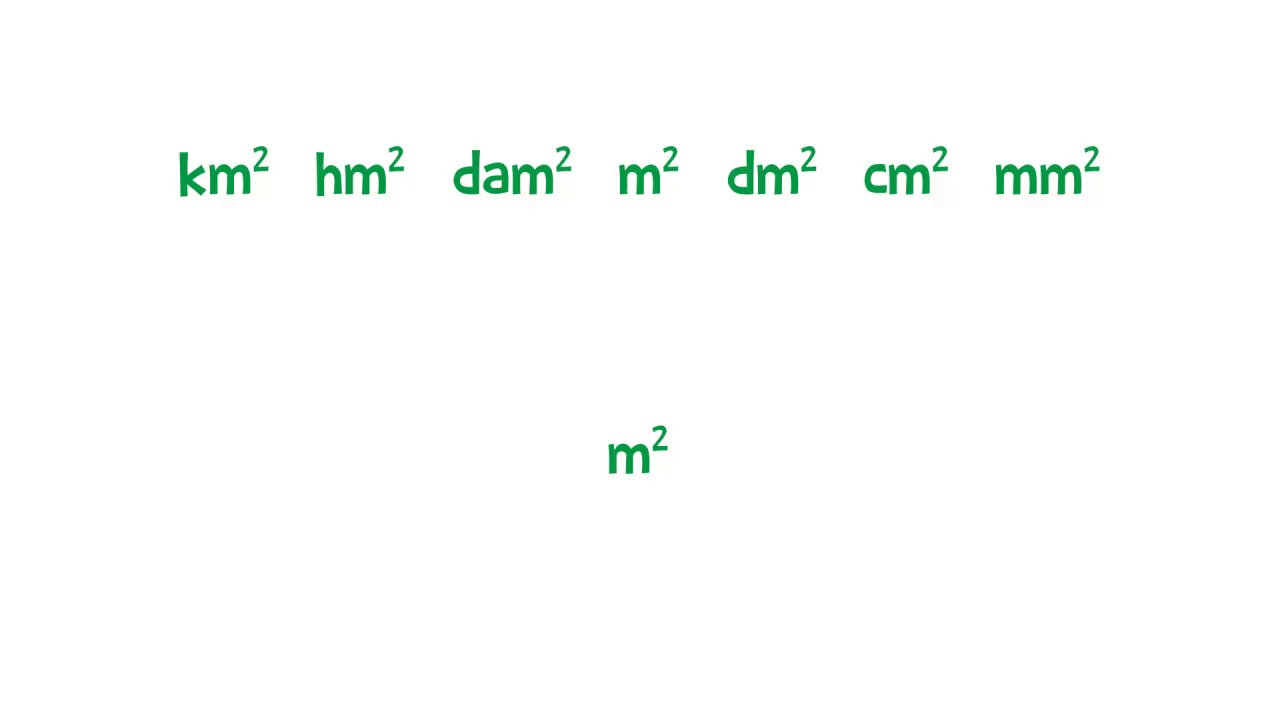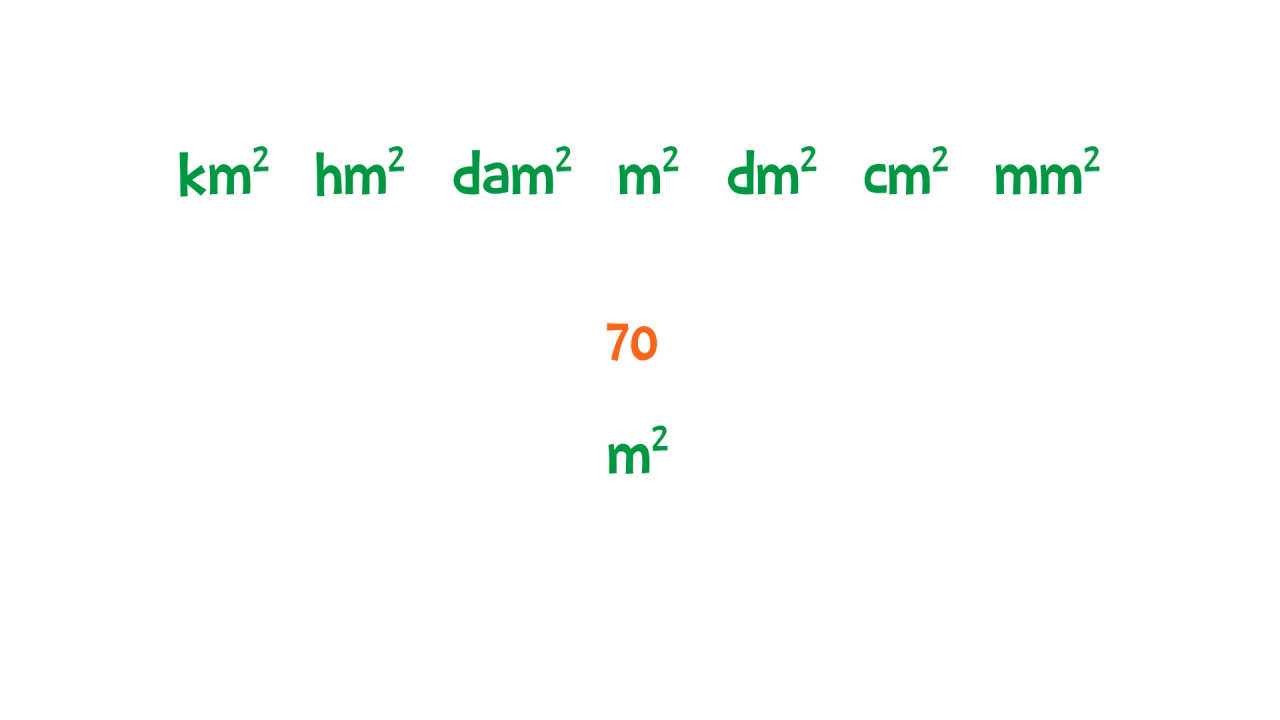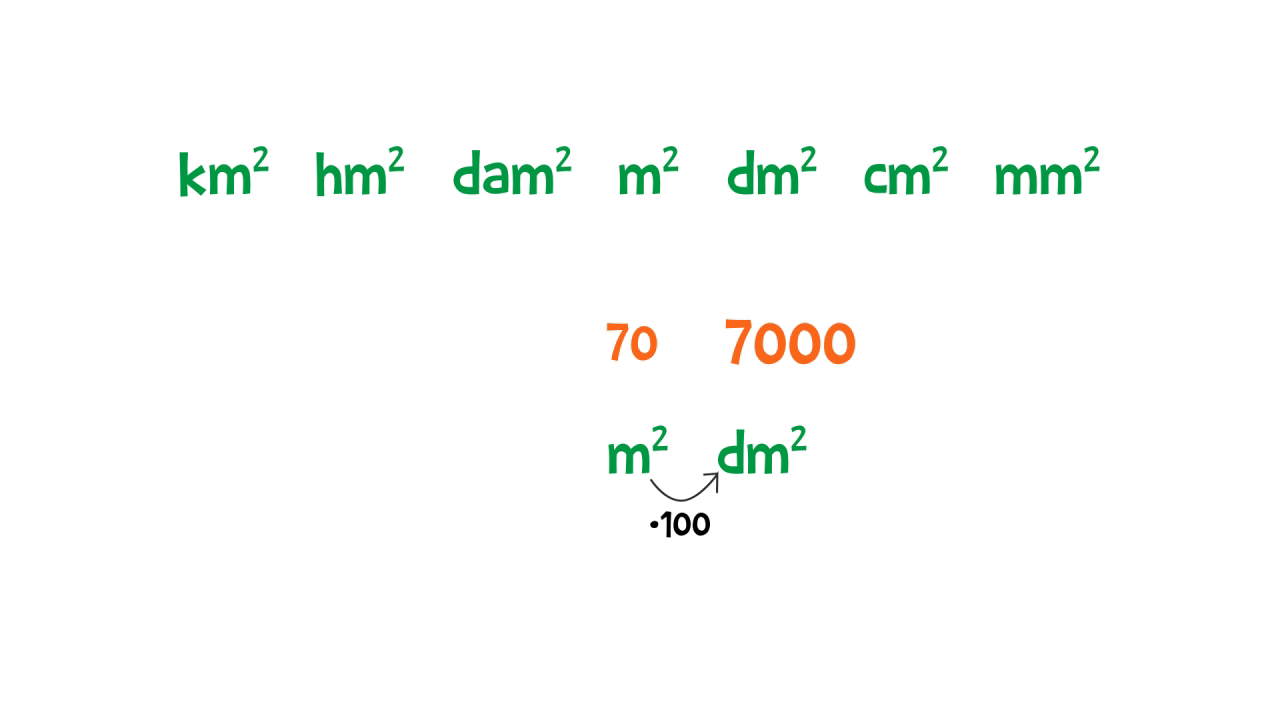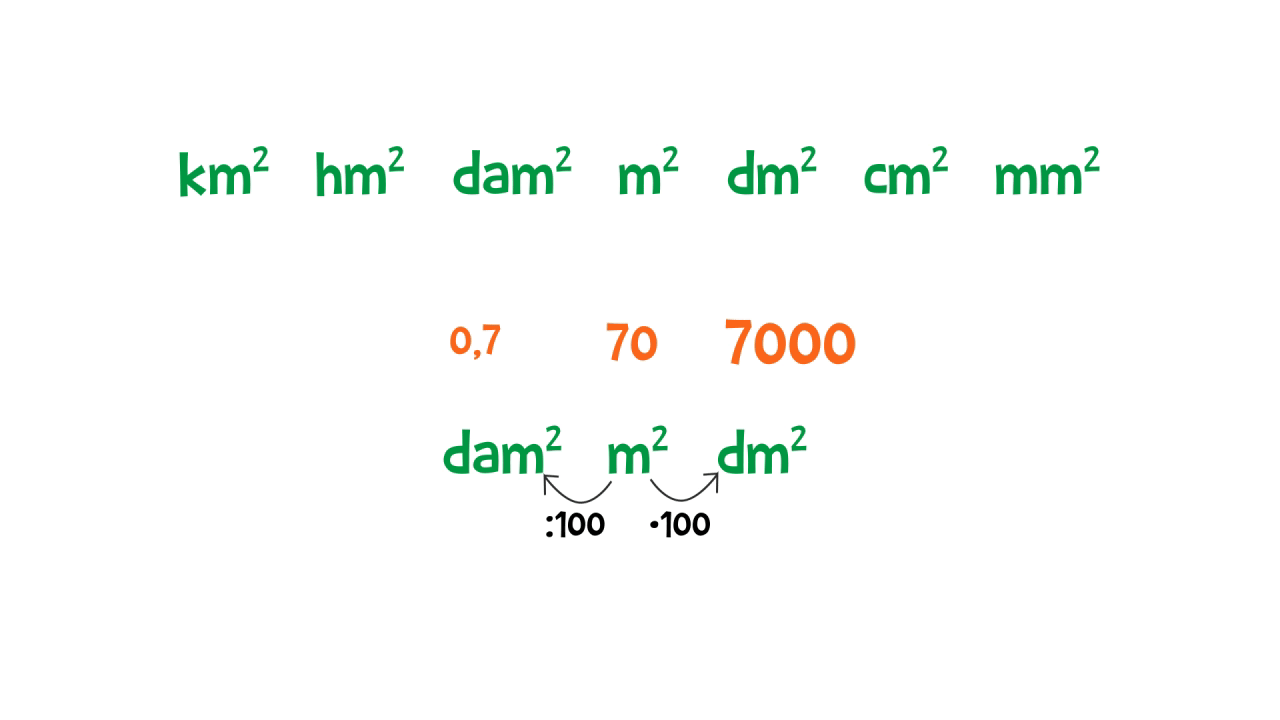
Il perimetro si calcola sommando la misura di tutti i lati di una figura. La sua unità di misura è il metro, oppure uno dei suoi sottomultipli. Per passare da una misura all’altra devi moltiplicare o dividere per £$10$£ tante volte quante sono le “posizioni" di cui ti muovi.
Ti ricordi? Chiediamoci cosa accade per la misura delle superfici, cioè per le aree.
Per calcolare le aree utilizziamo delle moltiplicazioni. Quindi, come abbiamo detto studiando le potenze particolari, dobbiamo moltiplicare anche le unità di misura. Ecco perché l’unità di misura fondamentale per misurare l’area è il metro quadrato £$\text{m}^2$£. Ci troviamo di fronte a delle misure quadrate: ogni volta che passiamo da una misura all’altra dobbiamo moltiplicare o dividere per £$100$£ e non per £$10$£, infatti £$10^2=100$£.
Esempio: l’area del nostro oggetto misura £$3 \text{ m}^2 = 3 \cdot 100 \text{ dm}^2 = 300 \text{ dm}^2$£ oppure £$ 3 \text{ m}^2 = 3 : 100 \text{ dam}^2 = 0,03 \text{ dam}^2$£
Quando calcoli perimetro e area stai sempre attento a non mischiare le unità di misura! Fai sempre attenzione che le operazioni siano fatte tra grandezze omogenee, cioè che siano tutte espresse con la stessa unità di misura! Non puoi sommare una misura espressa in centimetri con una in kilometri!
