I poligoni: come calcolare perimetro e area
Il calcolo del perimetro e dell’area dei poligoni è un aspetto fondamentale della geometria. Il perimetro di un poligono si riferisce alla lunghezza totale dei suoi lati, una misura lineare che delinea il contorno della figura. L’area, invece, quantifica lo spazio bidimensionale racchiuso all’interno di questi confini, fornendo una misura della superficie del poligono.
I poligoni possono essere classificati in varie categorie, come triangoli, quadrilateri, pentagoni, ecc., in base al numero dei loro lati, e ciascuna categoria ha formule specifiche per il calcolo del perimetro e dell’area. Ad esempio, il perimetro di un poligono regolare, in cui tutti i lati e gli angoli sono uguali, può essere calcolato semplicemente moltiplicando la lunghezza di un lato per il numero totale dei lati, mentre l’area varia significativamente a seconda della forma specifica del poligono e richiede formule diverse per essere determinata accuratamente.
Per i poligoni regolari, esistono formule dirette che facilitano il calcolo dell’area, basate sul numero dei lati e sulla lunghezza di ciascuno. Per i poligoni irregolari, invece, il processo può essere più complesso e spesso richiede di dividere il poligono in figure più semplici, come triangoli, per i quali l’area può essere facilmente calcolata e poi sommata per ottenere l’area totale del poligono irregolare.
Vediamo come fare in linea generale a calcolare area e perimetro dei poligoni.
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Il perimetro dei poligoni: cos'è
- Perimetro dei poligoni regolari
- Apotema dei poligoni regolari
- Che cos'è l'area di un poligono
- L'unità di misura delle superfici
- Come si calcola l'area dei poligoni regolari
- Scheda attività - perimetri e aree
Il perimetro dei poligoni: cos’è

Cos’è il perimetro di una figura o di un poligono? Il perimetro è la lunghezza del contorno di un poligono.
Abbiamo imparato che i poligoni sono figure delimitate da una linea spezzata chiusa: la lunghezza di questa linea è il perimetro del poligono! Per trovarlo basta sommare le lunghezze di tutti i lati del poligono.
Questo concetto si applica a qualsiasi tipo di poligono, sia esso regolare (con tutti i lati e angoli uguali) sia irregolare (con lati e angoli di lunghezza e misura diverse).
Perimetro dei poligoni regolari
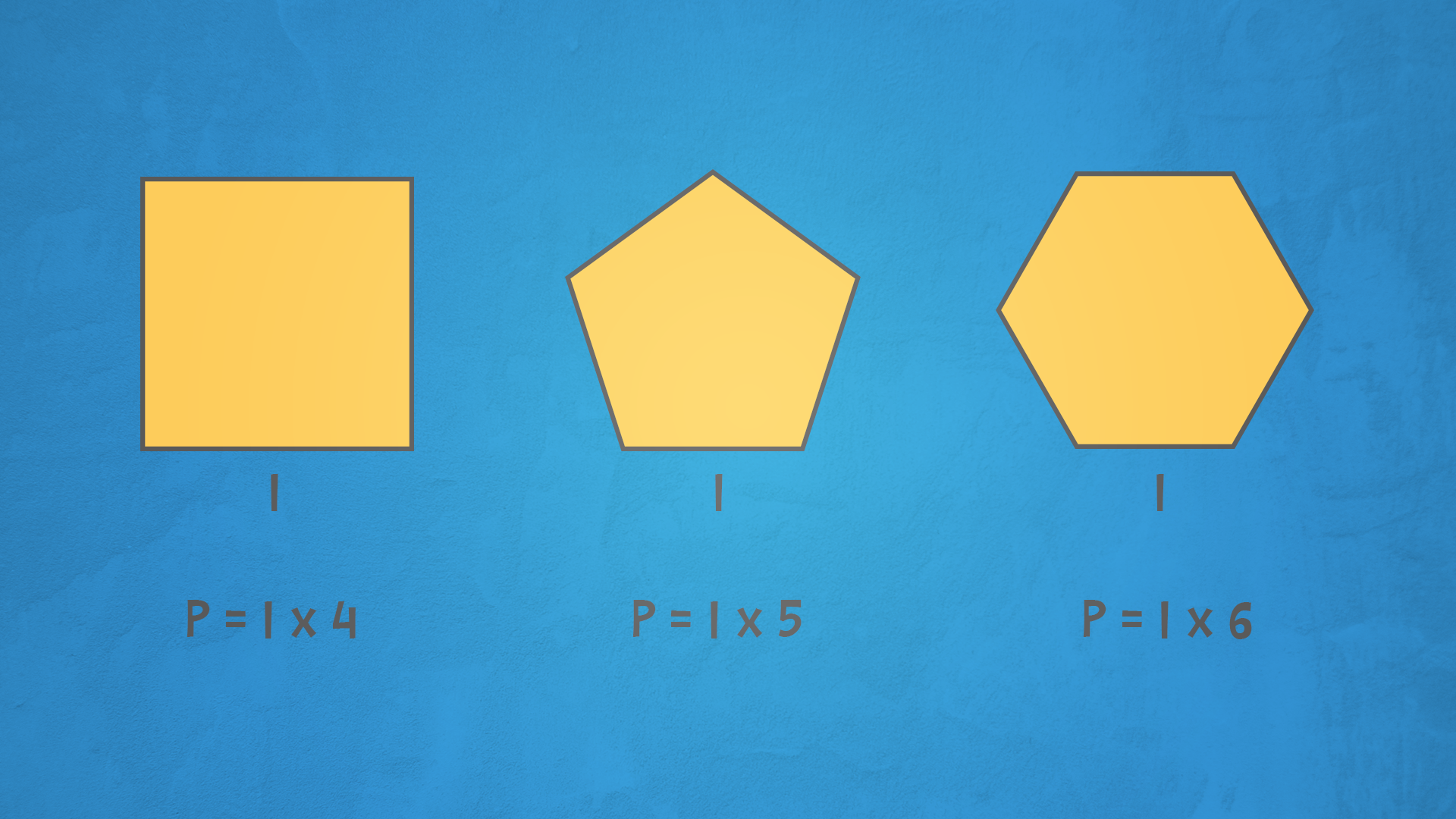
Trovare il perimetro dei poligoni regolari è facile! Se conosciamo il lato, basta moltiplicare la misura del lato per il numero di lati.
Indichiamo la misura del lato (l) e il numero di lati (n), ecco la misura del perimetro:
P = n x l
Ad esempio, il perimetro di un quadrato (un caso particolare di poligono regolare con quattro lati uguali) si calcola moltiplicando la lunghezza di un lato per quattro.
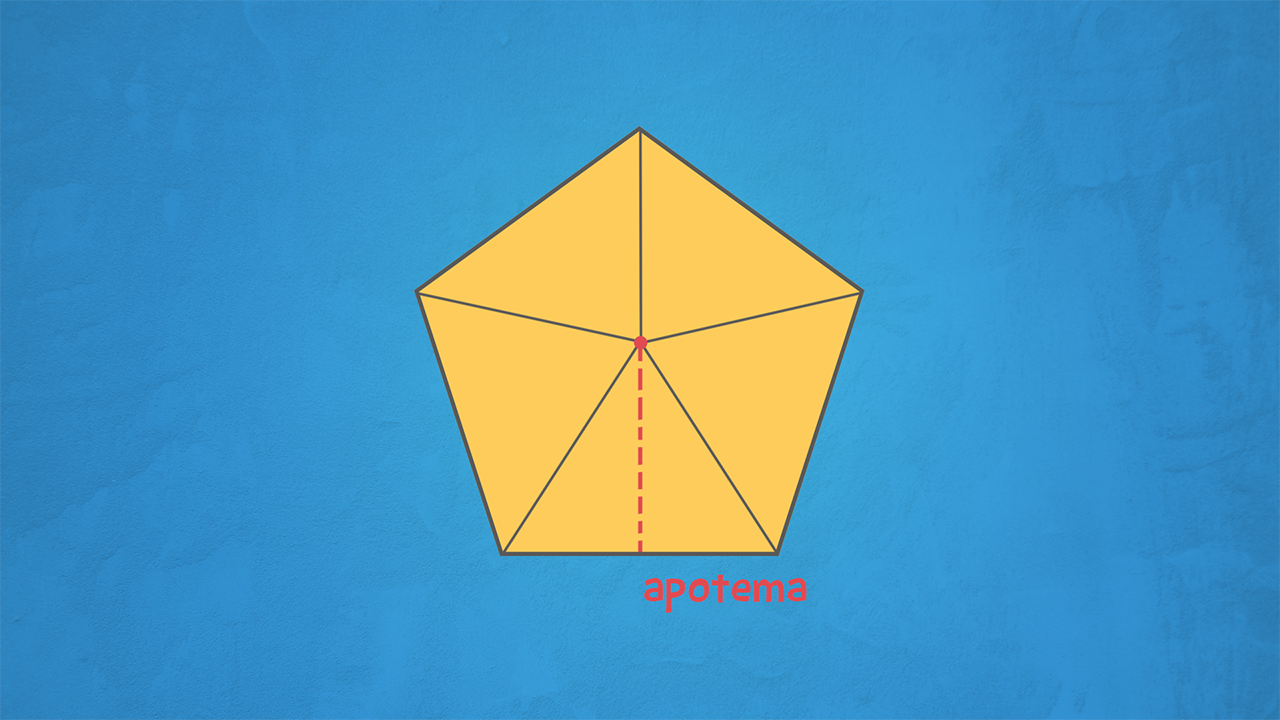
Apotema dei poligoni regolari
Apotema del pentagono
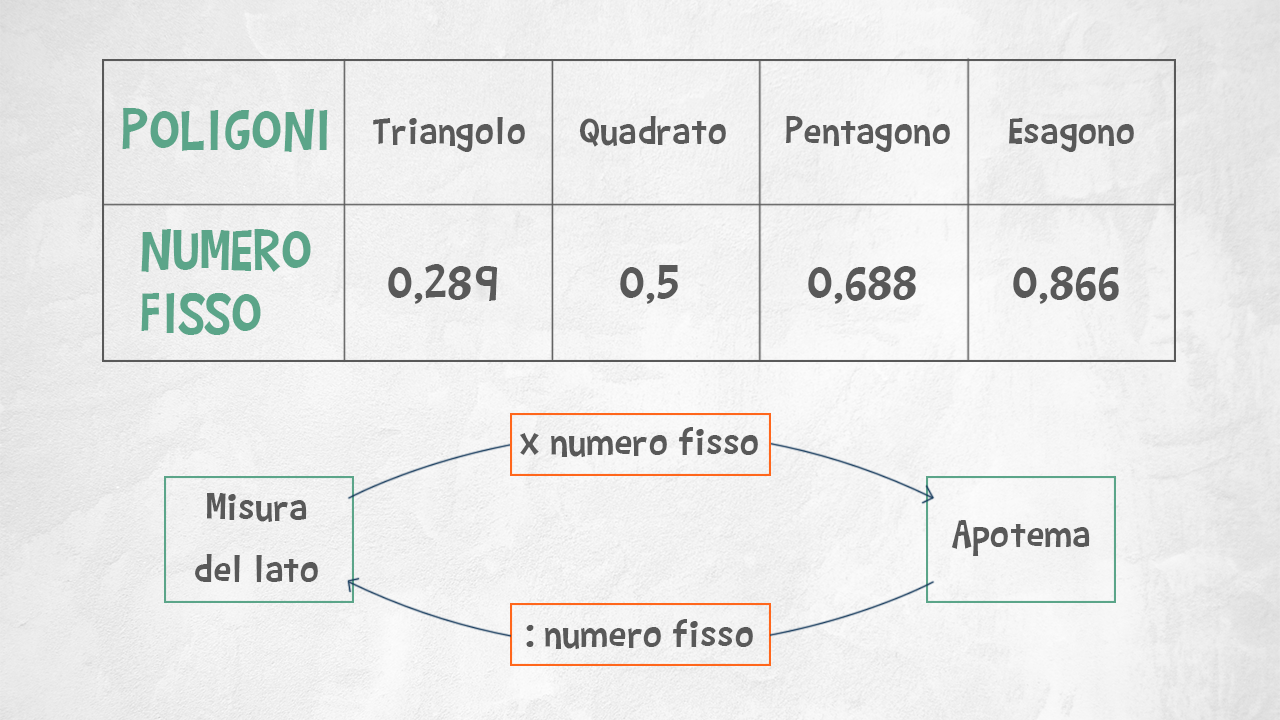
La tabella dei numeri fissi
Per calcolare l’area dei poligoni regolari ci serve un elemento nuovo, l’apotema.
I poligoni regolari hanno la particolarità di avere tutti i lati e tutti gli angoli uguali. Congiungendo i vertici dei lati con il centro del poligono, riusciamo a suddividere ciascun poligono regolare in triangoli isosceli tutti uguali, tanti quanti sono i lati del poligono regolare di partenza: troveremo 3 triangoli suddividendo il triangolo equilatero, 4 triangoli nel quadrato, 5 nel pentagono… e così via!
L’apotema è l’altezza di ciascuno di questi triangolini che riusciamo a ricavare in un poligono regolare.
Esiste un rapporto costante tra l’apotema e il lato dei poligoni che chiamiamo numero fisso.
Dividendo la misura dell’apotema del quadrato per la misura del suo lato otteniamo sempre 0,5: questo è il numero fisso del quadrato! Osserva la tabella per scoprire i numeri fissi che ti saranno più utili e la relazione che lega lato e apotema!
Che cos’è l’area di un poligono

L’area di un poligono è una misura che indica lo spazio occupato da quella figura sul piano.
Per calcolare la misura dell’area di un poligono dobbiamo trovare la sua superficie.
L’area è una quantità bidimensionale: possiamo disegnare un’area utilizzando un segmento come punta della nostra matita. Anche quando utilizziamo un evidenziatore, disegniamo un’area: è una linea spessa, che ha una lunghezza e un’altezza.
L’unità di misura delle superfici
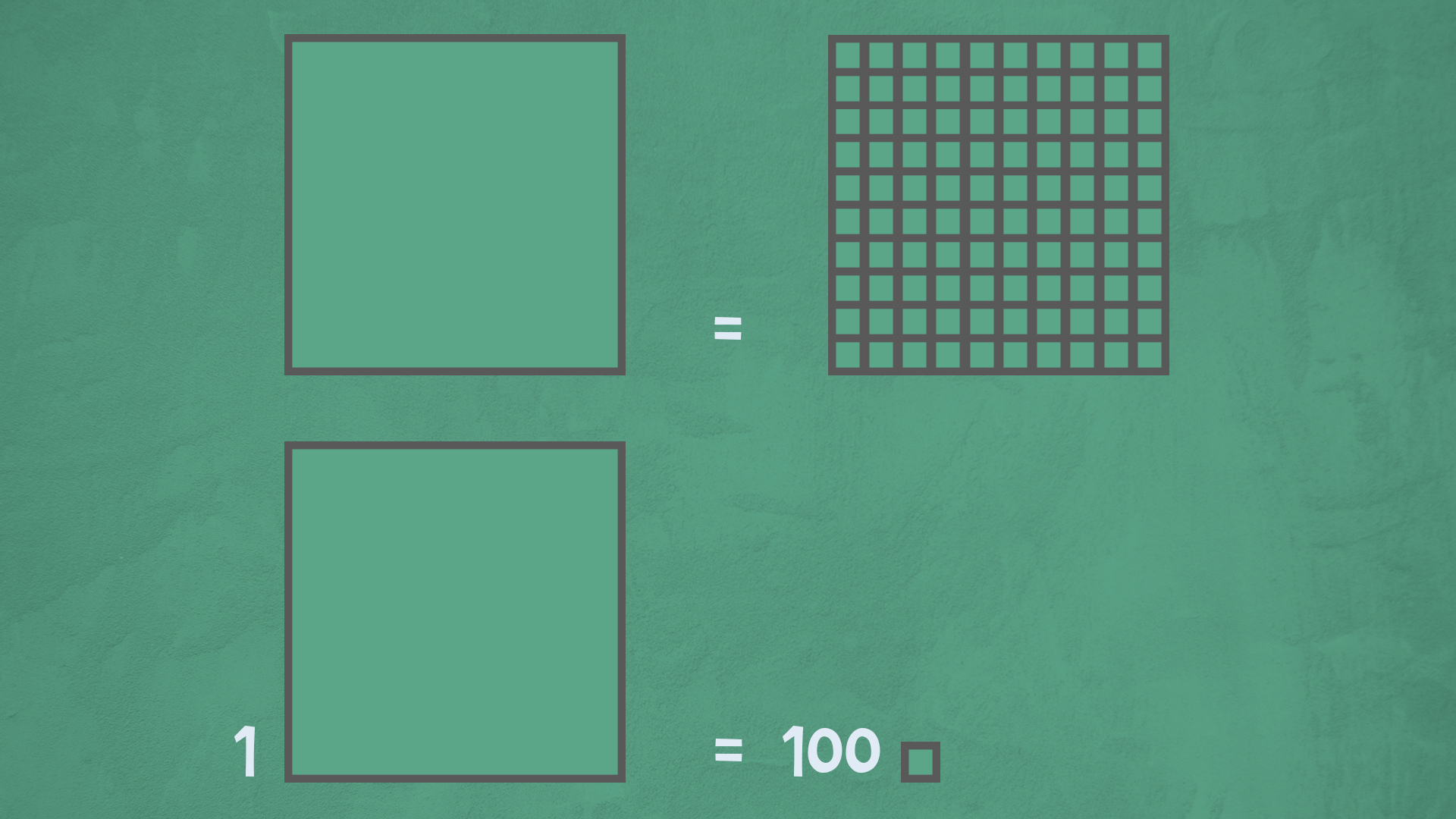
L’area è una quantità di due dimensioni: per calcolare l’area, infatti, prendiamo come riferimento una figura “unità" e vediamo quante volte è contenuta nella figura che stiamo analizzando. A seconda dell’unità di misura che scegliamo, otterremo dei risultati diversi.
Una superficie ha due dimensioni: non possiamo utilizzare la stessa unità di misura della lunghezza per misurarla. L’unità di misura delle aree è il metro quadrato (m£$^2$£) e corrisponde alla superficie di un quadrato con il lato di un metro.
Possiamo fare le equivalenze anche per le misure di superficie, ma dobbiamo fare attenzione: dato che sono misure quadratiche, per passare da un’unità di misura a quella immediatamente più piccola, dobbiamo moltiplicare per 100; per passare da un’unità di misura a quella immediatamente più grande, dobbiamo dividere per 100.
Esempio: 1 m£$^2$£ = 100 dm£$^2$£ e se passiamo a quella più grande abbiamo 1 m£$^2$£ = 0,01 dam£$^2$£
Unità di misura diverse, misure diverse
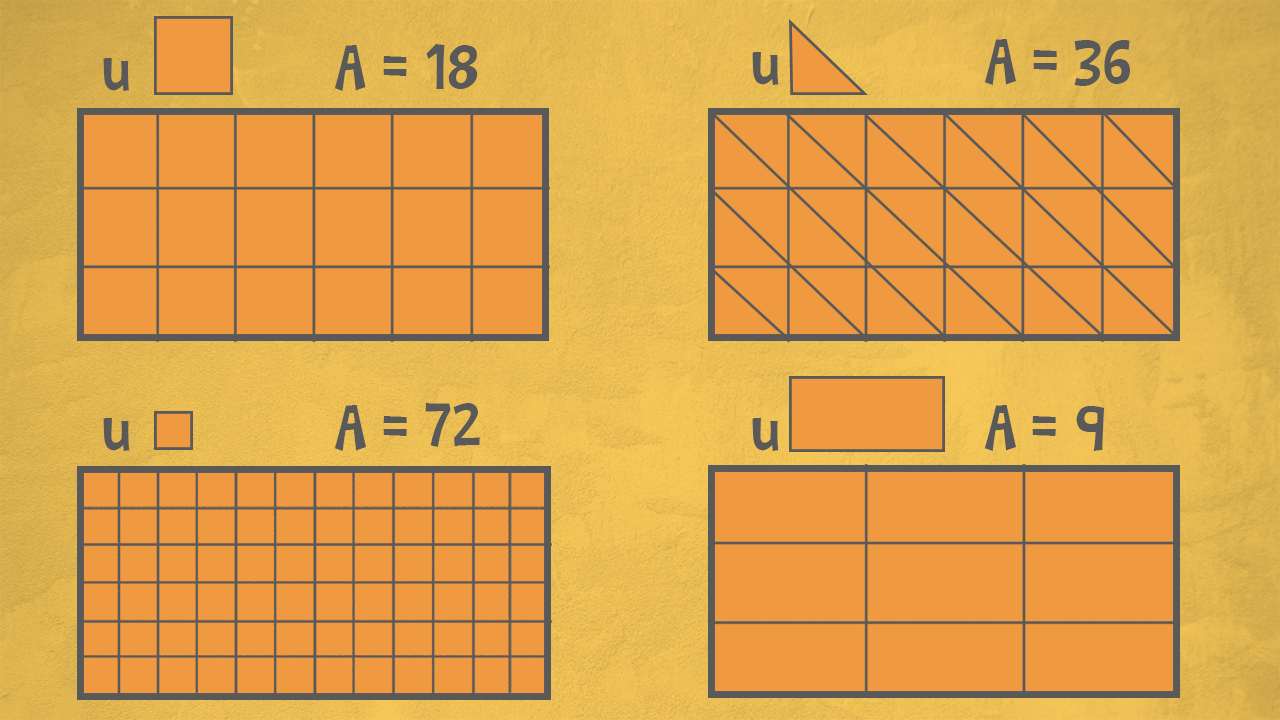
Per trovare l’area di un poligono, dobbiamo fare attenzione e utilizzare l’unità di misura più adatta.
Due figure che hanno la stessa area sono equiestese o equivalenti.
A seconda dell’unità di misura che scegliamo, otterremo delle misure diverse! Osserva le immagini: nei tre casi abbiamo scelto di misurare la superficie del poligono usando forme più o meno grandi, disposte in modi diversi. Otteniamo sempre un risultato diverso!
Come si calcola l’area dei poligoni regolari
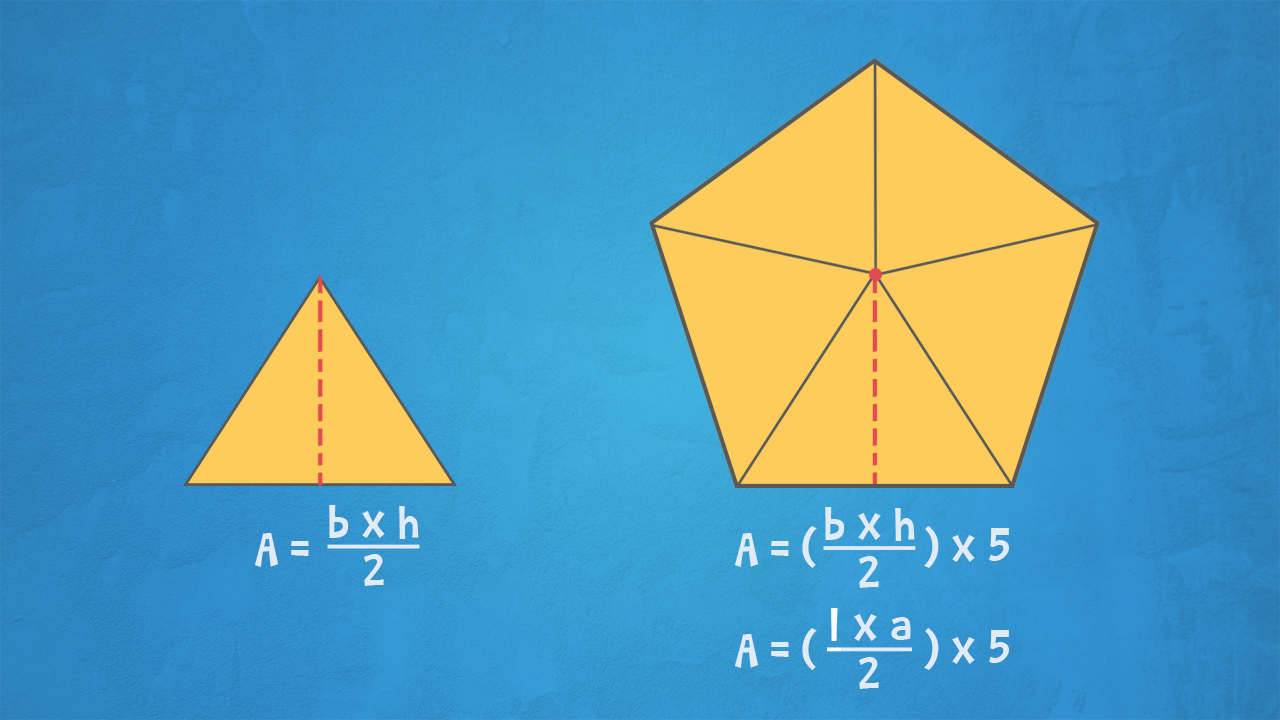
L’area dei poligoni regolari è data dalla somma delle aree dei triangolini che riusciamo a disegnare all’interno di ciascun poligono regolare.
Per trovare l’area di un triangolo dobbiamo moltiplicare la base per l’altezza e poi dividere per 2.
Ciascun triangolino in cui abbiamo suddiviso il poligono regolare ha come base il lato del poligono (l) e come altezza l’apotema (a). Dovremo moltiplicare questa quantità per il numero di triangolini ricavati in ciascun poligono, cioè per il numero di lati (n) del poligono regolare di cui stiamo calcoando l’area.
A = [(l x a) : 2] x n
Scheda attività – perimetri e aree

Capito come funzionano perimetri e aree? Ecco qualche attività per esserne più sicuri.
Iniziamo con una scheda. Osservate le figure realizzate sulla griglia a quadretti: non c’è bisogno di formule o altro, basta contare i quadretti che formano la linea di contorno per il perimetro e i quadretti che formano la superficie interna per l’area. Sfidate i ragazzi a realizzare altre immagini a quadretti: quale sarà la figura con l’area più grande che riusciamo a disegnare su quel foglio?
Passiamo a qualche attività più di movimento: qual è il vostro perimetro? Potete fare questa attività in palestra: un bambino si corica per terra e un altro, utilizzando dei mattoncini di legno (o delle matite, delle bottigliette di plastica… insomma degli oggetti che siano tutti uguali tra loro), calcola qual è il perimetro del bambino per terra. È un’attività di concentrazione per entrambi: chi è coricato deve mantenere la posizione finché l’altro non è riuscito a completare il perimetro e contare tutte le unità che ha utilizzato. Annotate tutti i perimetri in una tabella e confrontateli!
Torniamo in classe: avete un pavimento con piastrelle quadrate? Niente di più utile! Con un po’ di scotch di carta, i bambini possono “disegnare" delle figure nella griglia delle piastrelle e poi confrontare le loro aree contando i quadretti.
Un’ultima attività divertente: calcola il perimetro e l’area del tuo nome. Su un foglio a quadretti i bambini devono disegnare il loro nome, seguendo i quadretti: completato il disegno, possono calcolare perimetro e area. Raccogliete i dati in una tabella e confrontateli: sarà interessante collegare argomenti di statistica.
