Cosa sono i segmenti nel piano cartesiano

Il piano cartesiano è uno strumento fondamentale nella matematica che permette di rappresentare e analizzare relazioni geometriche e algebriche in modo visivo. Un elemento chiave in questo contesto è il segmento, una parte di una retta delimitata da due punti.

Questa struttura semplice ma essenziale è cruciale per comprendere concetti come la distanza e la posizione nello spazio. Scopriamo insieme cos’è il segmento e qual è la sua funzione nel piano cartesiano!

• Cosa sono i segmenti in geometria
• I segmenti nel piano cartesiano
• I segmenti costituiscono i poligoni nel piano cartesiano

Cosa sono i segmenti in geometria

Nel piano cartesiano, un segmento è una parte di una retta compresa tra due punti. Questi due punti, noti come estremi del segmento, definiscono la sua lunghezza e posizione nel piano. Il piano cartesiano stesso è un sistema di coordinate che utilizza due assi perpendicolari (di solito chiamati asse x e asse y) per definire la posizione di punti, linee e altre forme geometriche.

Quando parliamo di segmenti nel piano cartesiano, ci riferiamo spesso alla loro rappresentazione tramite coordinate. Ogni estremo del segmento ha una coppia di coordinate (x, y) che ne definisce la posizione. Ad esempio, un segmento potrebbe avere un estremo nel punto (x1, y1) e l’altro nel punto (x2, y2).

La lunghezza del segmento può essere calcolata usando il teorema di Pitagora, considerando la differenza tra le coordinate x e le coordinate y dei due punti. Questo è possibile perché i segmenti formati dalla differenza delle coordinate x e y sono i cateti di un triangolo rettangolo, con il segmento stesso come ipotenusa.

I segmenti nel piano cartesiano sono fondamentali nella geometria analitica, dove vengono utilizzati per studiare le proprietà di figure più complesse, come triangoli, quadrilateri e forme poligonali. Essi permettono di applicare metodi algebrici per risolvere problemi geometrici, collegando così due importanti aree della matematica: l’algebra e la geometria.

I segmenti nel piano cartesiano

Segmenti orizzontali e verticali

Teorema Pitagora sul piano cartesiano

Esercizio svolto: distanza tra due punti

Il piano cartesiano è un normalissimo piano, solo che ha un sistema di riferimento tale per cui riusciamo a individuare la posizione dei punti e delle figure disegnate sul piano.

Abbiamo già parlato delle coordinate dei punti: sono due numeri.

• Il primo indica la posizione lungo l’asse £$ x $£ (o asse delle ascisse)
• il secondo indica la posizione lungo l’asse £$ y $£ (o asse delle ordinate).

Congiungendo due punti qualsiasi £$ A(x_A; y_A) $£ e £$ B(x_B; y_B) $£ sul piano cartesiano troviamo un segmento £$ AB $£. Come facciamo a calcolare la lunghezza di un segmento nel piano cartesiano?

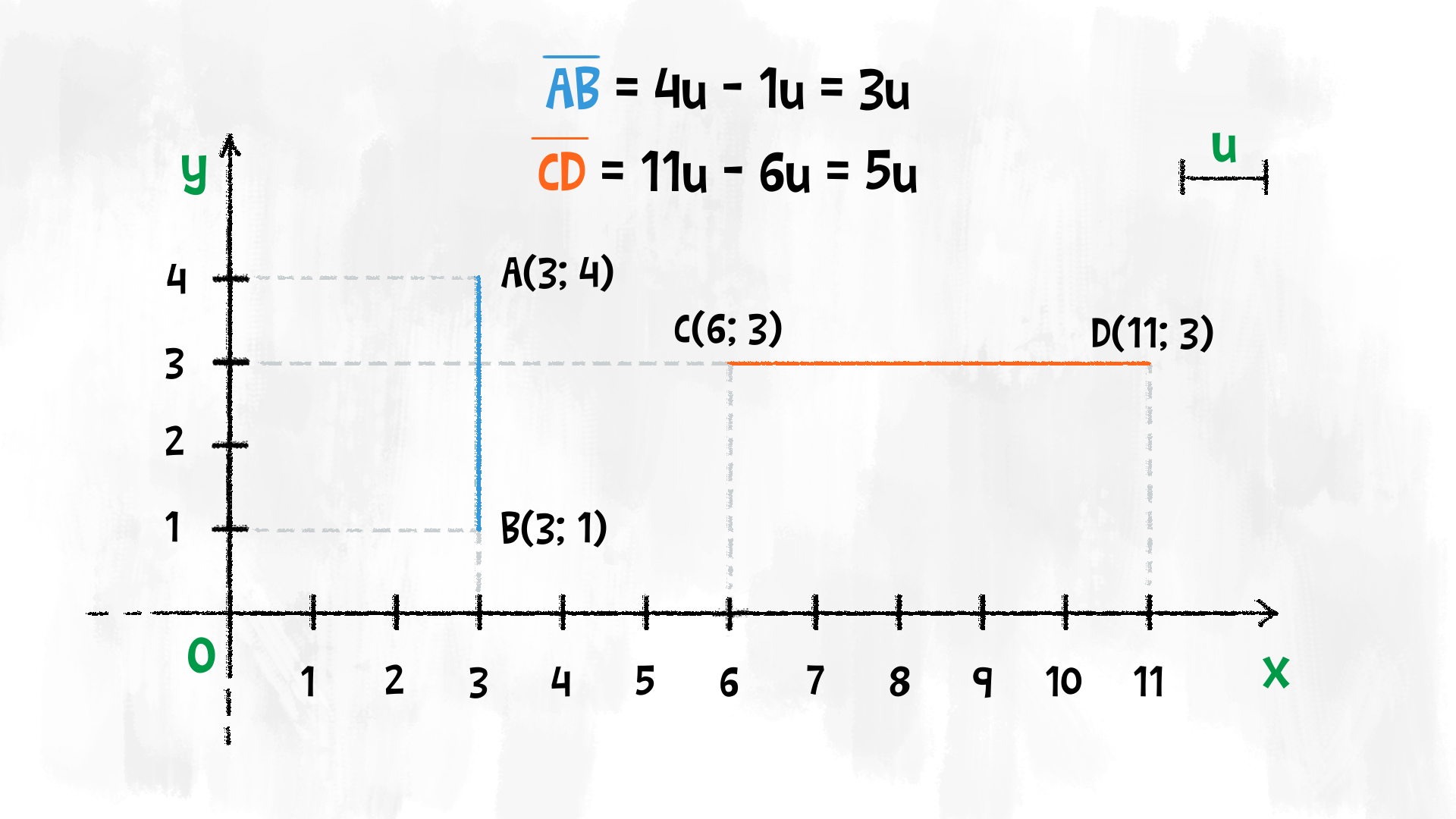
• Se i due estremi hanno la stessa ascissa, si tratta di un segmento verticale: possiamo calcolare la sua lunghezza con una semplice differenza tra le ordinate. Se £$ y_B > y_A $£, troviamo che il segmento ha lunghezza £$ \overline{AB} = y_B – y_A $£, altrimenti viceversa.
• Se i due estremi hanno la stessa ordinata, si tratta di un segmento orizzontale: possiamo calcolare la sua lunghezza con una semplice differenza tra le ascisse. Se £$ x_B > x_A $£, troviamo che il segmento ha lunghezza £$ \overline{AB} = x_B – x_A $£, altrimenti viceversa.

E come facciamo se siamo di fronte ad un segmento che non è né verticale né orizzontale? Qui viene in nostro aiuto il teorema di Pitagora.

Possiamo costruire sul piano cartesiano un triangolo rettangolo avente come ipotenusa il segmento £$ AB $£. Quanto misurano i due cateti? Costruiamo il cateto orizzontale che misura £$ x_B – x_A $£ e il cateto verticale che misura £$ y_B – y_A $£. Applichiamo quindi il teorema di Pitagora e troviamo la lunghezza del segmento £$ AB $£:

$$ \overline{AB} = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} $$

I segmenti costituiscono i poligoni nel piano cartesiano

Aree nel piano cartesiano

Esercizio svolto

Sul piano cartesiano possiamo disegnare punti, segmenti e anche poligoni: basta congiungere più segmenti a formare una linea spezzata chiusa.

Possiamo calcolare il perimetro e l’area di un poligono sul piano cartesiano:

• Per trovare il perimetro, dobbiamo calcolare le lunghezze di tutti i segmenti e sommarle.
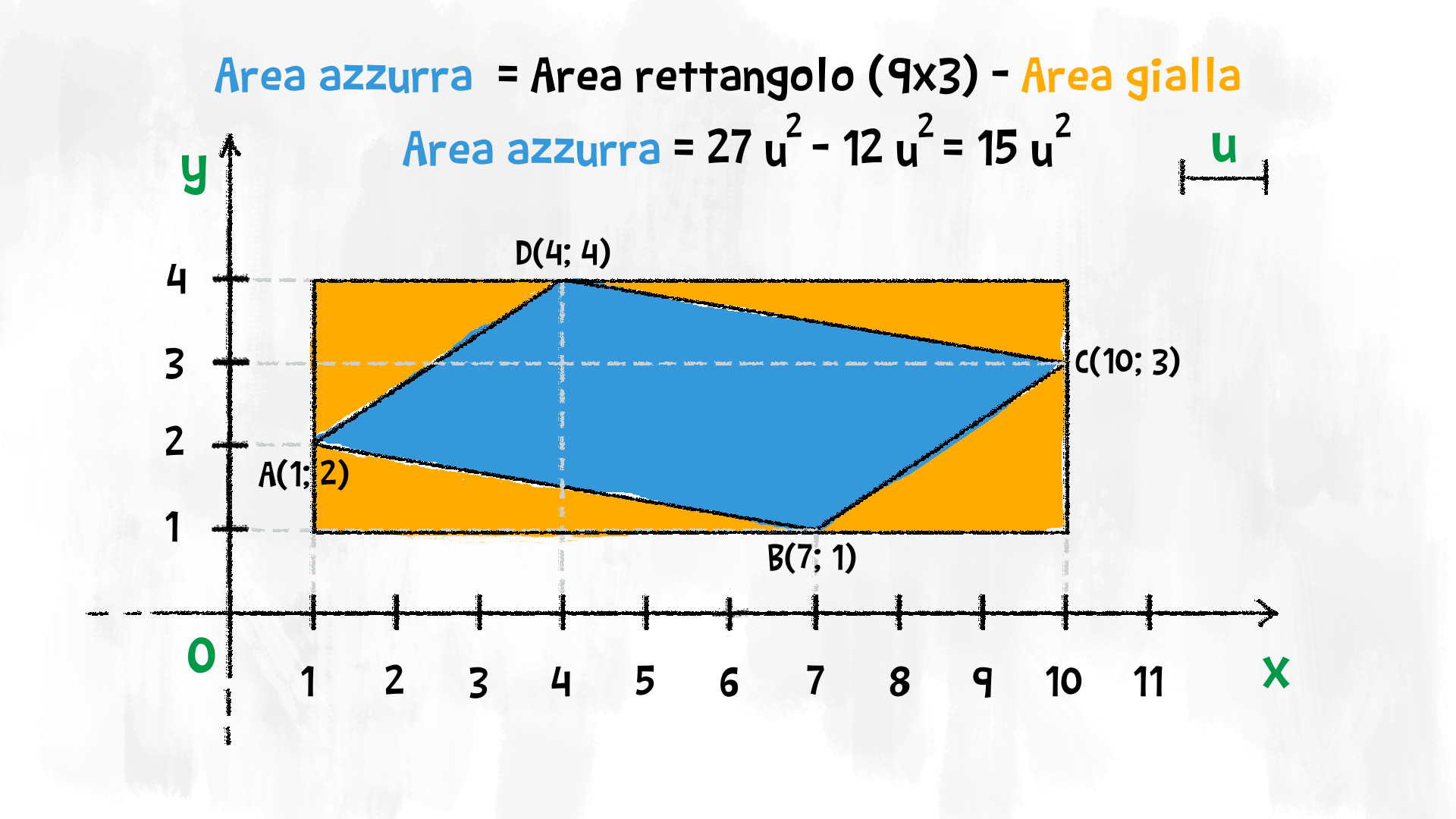
• Per calcolare l’area, possiamo aiutarci costruendo sul piano cartesiano delle figure di cui conosciamo l’area, e poi trovare le aree della figura che stiamo cercando.

Abbiamo imparato che i segmenti di cui è più facile trovare la lunghezza sono quelli orizzontali e verticali. Per calcolare l’area di una figura strana sul piano cartesiano, troviamo il rettangolo che la racchiude e arriviamo all’area finale sottraendo le aree dei triangoli o delle altre figure che riusciamo a riconoscere.