
Prova di Matematica Maturità 2025: problemi, quesiti e soluzioni
Tutte le soluzioni ai quesiti e ai problemi proposti nella seconda prova scritta di matematica all'esame di Maturità 2025 per il liceo scientifico
Questa mattina, alle 8.30, è iniziata la seconda prova della Maturità 2025. I maturandi del liceo scientifico si sono cimentati nella prova di matematica, composta da due problemi e otto quesiti. Ogni studente ha dovuto scegliere un problema e quattro quesiti da svolgere in sei ore. In questo articolo trovate le soluzioni degli esercizi proposti dal ministero dell’Istruzione e del Merito.
Le soluzioni dei problemi della prova di matematica alla Maturità 2025
Anche quest’anno, la traccia della prova di matematica dell’esame di Stato 2025 per il liceo scientifico è composta da due problemi e otto quesiti. Vediamo insieme la risoluzione dei problemi, come riportata da Sky Tg24.
- Problema 1

Prima parte del problema numero 1 della prova di matematica alla Maturità 2025
Al punto a), il compito presenta una circonferenza con raggio parametrico e una funzione contenente un parametro. Agli studenti viene richiesto di verificare la continuità e la non derivabilità della funzione nell’origine. Dopo di che si devono determinare i valori dei parametri in modo che il grafico della funzione e della circonferenza definiscano un settore circolare con area e contorno predeterminati.
Il punto b) è uno studio di funzione caratterizzato da una radice pari standard. Si chiede di verificare che il grafico della funzione coincida con la semicirconferenza nel semipiano con ordinata positiva. Dopo di che, si deve spiegare perché la funzione non è invertibile e trovare l’intervallo massimo di invertibilità.

Seconda parte del problema numero 1 della prova di matematica alla Maturità 2025
Passando al punto c), il problema richiede di individuare le coordinate di un punto specifico sul grafico della funzione, con l’obiettivo di massimizzare l’area del quadrilatero formato dalle sue proiezioni. Questo implica l’espressione dell’area in funzione di una delle coordinate, sfruttando l’espressione analitica della funzione g(x), per poi determinarne il valore massimo. Successivamente, si deve verificare che il quadrilatero così ottenuto sia un quadrato e che il suo perimetro raggiunga anch’esso il valore massimo.
Infine, al punto d), la traccia sposta l’attenzione su uno studio di funzione integrale. Il compito include anche la richiesta di determinare l’equazione della retta tangente nel punto di flesso della funzione.
- Problema 2
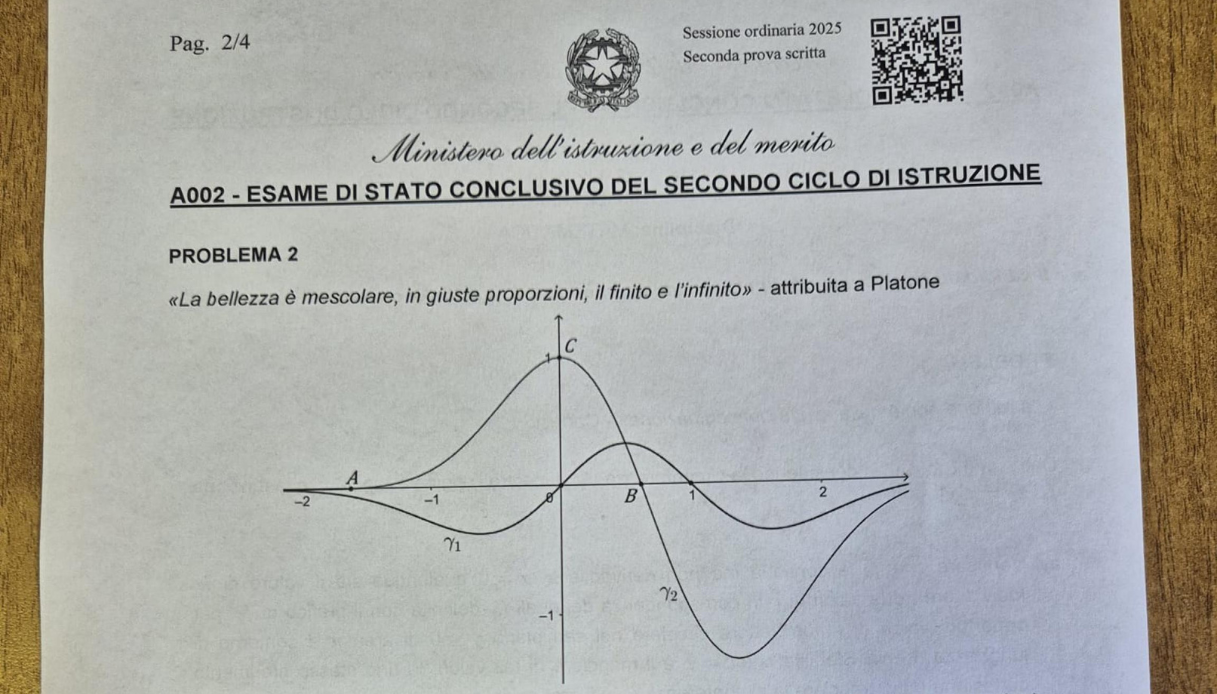
I grafici del problema numero 2 della prova di matematica alla Maturità 2025
Il problema 2 si apre con il punto a) che si concentra sull’identificazione dell’equazione di due funzioni, fornite solo tramite il loro grafico e alcune informazioni aggiuntive. Un aspetto interessante è la possibilità di impiegare i dati dei punti successivi b) e c) per una verifica incrociata dei risultati ottenuti in questa prima fase. Per risoluzione di questa sezione può essere utile conoscere le proprietà del rapporto aureo.

Il problema numero 2 della prova di matematica alla Maturità 2025
Il punto b) prosegue chiedendo lo studio di una delle due funzioni precedentemente determinate, utilizzando i metodi standard dell’analisi e trovandone l’immagine. Successivamente, viene posta la questione del numero di intersezioni tra la funzione (che si rivela essere un polinomio moltiplicato per una funzione esponenziale) e una retta orizzontale al variare dell’altezza di quest’ultima.
Nel punto c), la traccia si sposta sull’altra funzione, ponendo diverse domande e richiedendo la dimostrazione di alcune proprietà geometriche dei segmenti ottenuti. Questi segmenti sono ottenuti collegando zeri, punti di intersezione, massimi e minimi delle curve. La risoluzione di questa parte è interamente affidata a nozioni di calcolo differenziale e geometria nel piano, come l’equazione della retta passante per due punti.
Infine, il punto d) verte sul calcolo di aree comprese tra curve e assi. Per risolverlo è necessario risolvere degli integrali definiti.
Le soluzioni dei quesiti della prova di matematica alla Maturità 2025
Oltre ai problemi, gli studenti dello scientifico si sono trovati davanti anche a otto quesiti, tra i quali ne hanno dovuti scegliere quattro. Vediamo insieme la risoluzione dei quesiti, come riportato da Sky Tg24.

I primi tre quesiti della prova di matematica alla Maturità 2025
- Quesito 1
Il primo quesito invita i candidati a dimostrare la congruenza tra due specifici segmenti. La sua risoluzione richiede l’applicazione di diverse nozioni, spaziando dall’utilizzo delle coordinate alla geometria euclidea, fino alle simmetrie.
- Quesito 2
Il secondo quesito chiede di stabilire la posizione reciproca tra una sfera e un piano π al variare di un parametro reale. Per risolverlo, si deve confrontare la distanza tra il centro della sfera e il piano con il raggio della sfera, controllando se sono secanti, tangenti o se la sfera è esterna. Infine, bisogna trovare il valore del parametro affinché il piano risulti diviso in parti uguali, calcolo che implica l’analisi delle aree.
- Quesito 3
Il terzo quesito riguarda lo studio di una funzione definita a tratti con dominio [−1,2]. Si chiede di tracciare il grafico della funzione e di analizzare la sua continuità e derivabilità all’interno del dominio di definizione. La funzione è composta da due parti: una parabola e una funzione trigonometrica (in particolare una tangente).

I quesiti 4, 5 e 6 della prova di matematica alla Maturità 2025
- Quesito 4
Il quarto quesito verte sulla determinazione dell’equazione della retta normale a una curva in un punto specifico. Per la sua risoluzione è necessario conoscere il calcolo differenziale, con particolare riferimento alle regole di derivazione di funzioni trigonometriche e di un prodotto di funzioni, oltre a nozioni di geometria relative alle curve trigonometriche e alle rette.
- Quesito 5
Il quinto quesito si focalizza sulla condizione di tangenza tra curve, rendendo indispensabile una solida conoscenza delle proprietà delle funzioni logaritmiche ed esponenziali e nelle derivate delle funzioni. Sono richieste anche competenze algebriche per la risoluzione dei sistemi di equazioni.
- Quesito 6
Il sesto quesito chiede di costruire una funzione polinomiale che soddisfi due condizioni specifiche: tangenza con una retta data in un determinato punto e il raggiungimento di un risultato preciso dall’integrale definito di tale funzione.

Il quesito numero 7 della prova di matematica alla Maturità 2025
- Quesito 7
Il quesito numero 7 presenta un problema standard di calcolo delle probabilità associato al lancio di dadi. L’unica peculiarità è la presenza di dadi a quattro facce.

Il quesito numero 8 della prova di matematica alla Maturità 2025 e la citazione di Hilbert
- Quesito 8
Il quesito 8, infine, è incentrato sul calcolo combinatorio e richiede il calcolo delle permutazioni tenendo conto delle ripetizioni.
