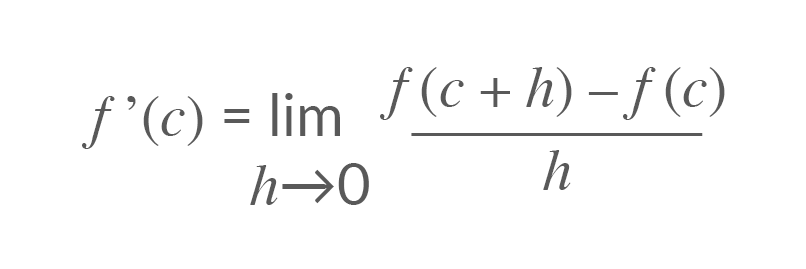Le derivate: definizione, esempi ed esercizi
Le derivate sono uno dei concetti fondamentali in matematica, in particolare nel campo del calcolo differenziale. Rappresentano uno strumento potente per analizzare il modo in cui una funzione cambia al variare del suo input. In termini più semplici, la derivata di una funzione in un punto fornisce il tasso di variazione istantaneo della funzione in quel punto, o equivalentemente, la pendenza della tangente alla curva della funzione in quel punto.
Il calcolo delle derivate inizia con funzioni semplici e si estende a funzioni più complesse attraverso l’uso di regole e tecniche specifiche, come la regola del prodotto, la regola del quoziente e la regola della catena. Queste tecniche permettono di derivare funzioni complesse a partire dalle derivate di funzioni più semplici.
Vediamo insieme quali sono le loro caratteristiche.
- Cosa sono e a cosa servono le derivate
- Chi ha scoperto le derivate
- Qual è il significato geometrico di derivata
- Derivata come limite del rapporto incrementale
Cosa sono e a cosa servono le derivate
Una funzione può essere crescente, decrescente o stazionaria.
La derivata ci dice come cambia una funzione in un intervallo o in un punto, quindi ci permette anche di stabilire quali sono i suoi punti di massimo e di minimo.
Se analizziamo la variazione della funzione in un solo punto, allora la derivata è il coefficiente angolare della retta tangente al grafico della funzione in quel punto.
Chi ha scoperto le derivate
Newton fu il primo a introdurre il concetto di derivata, intorno al 1669, per risolvere problemi come quello del calcolo della velocità istantanea in fisica, ma non pubblicò mai nulla. Liebniz invece fu il primo ad affrontare il calcolo delle derivate con un approccio geometrico.
Intorno al 1665 pubblicò le sue scoperte che, essendo più facili da capire, si diffusero velocemente in tutta Europa, prima di quelle di Newton, che non prese bene la notizia e accusò Liebniz di aver copiato le sue scoperte!
Liebniz sosteneva fermamente di essere arrivato alle sue conclusioni indipendentemente da quelle di Newton.
Per dimostrarlo, chiese alla Royal Society di Londra (Accademia Nazionale Inglese delle Scienze) di convocare una commissione d’inchiesta per risolvere la questione.
Nel 1712, Liebniz fu ufficialmente accusato di plagio. Povero Liebniz! Non era stato molto fortunato perché Newton, proprio quell’anno, aveva dalla sua il fatto di essere il presidente della Royal Society!
Qual è il significato geometrico di derivata
La derivata prima di una funzione in un punto è l’£$m$£, cioè il coefficiente angolare della retta tangente la funzione in quel punto.
Che cosa era il coefficiente angolare? Ricordiamo l’equazione esplicita della retta: £$ y=mx+q$£. £$ m $£ è il coefficiente angolare, cioè la pendenza della retta rispetto all’asse delle £$x$£.
Puoi calcolarlo se conosci due punti £$A(x_A,y_A)$£ e £$ B(x_B; y_B)$£ della retta come il seguente rapporto: £$ m=\frac{y_B-y_A}{x_B-x_A}$£.
Sappiamo che non tutte le rette possono essere scritte nella forma esplicita. Le rette parallele all’asse delle £$y$£, cioè quelle verticali, non sono delle funzioni, quindi non possono essere scritte nella forma £$y=mx+q$£.
Ciò significa che la loro £$ m $£ non esiste quindi, non esiste nemmeno la derivata!
Derivata come limite del rapporto incrementale
Prendi una funzione £$f$£ definita in £$ [a,b] $£ e considera £$ c \in [a,b] $£ e £$P (c; f(c))$£ un punto qualsiasi di questa funzione.
La derivata prima della funzione £$f$£ in quel punto è il limite, se esiste, del rapporto incrementale di £$f$£ relativo a £$c$£, per £$h$£ che tende a zero:
