Punti di discontinuità e asintoti di una funzione
Impara cosa sono e come classificare i punti di discontinuità: prima, seconda e terza specie. Scopri come trovare l’equazione di un asintoto verticale, orizzontale ed obliquo!
Cos’è un asintoto e quali sono i punti di discontinuità? Qual è la definizione di continuità e discontinuità tramite i limiti? Impara come riconoscere le discontinuità di prima, seconda e terza specie. Impara in quali punti e come si cercano gli asintoti. Vediamo quali limiti risolvere per calcolare gli asintoti verticali, orizzontali ed obliqui.
In questa lezione imparerai:
- Punti di discontinuità: definizione di funzione continua, di discontinuità in un punto e di discontinuità di prima, seconda e terza specie
- Asintoti orizzontali e verticali: dove cercare, come calcolare e qual è l’equazione degli asintoti verticali ed orizzontali
- Asintoti obliqui: quando esiste un probabile asintoto obliquo, quando è definito e qual è la sua equazione
- Cosa sono i punti di discontinuità
- Asintoti orizzontali e verticali
- Asintoti obliqui
- Esercizi su discontinuità e asintoti
- Sfida sulle discontinuità
Cosa sono i punti di discontinuità
Una funzione è continua in un intervallo £$[a,b]$£ se per ogni punto £$x_0$£ dell’intervallo è sempre verificato che £$\lim\limits_{x \to x_0} f(x)=f(x_0)$£.
Se una funzione non è continua in un punto £$x_0$£, £$x_0$£ è punto di discontinuità. Esistono 3 tipi di discontinuità:
- discontinuità di prima specie ("a salto"): esistono finiti i limiti destro e sinistro della funzione, ma hanno due valori diversi. £$\lim\limits_{x \to x_0^-}f(x)=l_1 \ne \lim\limits_{x \to x_0^+} f(x)=l_2$£
- discontinuità di seconda specie: almeno uno fra il limite destro (£$\lim\limits_{x \to x_0^+} f(x)$£) e sinistro (£$\lim\limits_{x \to x_0^-}f(x)$£) della funzione è infinito o non esiste
- discontinuità di terza specie ("eliminabile"): esiste finito il limite £$l$£ della funzione nel punto £$x_0$£: £$\lim\limits_{x \to x_0} f(x)=l$£, ma la funzione o non è definita in quel punto, oppure è definita ma non è continua, ossia £$f(x_0) \ne l$£.
Asintoti orizzontali e verticali
L’asintoto di una curva è una retta che si avvicina sempre di più alla funzione senza però toccarla mai: la distanza tra la retta e la curva tende a zero.
Come trovare e dove cercare un asintoto?
Cerchiamo gli asintoti nei punti in cui la funzione non è definita, oppure all’infinito. Per trovare gli asintoti della funzione £$f(x)$£, devi quindi calcolare dei limiti. Avrai:
- un asintoto verticale se £$\lim\limits_{x \to x_0} f(x)= \infty$£. La retta £$x=x_0$£ è un asintoto verticale per la funzione £$f(x)$£
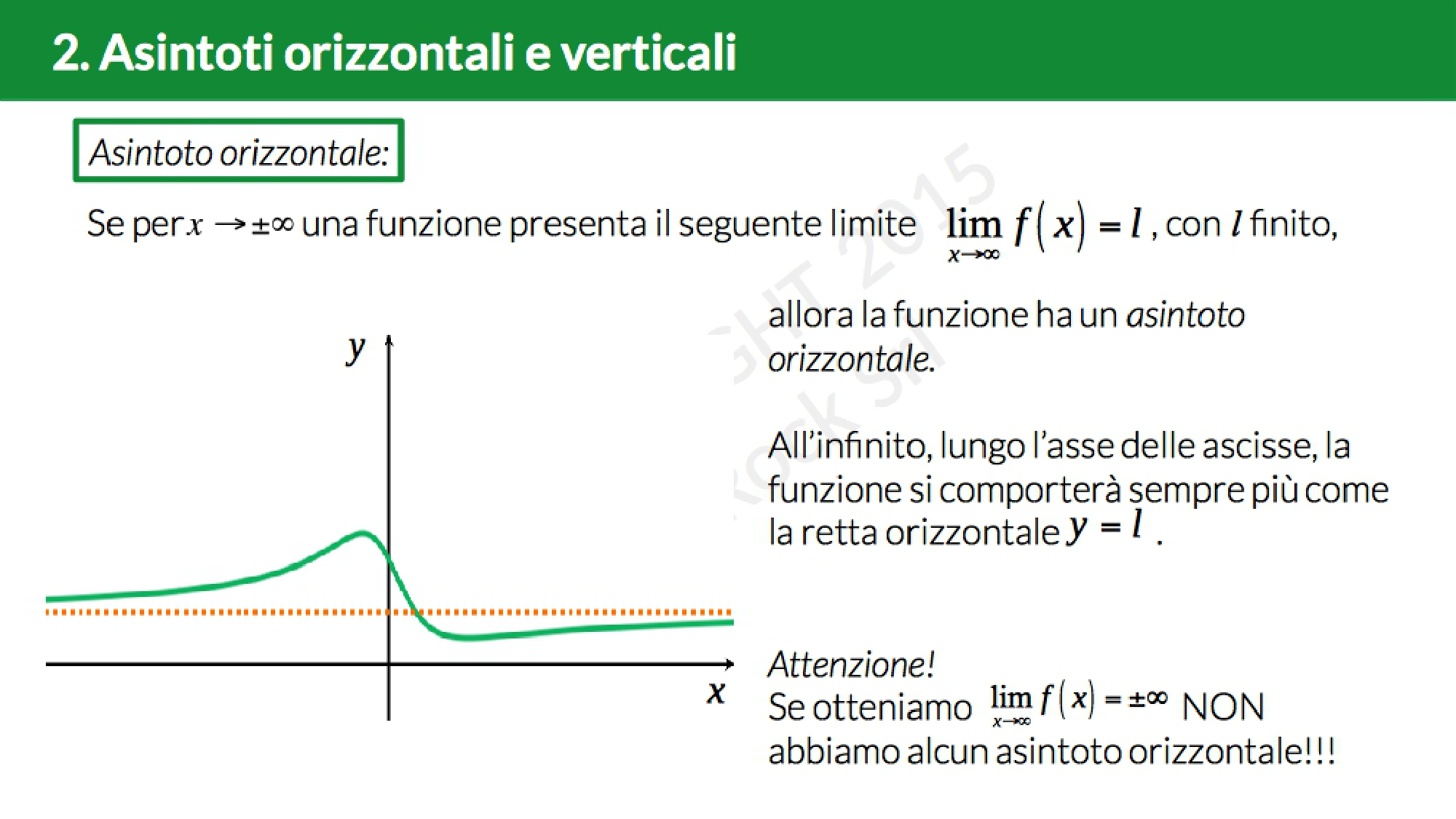
- un asintoto orizzontale se £$\lim\limits_{x \to \infty} f(x)=l$£, con £$l$£ finito. La retta £$y=l$£ è un asintoto orizzontale per la funzione £$f(x)$£.
Asintoti obliqui
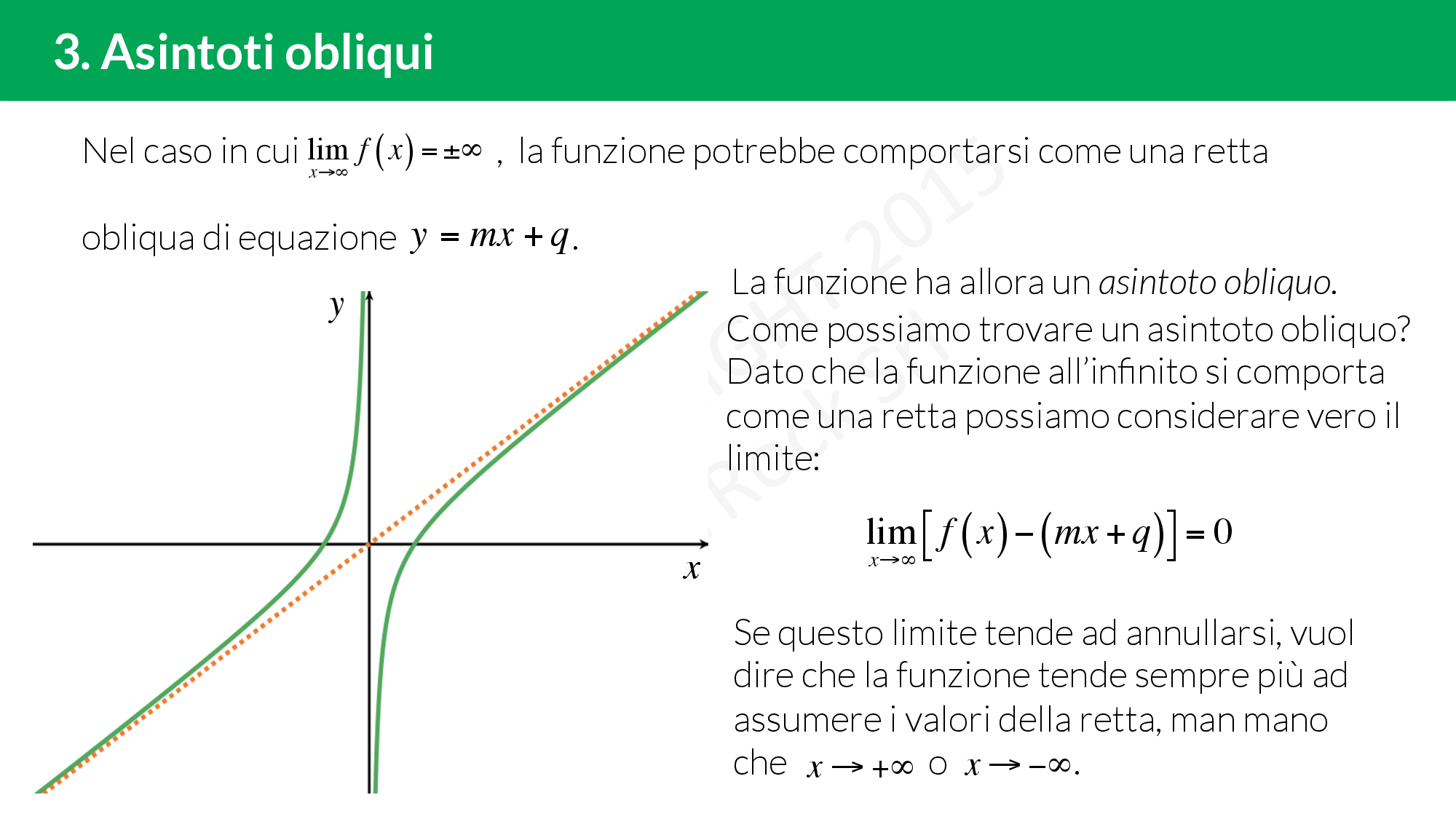
Se il limite all’infinito è ancora un valore infinito abbiamo invece un probabile asintoto obliquo: £$\lim\limits_{x \to \infty} f(x)=\pm \infty$£
Quando esiste davvero l’asintoto obliquo e come posso trovare la sua equazione?
- Se esiste finito e non nullo il limite £$\lim\limits_{x \to \infty} \frac{f(x)}{x}$£, allora questo è proprio il coefficiente angolare £$m$£ dell’asintoto obliquo: £$m=\lim\limits_{x \to \infty} \frac{f(x)}{x}$£.
- Se esiste l’£$m$£, puoi calcolare anche l’intercetta dell’asintoto obliquo £$q$£: £$q=\lim\limits_{x \to \infty} \left[ f(x)-mx \right]$£.
Esercizi su discontinuità e asintoti
Testo e soluzione:
Ora che sai cosa potrebbe "andare storto" nello studio di una funzione e nel calcolo dei limiti, perfeziona le tue conoscenze provando a risolvere questi esercizi sui punti di discontinuità e sul calcolo degli asintoti orizzontali, verticali e obliqui!
Sfida sulle discontinuità
Testo e soluzione:
Ormai devi sistemare il Wi-Fi di tutti! Ma è facile, visto che sei un mago dei limiti!
Riuscirai anche questa volta a far funzionare tutto? Prova a risolvere la sfida!