I limiti in matematica: definizione e calcolo
I limiti sono uno strumento essenziale per comprendere il comportamento delle funzioni e per affrontare problemi complessi in diversi ambiti della scienza e dell’ingegneria. Partiremo dalle basi, definendo cosa sono i limiti in matematica, come vengono formalmente definiti e come possono essere calcolati attraverso vari metodi.
Un limite, in termini semplici, descrive il valore a cui si avvicina una funzione man mano che l’input si avvicina a un certo punto. Questo concetto è fondamentale per analizzare il comportamento delle funzioni in punti specifici, specialmente in quei punti dove la funzione stessa potrebbe non essere definita.
Scopriamo insieme come fare, come possiamo definirli e come si calcolano!
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Cosa sono i limiti di una funzione
- Definizione di limite di una funzione
- Risultati possibili nel calcolo di un limite
- Esercizi da svolgere sul concetto di limite
Cosa sono i limiti di una funzione
Cos’è il limite di una funzione
A cosa servono i limiti
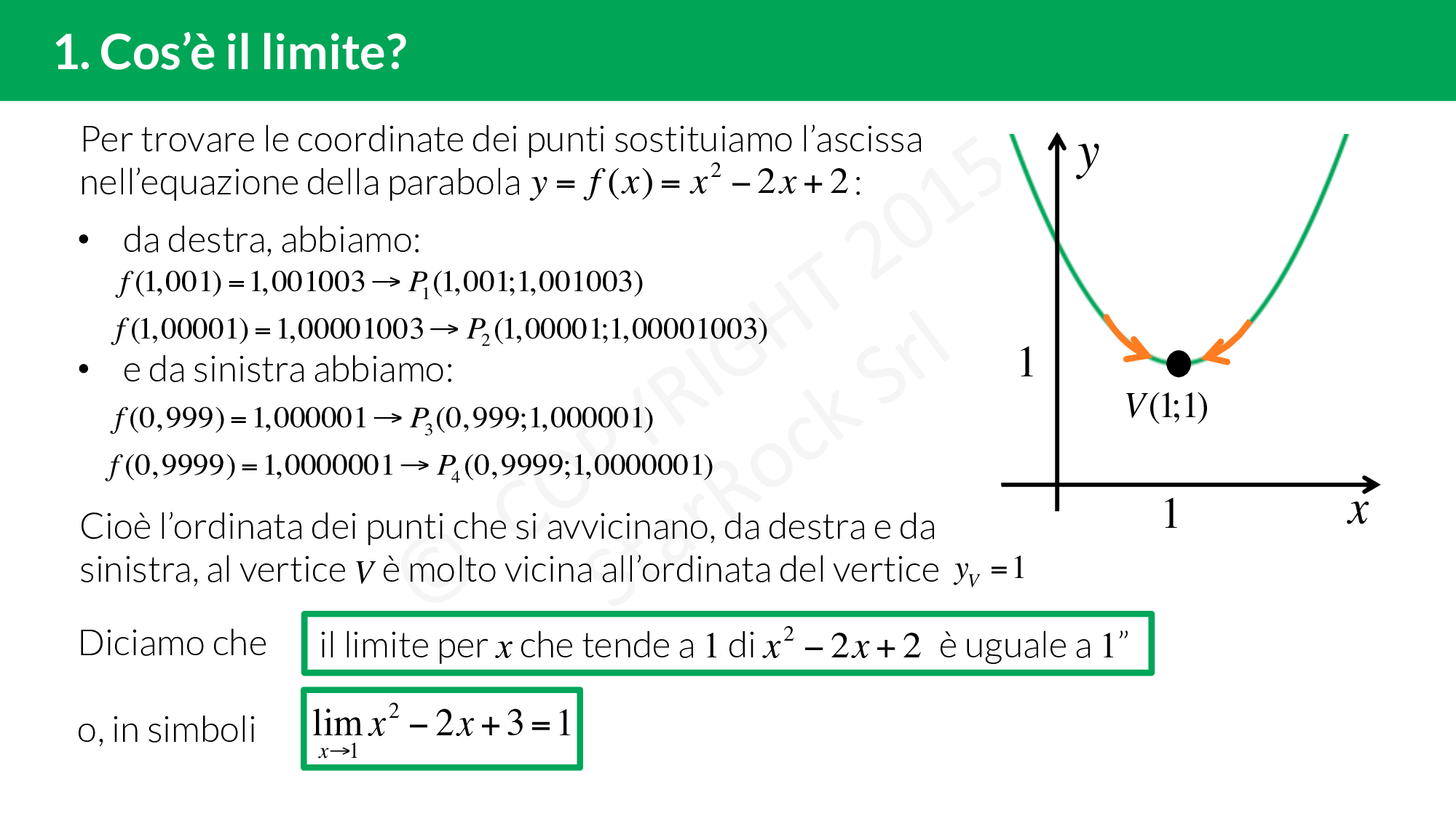
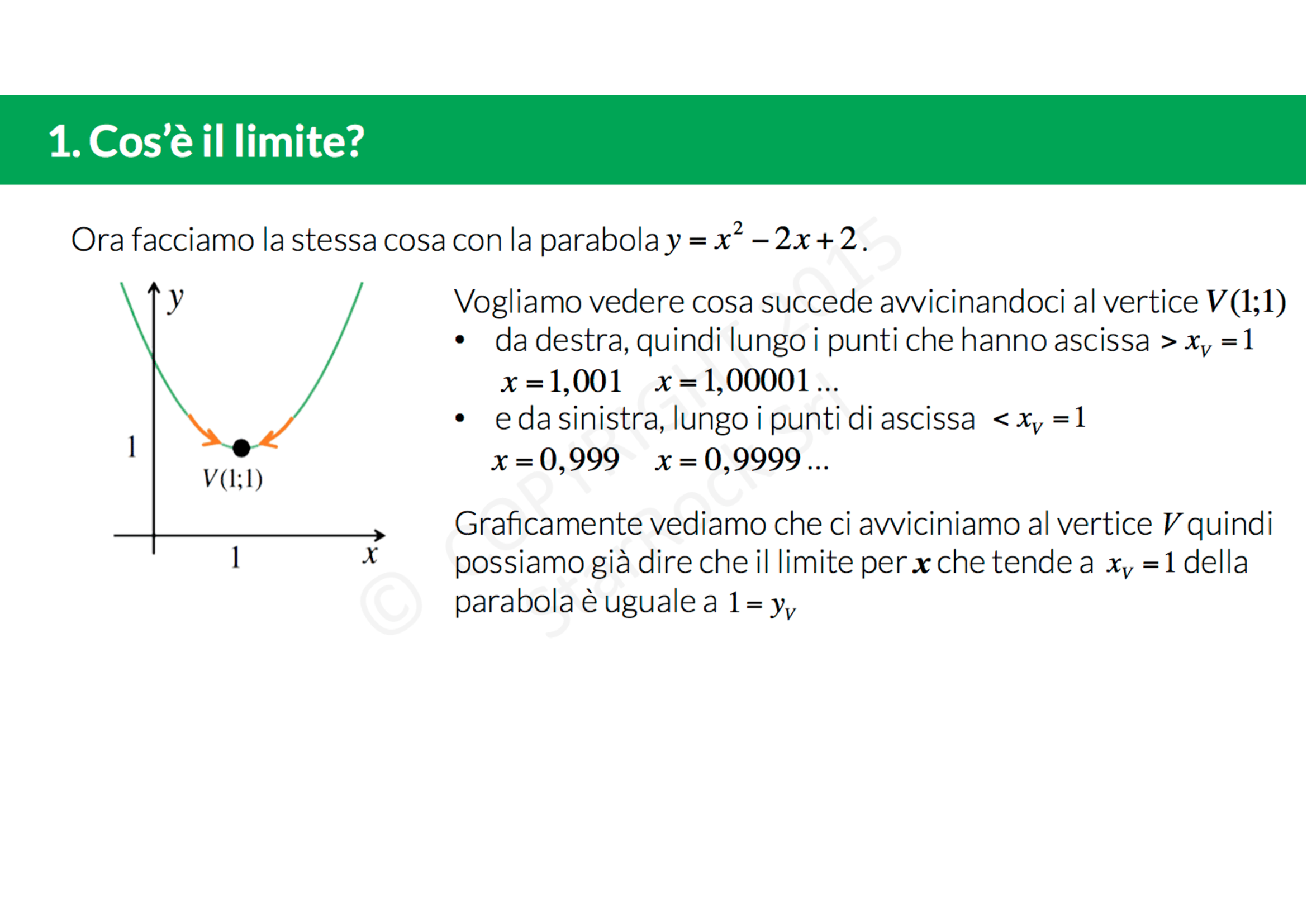
Il limite è uno strumento matematico che ci permette di capire come si comporta una funzione, cioè cosa succede alla £$y$£ nel suo grafico vicino a un punto con una certa ascissa £$x$£.
Si ma a cosa serve il calcolo di limiti? Il limite serve per capire come si comporta, quindi quali valori assume una funzione vicino a particolari punti del dominio o che non sono nel domino ma sono estremi del dominio. Quindi i limiti, in generale, sono legati al dominio della funzione.
Nelle funzioni "belle", cioè quelle in cui "va tutto bene", i limiti esistono e sono uguali al valore della funzione nel punto. Queste funzioni sono continue, cioè puoi disegnarle senza staccare mai la penna dal foglio.
Ci sono funzioni più "brutte", in cui accadono cose "strane" (buchi, salti, gradini…), queste funzioni sono discontinue e per sapere come si comportano vicino ai punti strani dobbiamo calcolarne il limite!
Definizione di limite di una funzione
Il concetto di limite è strettamente legato a quello di intorno di un punto. Ma che cos’è?
L’intorno di un punto è l’insieme dei punti che sono "vicini" a quel punto. Possiamo pensarlo come un intervallo (in £$\mathbb{R}$£) aperto contenente il punto.
Ad esempio, l’intervallo £$(0,3)$£ è un intorno di £$2$£ (ma anche di £$1$£) ma non è un intorno di [iol_placeholder type="formula" engine="katex" display="inline"/] perché non appartiene all’intervallo.
Quando calcoliamo il limite di una funzione in un punto, possono verificarsi tre casi:
- il limite esiste ed è un valore finito (cioè un numero);
- il limite esiste ma è infinito;
- il limite non esiste.
In base al questo possiamo definire il comportamento della funzione vicino al punto che ci interessa analizzare.
Risultati possibili nel calcolo di un limite
Il limite esiste finito
Il limite esiste infinito
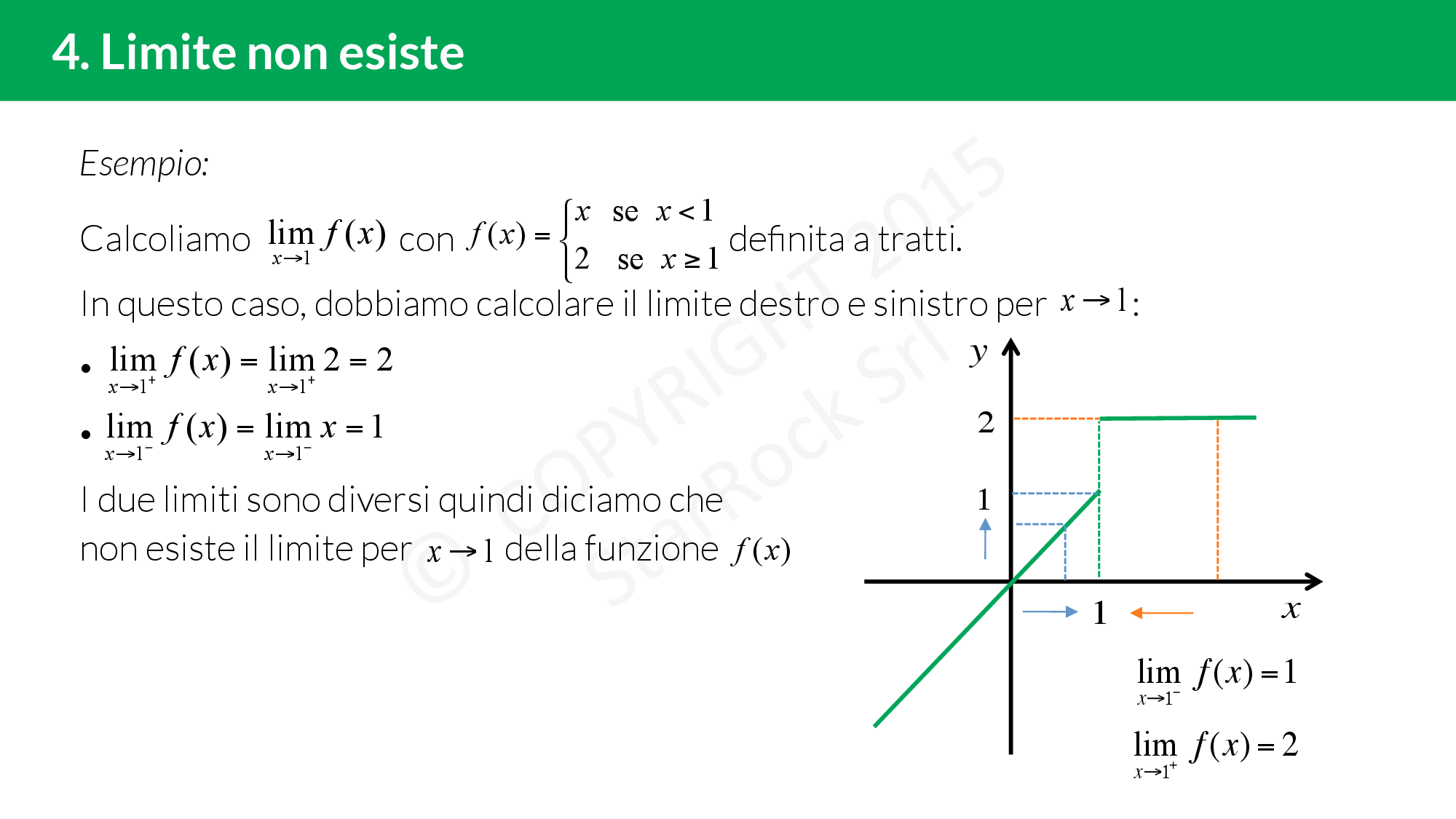
Il limite non esiste
Ogni volta che devi calcolare il limite di una funzione in un punto, possono verificarsi tre possibili risultati:
- il limite della funzione esiste ed è un numero;
- il limite esiste ma è uguale a infinito (£$+\infty$£ o £$-\infty$£);
- il limite non esiste.
Ma cosa significa che il limite esiste? Quando ci avviciniamo a un punto, possiamo farlo da valori più grandi (cioè da destra) o da valori più piccoli (o da sinistra). Se avvicinandosi da entrambi i lati, i valori che assume la funzione sono uguali, allora diciamo che il limite esiste. Altrimenti diciamo che il limite non esiste.
Facile no?
Esercizi da svolgere sul concetto di limite
Testo della sfida
Soluzione alla sfida
Eccoci pronti con la sfida sul concetto di limite! Questa volta devi risolvere il problema del segnale del tuo WiFi. Quanto distante puoi stare dal router?