La divisione: come si fa e quali sono le sue proprietà
La divisione rappresenta una delle operazioni fondamentali nella matematica e ci permette di ripartire una quantità in parti uguali. Immagina di avere un tesoro di monete d’oro e di volerlo dividere equamente tra tutti i tuoi amici: la divisione ti può aiutare in questo compito!
Nell’eseguire la divisione, abbiamo un numero chiamato dividendo che rappresenta la quantità totale da dividere. Il divisore, invece, indica in quante parti vogliamo suddividere il dividendo. La risposta a questa operazione si chiama quoziente.
Ma attenzione, a volte non possiamo dividere esattamente il dividendo per il divisore, e ciò che rimane si chiama resto. È come avere qualche moneta extra dopo aver diviso il tesoro con i tuoi amici.
La divisione è ovunque nella nostra vita quotidiana: dal dividere una pizza tra amici, al calcolare quante volte un numero si adatta in un altro. Così come la sottrazione, anche la divisione è un’operazione essenziale: scopri come farla e quali sono le sue proprietà!
Usa la mappa mentale per ripassare le proprietà delle divisioni. Tienila sempre sotto mano per non dimenticare niente. Con la pratica le divisioni non avranno più segreti per te!
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Obiettivi della divisione: distribuire e raggruppare
- I termini della divisione
- La divisione è una sottrazione ripetuta
- Divisioni fino al 100 e al 1000
- La proprietà invariantiva della divisione
- La proprietà distributiva della divisione
- Moltiplicazione e divisione per organizzare i compiti
- La mappa mentale della divisione
- Scheda attività - le divisioni
- Esercizi con le divisioni
Obiettivi della divisione: distribuire e raggruppare
Divisione per distribuire

Divisione per raggruppare

Abbiamo imparato che la divisione serve a distribuire e raggruppare.
Oscar deve mettere le sue 14 mosche in due gabbie, in modo che ce ne siano tante uguali in ciascuna gabbia. Quante ne metterà in ciascuna gabbia?
Per rispondere dobbiamo fare una divisione: 14 : 2 = 7. Abbiamo distribuito le 14 mosche in 2 gabbie e abbiamo trovato che ce ne devono essere 7 in ciascuna gabbia.
Lisa ha 15 farfalle, ne mette 3 in ogni gabbietta. Di quante gabbiette avrà bisogno?
Anche in questo caso serve una divisione: 15 : 3 = 5. Lisa avrà bisogno di 5 gabbiette per le sue farfalle: le abbiamo così raggruppate in gruppetti da 3.
I termini della divisione
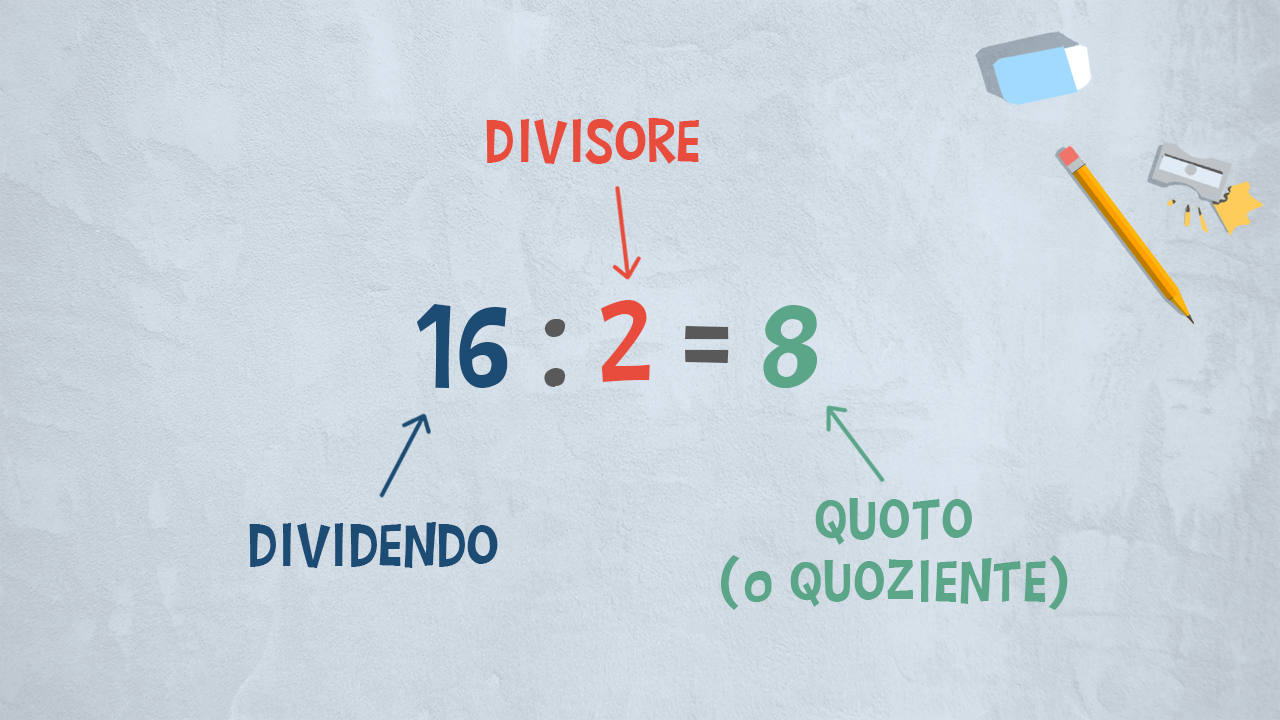
La divisione è l’operazione inversa della moltiplicazione. Ci aiuta quando dobbiamo spartire, suddividere in parti uguali, per non scontentare nessuno.
Il segno aritmetico che indica la divisione è £$ : $£ che leggiamo diviso.
Il primo termine della divisione si chiama dividendo, il secondo si chiama divisore. Possiamo scrivere, ad esempio, la divisione 15 : 5, dove il 15 è il dividendo e il 5 è il divisore.
Il risultato si chiama in due modi diversi:
- quoto se il dividendo è multiplo del divisore, quindi il risultato è un numero intero;
- quoziente se il dividendo non è un multiplo del divisore, quindi otteniamo un risultato con il resto.
Il quoto indica quante volte il divisore “sta" nel dividendo. Calcoliamo la divisione 16 : 2 = 8. Il quoto 8 ci dice che il 2 sta 8 volte nel 16. Infatti sappiamo che 2 x 8 = 16.
Se la divisione non è esatta, il risultato si chiama quoziente perché la divisione ha il resto.
La divisione è una sottrazione ripetuta
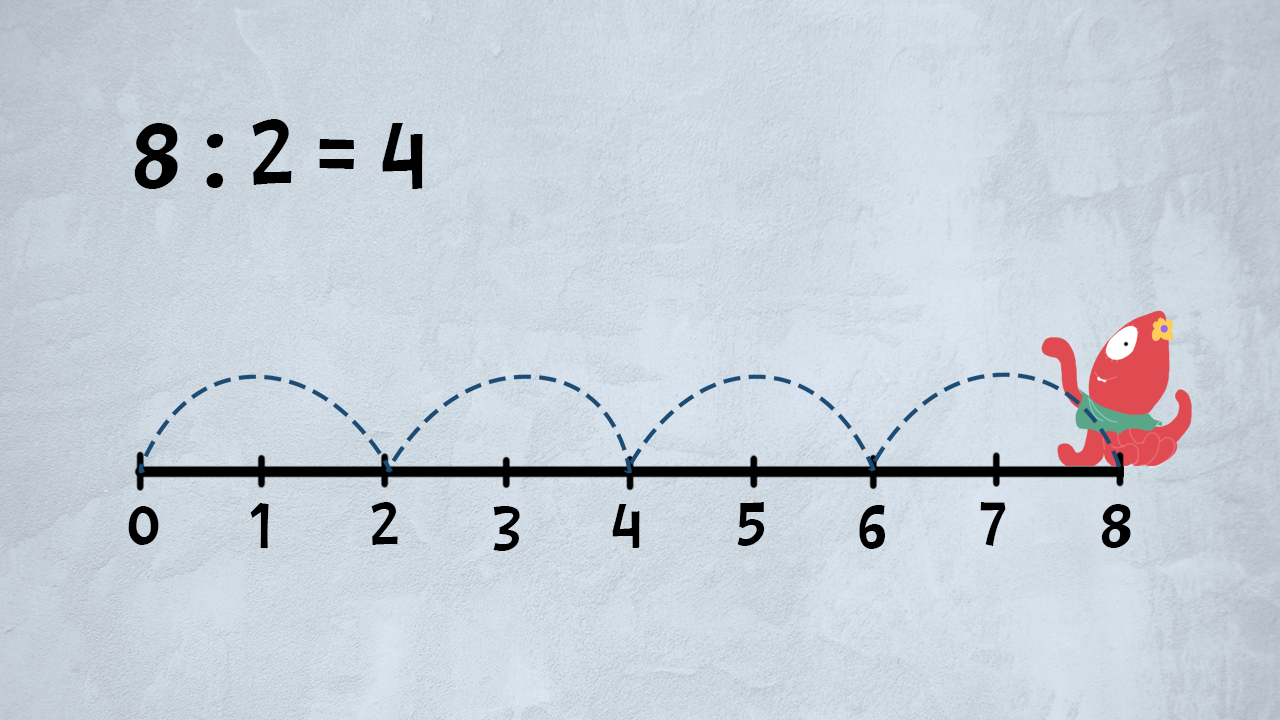
Visto che la sottrazione è l’operazione inversa dell’addizione e la divisione è l’operazione inversa della moltiplicazione, possiamo parlare di divisione come “sottrazione ripetuta".
Il risultato di una divisione, infatti, è uguale al numero di volte che riusciamo a sottrarre il divisore dal dividendo.
$$ 18 : 3 = ? $$
Proviamo a sottrarre il £$ 3 $£ al £$ 18 $£ e vediamo per quante volte riusciamo a farlo:
$$ 1) \ 18 – 3 = 15 \quad 2) \ 15 – 3 = 12 \quad 3) \ 12 – 3 = 9 \quad 4) \ 9 – 3 = 6 \quad 5) \ 6 – 3 = 3 \quad 6) \ 3 – 3 = 0 $$
Contiamo: quante volte siamo riusciti a sottrarre il £$ 3 $£ e arrivare a £$ 0 $£? Ci siamo riusciti per sei volte. Allora
$$ 18 : 3 = 6 $$
Se non riusciamo ad arrivare a £$ 0 $£, significa che siamo di fronte ad una divisione non esatta, cioè che ha il resto.
$$ 15 : 4 = ? $$
Sottraiamo il £$ 4 $£ al £$ 15 $£ e vediamo cosa riusciamo a trovare:
$$ 1) \ 15 – 4 = 11 \quad 2) \ 11 – 4 = 7 \quad 3) \ 7 – 4 = 3 $$
Non possiamo andare oltre. Siamo riusciti a sottrarre il £$ 4 $£ per tre volte, poi abbiamo avanzato £$ 3 $£. Quindi il risultato di questa divisione è:
$$ 15 : 4 = 3 \text{ con il resto di } 3 $$
Divisore uguale a 1

Se dividiamo un numero per 1, otteniamo lo stesso numero di partenza, infatti 7 : 1 = 7.
Tutte le divisioni in cui il divisore è uguale a 1, hanno come risultato il dividendo stesso. Possiamo verificare il risultato con l’operazione inversa della divisione, cioè la moltiplicazione: moltiplichiamo il risultato per il divisore e vediamo se otteniamo ancora il dividendo. Riprendiamo il nostro esempio: 7 x 1 = 7, perché sappiamo che l’1 è l’elemento neutro della moltiplicazione.
Oscar può mangiarsi tutte le caramelle: deve dividerle solo con se stesso!
Dividendo uguale a 0

Se dividiamo lo 0 per qualsiasi numero, otteniamo sempre 0. Infatti 0 : 12 = 0. Come facciamo a distribuire 0 oggetti tra più persone?
Verifichiamo il risultato sempre con la moltiplicazione: il prodotto del risultato per il divisore è uguale al dividendo? Riprendiamo il nostro esempio: 0 x 12 = 0, quindi la nostra divisione è corretta! Infatti lo 0 è l’elemento assorbente della moltiplicazione, quindi qualsiasi numero moltiplicato per 0 dà sempre 0. Questo si traduce nel fatto che 0 diviso per qualsiasi numero dà sempre 0.
Oscar è triste perché non ha niente da dividere…
Dividendo e divisore uguali

Ogni numero diviso per se stesso dà come risultato 1, infatti 8 : 8 = 1.
Possiamo verificare questo caso particolare sempre con la moltiplicazione, sfruttando nuovamente il fatto che l’1 è l’elemento neutro della moltiplicazione. Ma proviamo a ragionare sull’operazione che abbiamo appena fatto: stiamo dividendo un certo numero per lo stesso numero, cioè è come se volessimo distribuire un certo numero di cose per lo stesso numero di persone. Se vogliamo distribuire 10 caramelle a 10 persone, ne daremo una a testa!
Quattro fette di pizza per quattro mostri: una fetta ciascuno!
Divisioni fino al 100 e al 1000
Il limite sale a 100 e a 1000 e il calcolo si fa più impegnativo. Ma nessun timore: esercitandoti diventerai un campione!
Quando impariamo a fare divisioni fino a 100, ci esercitiamo a dividere numeri più piccoli, come ad esempio 50 diviso 5, che ci dà come risultato 10. Questo tipo di divisioni è utile per risolvere problemi quotidiani semplici, come dividere 60 caramelle tra 6 amici, dove ognuno riceverà 10 caramelle.
Progredendo, impariamo a fare divisioni fino a 1000, che ci permettono di lavorare con numeri più grandi e di affrontare problemi più complessi. Ad esempio, 900 diviso 30 ci dà 30. Queste divisioni sono importanti per situazioni come dividere 800 fogli di carta tra 8 classi, dove ogni classe riceverà 100 fogli.
La proprietà invariantiva della divisione
Dato che la divisione è l’operazione inversa della moltiplicazione, per verificare il risultato di una divisione possiamo utilizzare la moltiplicazione: per esempio 42 : 7 = 6 è corretto perché 6 x 7 = 42.
La divisione non ha le stesse proprietà della moltiplicazione, ma ha un’utile proprietà che abbiamo già studiato con la sottrazione, la proprietà invariantiva:
- se moltiplichiamo dividendo e divisore per lo stesso numero (diverso da 0), il risultato non cambia: 12 : 3 = 4 è come fare (12 x 3) : (3 x 3) = 36 : 9 = 4;
- se dividiamo il dividendo e il divisore per lo stesso numero (diverso da 0), il risultato non cambia: 16 : 8 = 2 è come fare (16 : 4) : (8 : 4) = 4 : 2 = 2.
Ricordati di questa proprietà per velocizzare i calcoli!
La proprietà distributiva della divisione
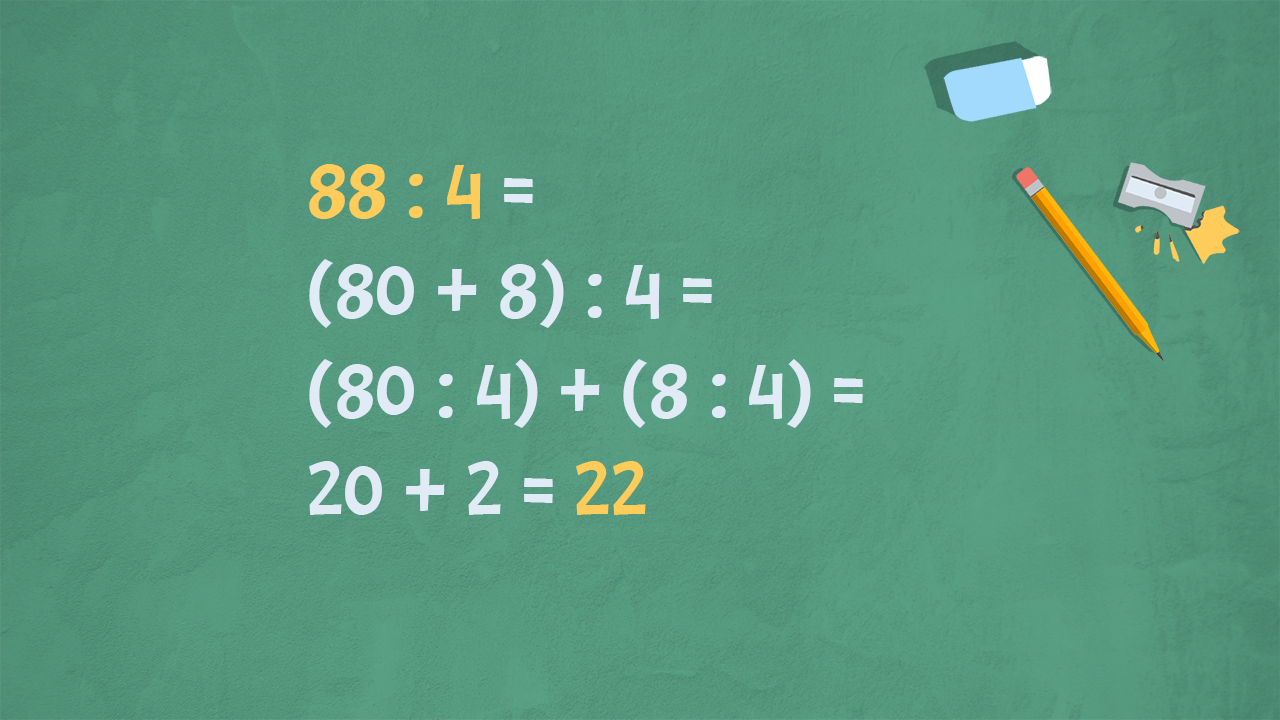
Quello che abbiamo già imparato per la moltiplicazione vale anche per la divisione: la proprietà distributiva rispetto all’addizione o alla sottrazione. Possiamo sfruttare questa proprietà per semplificare delle divisioni apparentemente difficili: scomponiamo il dividendo in una somma (o una sottrazione) e poi calcoliamo le due divisioni, spezzando così i conti.
88 : 4 = (80 + 8) : 4 = (80 : 4) + (8 : 4) = 20 + 2 = 22
Attenzione: possiamo sfruttare questa proprietà soltanto scomponendo il dividendo, non possiamo fare la stessa cosa con il divisore.
Per la divisione non valgono la proprietà commutativa e la proprietà associativa che abbiamo visto per la moltiplicazione.
Moltiplicazione e divisione per organizzare i compiti
Ripassiamo moltiplicazione e divisione!
Con il prodotto possiamo fare le somme più velocemente. Il prodotto di due numeri, infatti, equivale a sommare il primo numero tante volte quante sono indicate dal secondo numero.
Per esempio: £$ 3 \times 4 $£ (oppure £$ 3 \cdot 4 $£) è uguale a 4 volte 3, cioè £$ 3 + 3 + 3 + 3 = 12 $£.
Il quoziente tra due numeri è il più grande numero che, moltiplicato per il secondo termine, dà come risultato il primo.
Per esempio: £$ 24 : 3 = 8 $£ perché £$ 8 \cdot 3 = 24 $£.
La mappa mentale della divisione
La divisione sembra difficile, ma con il giusto esercizio non ti farà più paura. Più si fa pratica più si migliora!
Ripassa tutti gli argomenti con l’aiuto della mappa mentale.
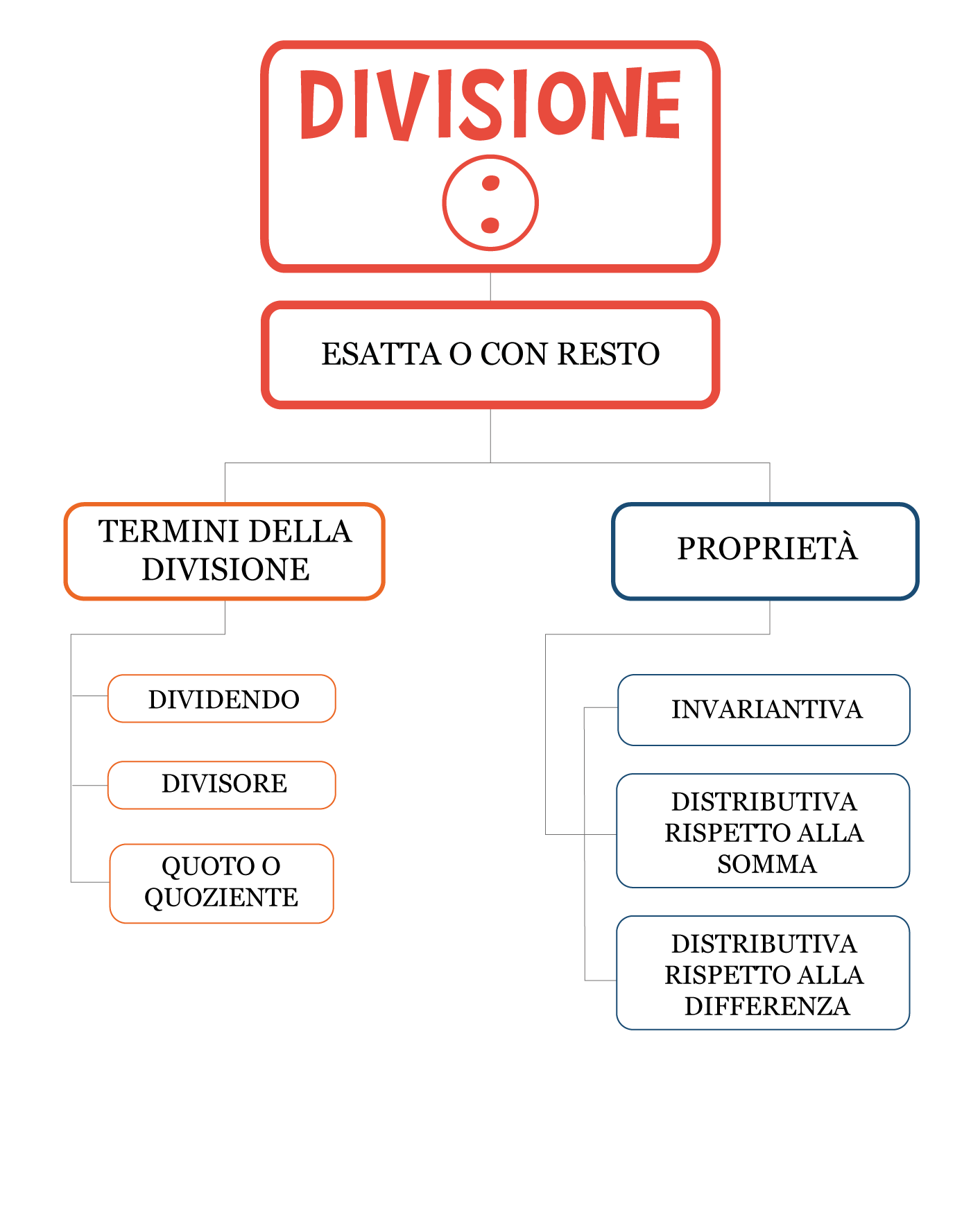
Scaricala e stampala per portarla sempre con te:
Scheda attività – le divisioni
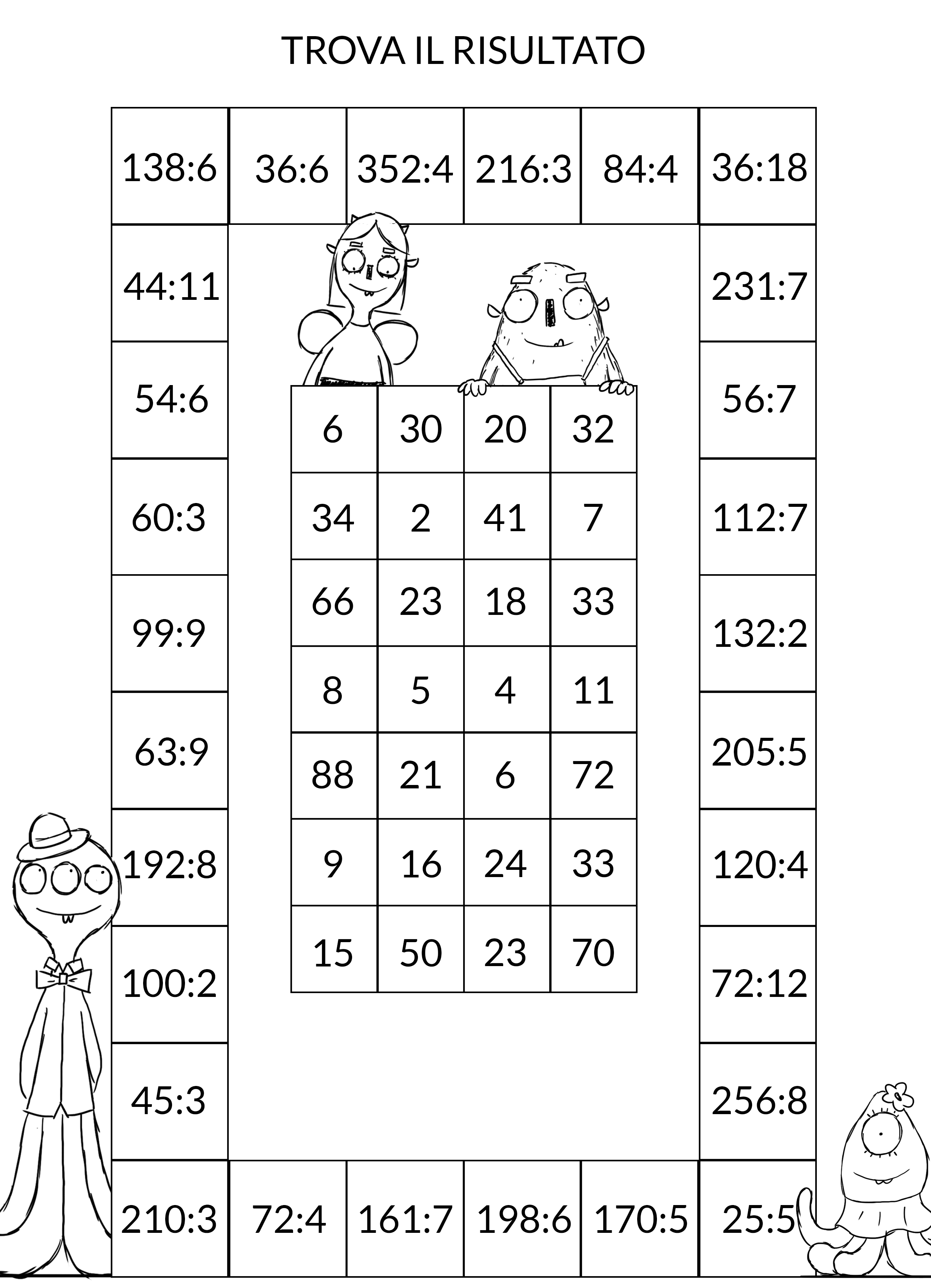
Abbiamo imparato cosa sono le divisioni. Ora è il momento di imparare qualcosa di più: come si chiamano i termini della divisione? Possiamo sempre trovare il risultato di una divisione o esistono dei casi particolari in cui non è possibile?
Con la scheda proponiamo un’attività divertente con cui prendere dimestichezza con le divisioni: un gioco per due sfidanti, una gara di abilità con le divisioni. Ciascun partecipante sceglie un colore diverso e si arma di carta e penna per risolvere le divisioni. Uno per volta, gli sfidanti risolvono una divisione del contorno esterno e colorano il risultato nel rettangolo interno. Attenzione a controllare sempre che sia il risultato corretto! Al termine verrà dichiarato il vincitore: quello che ha conquistato più caselle con il proprio colore!
Scarica qui la scheda:
Esercizi con le divisioni
Infine, tante schede con esercizi sulle divisioni, pronti da stampare e da utilizzare in classe!

Tanti esercizi e problemi con la soluzione per preparare la verifica sulle divisioni semplici.
Scarica la scheda qui:

E per finire, gli esercizi sulle divisioni esatte e divisioni con resto.
Scarica la scheda qui:
