Problema da svolgere sui triangoli e la simmetria centrale
La simmetria centrale nei triangoli è un tipo di simmetria in cui un triangolo viene mappato su se stesso attraverso una rotazione di 180 gradi intorno a un punto fisso, noto come centro di simmetria. Questo concetto può essere visualizzato immaginando di piazzare un punto, il centro di simmetria, in un luogo arbitrario rispetto al triangolo e poi ruotare il triangolo di 180 gradi attorno a quel punto. Se, dopo questa rotazione, il triangolo coincide esattamente con la sua posizione originale, allora si dice che il triangolo possiede simmetria centrale rispetto a quel punto.
In termini più tecnici, la simmetria centrale in un triangolo significa che ogni punto del triangolo, prima della rotazione, ha un corrispondente punto dopo la rotazione, tale che la linea congiungente questi due punti passa per il centro di simmetria e tale che la distanza tra ogni punto e il centro è la stessa prima e dopo la rotazione. In pratica, questo implica che il triangolo e la sua immagine ruotata sono congruenti, cioè hanno la stessa forma e dimensione, ma sono orientati in modo opposto.
Proviamo ad esercitarci insieme con un problema sui triangoli e la simmetria centrale.
- Testo del problema su triangoli e simmetria centrale
- Soluzione dei punti a), b), c) e d)
- Soluzione del punto e)
- Soluzione del punto f)
- Soluzione del punto g), h) e i)
Testo del problema su triangoli e simmetria centrale
In un sistema di riferimento cartesiano ortogonale monometrico £$ (u = 1 \text{ cm})$£ rappresenta i seguenti punti:
$$ A (0;0) \quad B (3; 0) \quad C (0; 4) $$
a) Congiungi i punti nell’ordine dato;
b) calcola la misura dei lati;
c) scrivi quale poligono ottieni e giustifica la tua risposta;
d) calcola il perimetro e l’area del poligono ottenuto £$ABC$£.
e) Disegna la figura £$A’B’C’$£ simmetrica di £$ABC$£ rispetto all’origine degli assi, calcola le coordinate dei punti ottenuti; scrivi le equazioni della simmetria (o calcolale graficamente).
f) Congiungi i punti £$C$£ con £$B’$£ e £$C’$£ con £$B$£. Considera ora il poligono £$BCB’C’$£. Di quale poligono si tratta? Ha degli assi di simmetria? A quali elementi della figura corrispondono?
g) Disegna la retta £$r$£ di equazione £$ x = -3 $£.
h) Scrivi l’equazione della retta £$ s $£ parallela all’asse £$ x $£ e passante per il punto £$ C $£; rappresentala.
i) Determina le coordinate del punto £$P$£ di intersezione fra le rette £$r$£ ed £$s$£.
Soluzione dei punti a), b), c) e d)
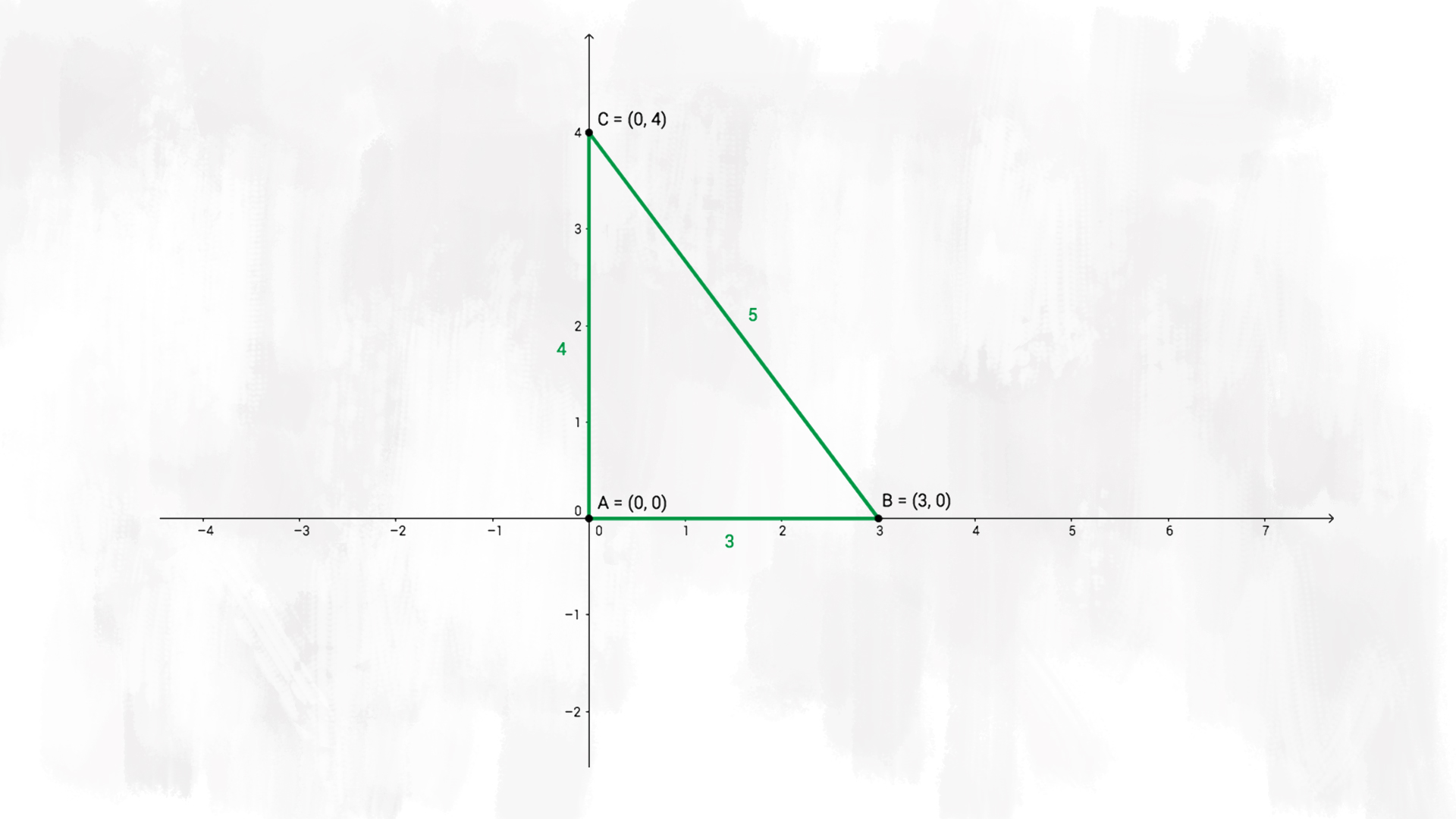
In un sistema di riferimento cartesiano ortogonale monometrico £$ (u = 1 \text{ cm})$£ rappresenta i seguenti punti:
$$ A (0;0) \quad B (3; 0) \quad C (0; 4) $$
a) Congiungi i punti nell’ordine dato;
Nell’immagine abbiamo disegnato e collegato i tre punti £$ A, B $£ e £$ C $£.
b) calcola la misura dei lati;
Per calcolare la misura del lato orizzontale, basta fare la differenza tra le ascisse. Analogamente, per trovare la misura del lato verticale, basta fare la differenza tra le ordinate. Per trovare la lunghezza del terzo lato, utilizziamo il teorema di Pitagora, che si traduce nella formula £$\overline{AB} = \sqrt{(x_B – x_A)^2+(y_B – y_A)^2}$£.
Quindi:
$$\overline{AB} = | 3 – 0 | = 3 $$ $$\overline{AC} = | 0 – 4 | = 4 $$ $$\overline{BC} = \sqrt{(0 – 3)^2+(4 – 0)^2} = 5$$
c) scrivi quale poligono ottieni e giustifica la tua risposta;
Un poligono di tre lati e tre verticiè un triangolo. Nel nostro caso, si tratta di un triangolo rettangolo. Ricordiamo che un triangolo si dice rettangolo quando ha un angolo di £$90°$£! Siccome i due cateti del triangolo si trovano su gli assi cartesiani che sono perpendicolari, siamo sicuri che il triangolo ABC è rettangolo in A (che coincide con l’origine degli assi cartesiani).
d) calcola il perimetro e l’area del poligono ottenuto £$ ABC $£.
Per trovare il perimetro del triangolo rettangolo, basta sommare i tre lati:
$$ \text{perimetro} = \overline{AB} + \overline{BC} + \overline{AC} = 3 + 5 + 4 = 12 \text{ m} $$
Calcoliamo l’area moltiplicando i due cateti del triangolo rettangolo e dividendo poi per 2:
$$A=\frac{b\times{h}}{2} = \frac{3\times{4}}{2} = 6 \text{ m}^2 $$
Soluzione del punto e)
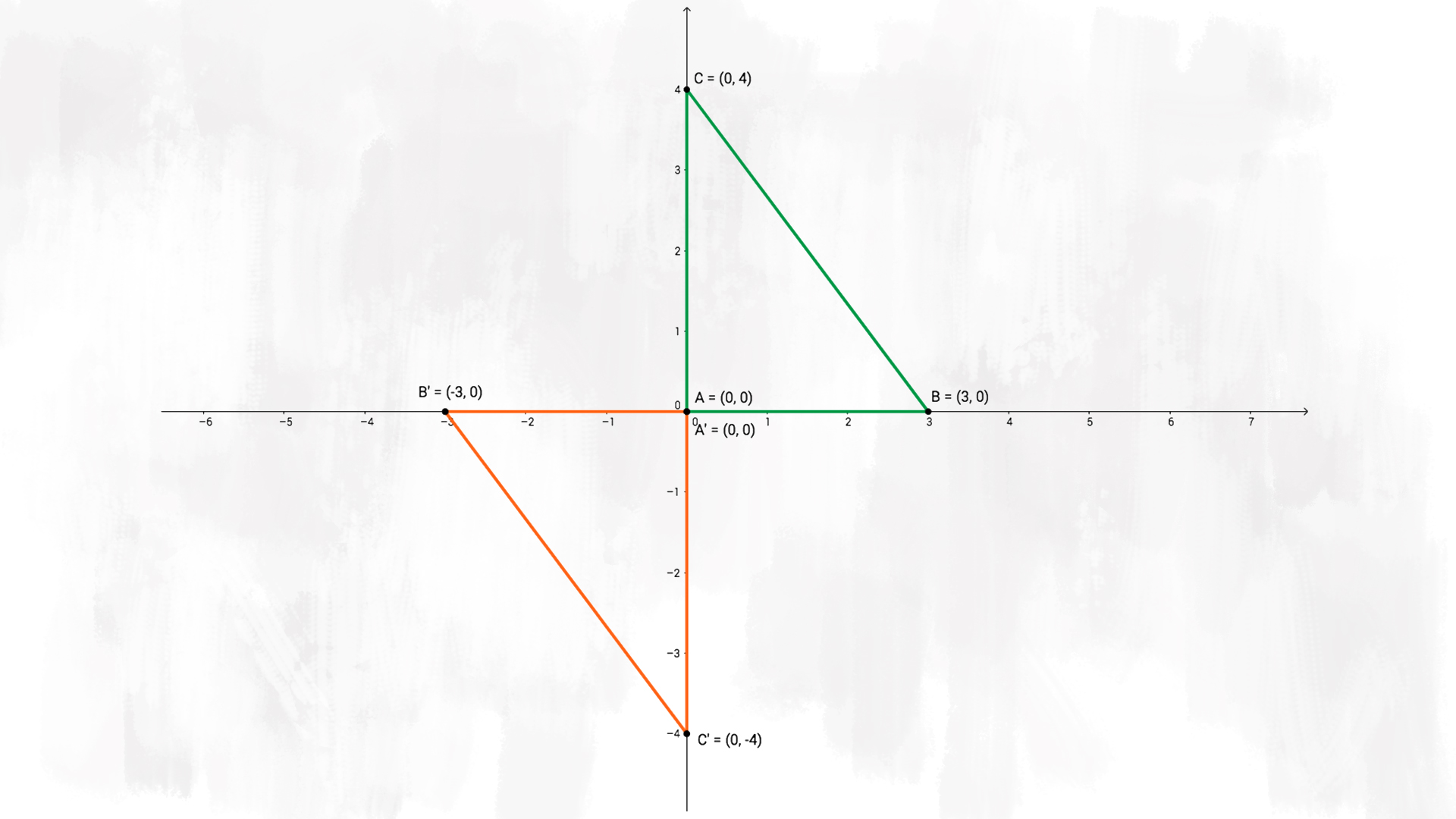
e) Disegna la figura £$A’B’C’$£ simmetrica di £$ABC$£ rispetto all’origine degli assi, calcola le coordinate dei punti ottenuti; scrivi le equazioni della simmetria (o calcolale graficamente).
Facendo la simmetria rispetto all’origine degli assi, otteniamo il triangolo arancione. Vediamo che tutti i punti hanno le stesse coordinate di quelli di partenza, ma cambiate di segno:
$$ A'(0;0) \quad B'(-3;0) \quad C'(0;-4) $$
Quindi possiamo ricavare le equazioni della simmetria:
$$ \begin{cases} x’ = -x \\ y’= -y \end{cases} $$
Soluzione del punto f)
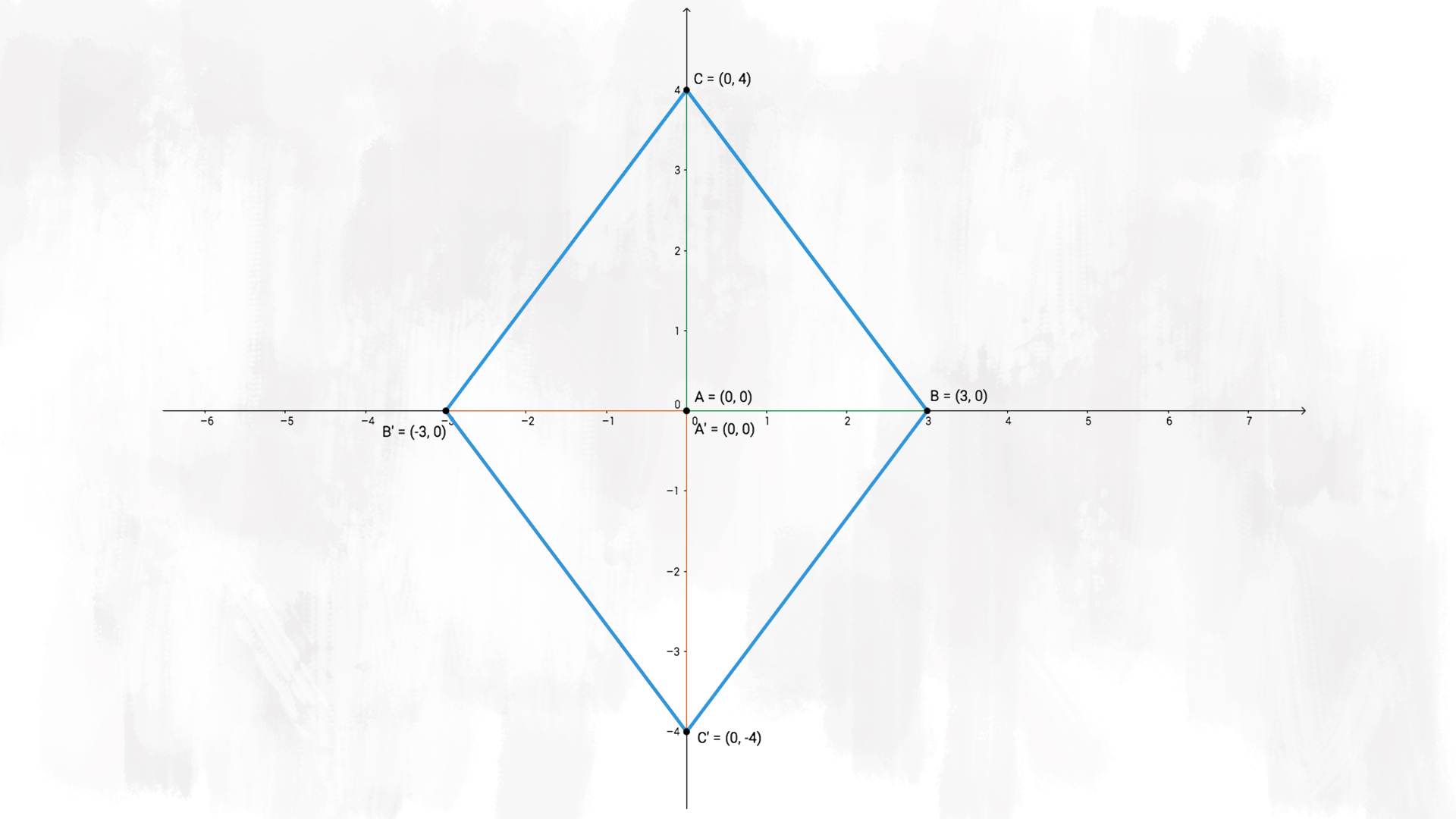
f) Congiungi i punti £$C$£ con £$B’$£ e £$C’$£ con £$B$£. Considera ora il poligono £$BCB’C’$£. Di quale poligono si tratta? Ha degli assi di simmetria? A quali elementi della figura corrispondono?
Congiugendo i lati, otteniamo un quadrilatero £$BCB’C’$£, in particolare è un rombo.
In quanto rombo, ha degli assi di simmetria che corrispondono alle sue diagonali. Nella figura, gli assi di simmetria coincidono con gli assi cartesiani. Il quadrilatero £$BCB’C’$£ è simmetrico rispetto all’asse £$ x $£ e rispetto all’asse £$ y $£.
Soluzione del punto g), h) e i)
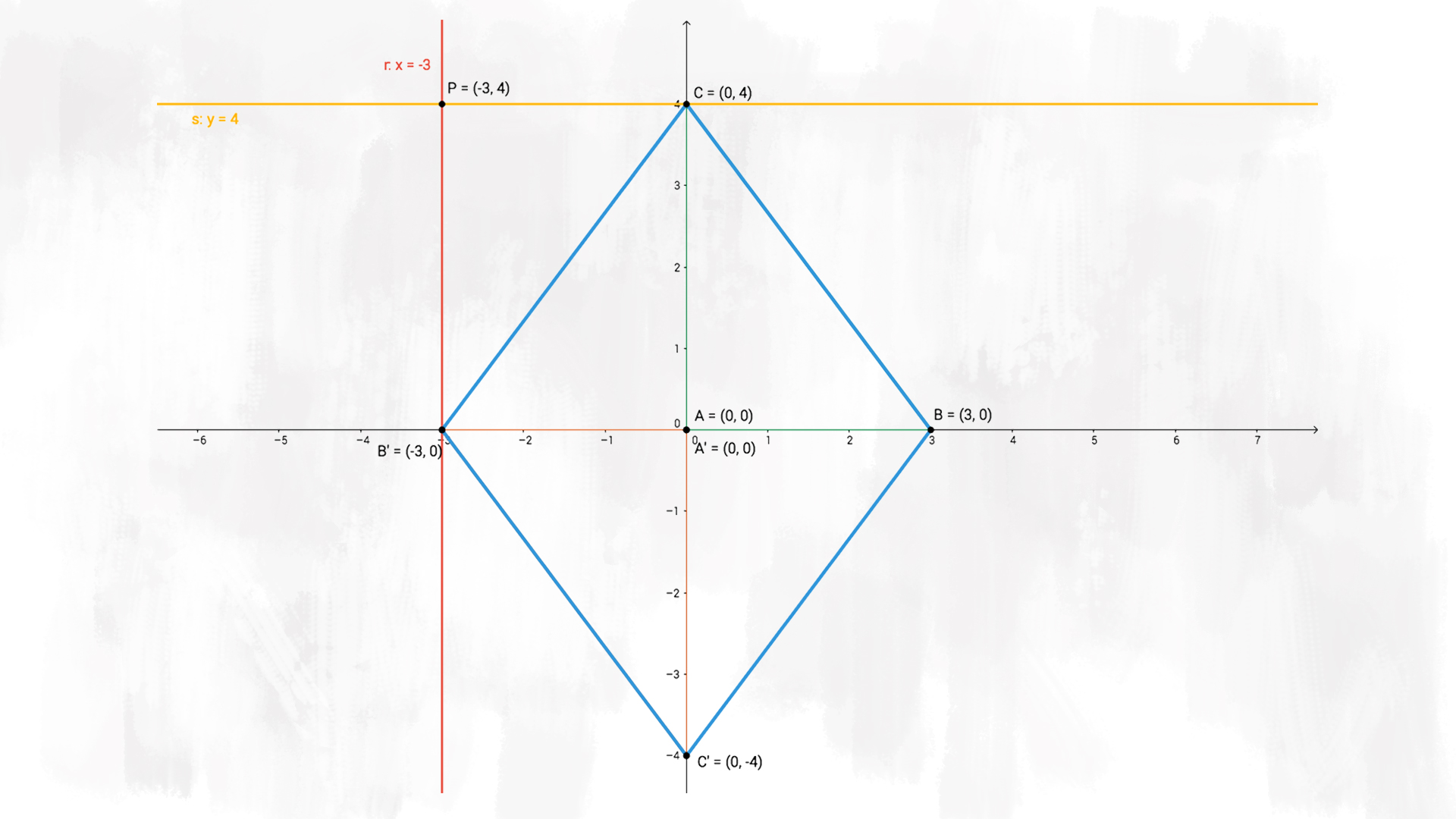
g) Disegna la retta £$r$£ di equazione £$ x = -3 $£.
La retta £$ r $£ è una retta verticale. Infatti rappresenta tutti i punti che hanno ascissa uguale a £$ -3 $£. È la retta che passa per il punto £$ B’$£ che abbiamo disegnato di rosso.
h) Scrivi l’equazione della retta £$ s $£ parallela all’asse £$ x $£ e passante per il punto £$ C $£; rappresentala.
La retta £$ s $£ è parallela all’asse £$ x $£, quindi è una retta orizzontale. È la retta formata da tutti i punti che hanno ordinata uguale a quella del punto £$ C $£, quindi è la retta £$ y = 4 $£ che abbiamo rappresentato di giallo.
i) Determina le coordinate del punto £$P$£ di intersezione fra le rette £$r$£ ed £$s$£.
Possiamo trovare le coordinate del punto £$ P $£ a occhio. Essendo l’intersezione tra la retta £$ x = -3 $£ e la retta £$ y = 4 $£, è facile capire che £$ P $£ è il punto di coordinate £$ P(-3; 4) $£.
