Problema da svolgere di geometria solida
La geometria solida è un ramo della matematica che si occupa dello studio delle proprietà e delle misure degli spazi tridimensionali e delle figure contenute in essi, come sfere, cilindri, prismi, piramidi e poliedri. A differenza della geometria piana, che si concentra sulle figure bidimensionali come linee, cerchi e poligoni, la geometria solida esplora il concetto di volume, la capacità interna di un oggetto e l’area della superficie, che rappresenta l’estensione totale dello spazio occupato dalla superficie di un solido.
La transizione dalla geometria piana alla geometria solida introduce una nuova dimensione, aggiungendo profondità alle lunghezze e alle aree studiate in due dimensioni. La geometria solida gioca un ruolo cruciale non solo nella matematica pura, ma anche in molteplici applicazioni pratiche, come l’architettura, l’ingegneria, il design e la fisica, fornendo gli strumenti necessari per comprendere e manipolare l’ambiente fisico che ci circonda.
Proviamo ad esercitarci con un problema da svolgere.
- Testo del problema di geometria solida
- Soluzione ai punti 1), 2), 3), 4), 5)
- Soluzione al punto 6)
- Soluzione al punto 7)
- Soluzione ai punti 8) e 9)
Testo del problema di geometria solida
Un parallelepipedo rettangolo ha le dimensioni di base che misurano rispettivamente £$ 28 \text{ dm} $£ e £$ 24 \text{ dm} $£; l’altezza del parallelepipedo misura £$ 20 \text{ dm} $£. Calcola:
1) il perimetro di base;
2) l’area della superficie laterale;
3) l’area della superficie di base;
4) l’area della superficie totale;
5) il volume.
Considera ora un prisma retto che ha per base un triangolo isoscele. Il perimetro del triangolo misura £$ 64 \text{ dm} $£ e la sua base è i £$ \dfrac 65 $£ di ciascun lato obliquo. L’area della superficie laterale del prisma misura £$ 1792 \text{ dm}^2 $£. Calcola:
6) il volume del prisma.
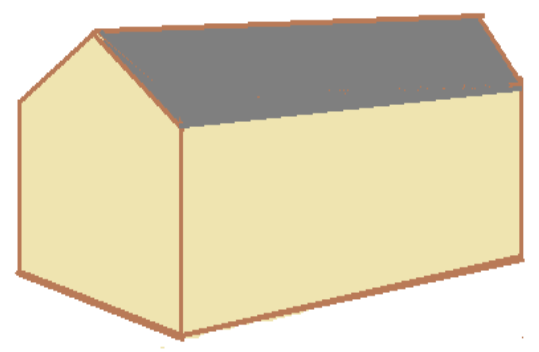
7) Calcola la misura, in £$ \text{m}^2 $£, della superficie totale della casetta, comprensiva del pavimento.
Il tetto della casetta viene rivestito con una guaina impermeabile che è venduta solamente in rotoli da £$ 10 \text{ m}^2 $£ ciascuno.
8) Quanti £$ \text{m}^2 $£ bisogna rivestire?
9) Quanti rotoli occorre comprare?
Soluzione ai punti 1), 2), 3), 4), 5)
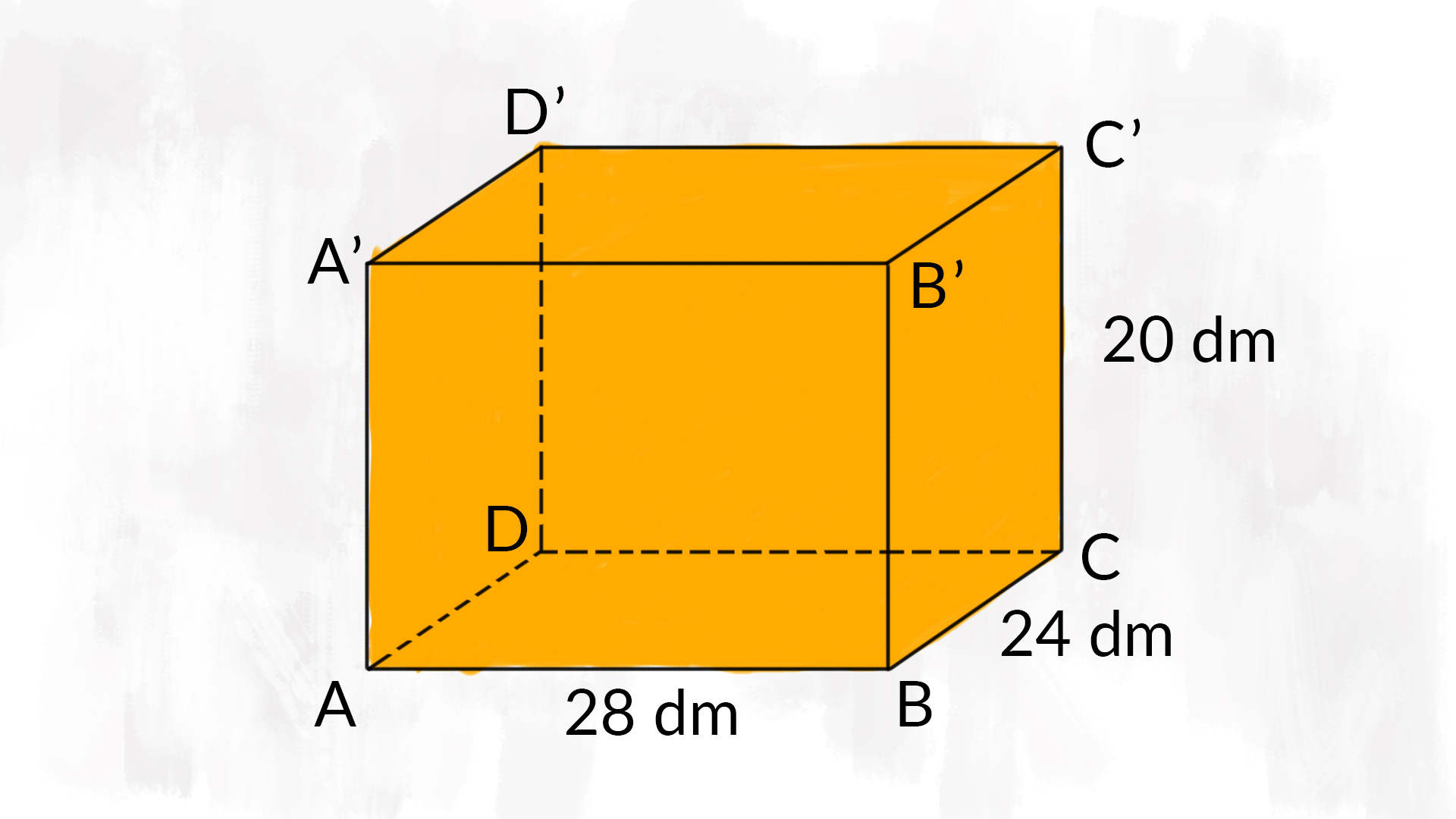
Facciamo un disegno del parallelepipedo e rispondiamo alle prime domande.
Un parallelepipedo rettangolo ha le dimensioni di base che misurano rispettivamente £$ 28 \text{ dm} $£ e £$ 24 \text{ dm} $£; l’altezza del parallelepipedo misura £$ 20 \text{ dm} $£. Calcola:
1) il perimetro di base;
£$ \overline{AB} = 28 \text{ dm} $£ e £$ \overline{BC} = 24 \text{ cm} $£. Il solido è un parallelepipedo, quindi la base è un rettangolo:
$$ \text{perimetro} = (28 \text{ dm} + 24 \text{ dm}) \cdot 2 = 104 \text{ dm} $$
2) l’area della superficie laterale;
Ricordi come si calcola la superficie laterale di un parallelepipedo o, in generale, di un prisma? Moltiplichiamo il perimetro di base per l’altezza:
$$ S_{\ell_1} = 104 \text{ dm} \cdot 20 \text{ dm} = 2080 \text{ dm}^2 $$
3) l’area della superficie di base;
L’area di un rettangolo è uguale al prodotto della base per l’altezza, quindi:
$$ A_{b_1} = 28 \text{ dm} \cdot 24 \text{ dm} = 672 \text{ dm}^2 $$
4) l’area della superficie totale;
La superficie totale di un parallelepipedo è data dalla somma delle due aree di base e della superficie laterale:
$$ S_{\text{tot}_1} = 2080 \text{ dm}^2 + 2 \cdot 672 \text{ dm}^2 = 3424 \text{ dm}^2 $$
5) il volume.
Per calcolare il volume di un parallelepipedo, basta moltiplicare tra loro le tre dimensioni:
$$ V_1 = 28 \text{ dm} \cdot 24 \text{ dm} \cdot 20 \text{ dm} = 13 \, 440 \text{ dm}^3 $$
Soluzione al punto 6)
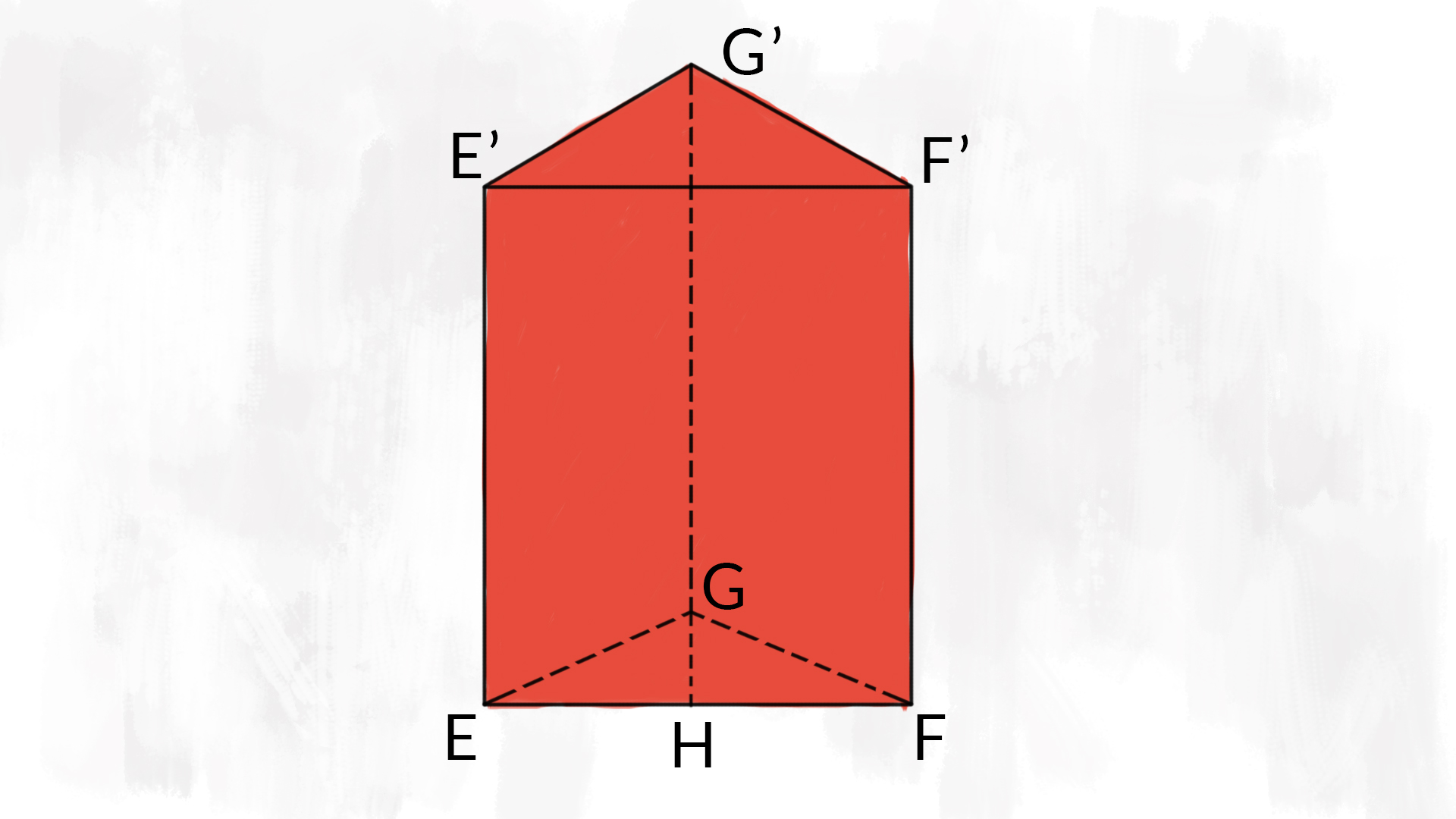
Anche in questo caso, aiutiamoci con un disegno.
Considera ora un prisma retto che ha per base un triangolo isoscele. Il perimetro del triangolo misura £$ 64 \text{ dm} $£ e la sua base è i £$ \dfrac 65 $£ di ciascun lato obliquo. L’area della superficie laterale del prisma misura £$ 1792 \text{ dm}^2 $£. Calcola:
6) il volume del prisma.
Per rispondere a questa domanda, dobbiamo fare qualche conticino. Occupiamoci subito di trovare la misura dei lati di base. Sappiamo che la base del triangolo isoscele è uguale ai £$ \dfrac 65 $£ dei due lati obliqui. Quindi, chiamando £$ x $£ i due lati obliqui, possiamo scrivere che £$ x + x + \dfrac 65 x = 64 \text{ dm} $£. Possiamo risolvere l’equazione e ricavare la misura di ciascun lato obliquo, quindi della base del triangolo. Oppure, possiamo ricordarci che il perimetro di questo triangolo è la somma di 5 + 5 + 6 parti uguali, cioè di 16 parti. Dividendo £$ \dfrac{64}{16} = 4 \text{ dm} $£ troviamo la misura di ciascuna di queste parti. Quindi £$ \overline{EF} = 6 \cdot 4 \text{ dm} = 24 \text{ dm} $£. Di conseguenza £$ \overline{EG} = \overline{FG} = \dfrac{64-24}{2} = 20 \text{ dm} $£.
Dividiamo in due la base: £$ \overline{EH} = \dfrac{24}{2} \text{ dm} = 12 \text{ dm} $£.
Applicando il teorema di Pitagora, possiamo trovare la misura dell’altezza: £$ \overline{GH} = \sqrt{20^2 – 12^2} = \sqrt{ 400 – 144} = \sqrt{256} = 16 \text{ dm} $£.
L’area di base di questo prisma triangolare è:
$$ A_{b_2} = \frac{24 \cdot 16}{2} = 192 \text{ dm}^2 $$
Troviamo quindi la misura dell’altezza del prisma! Basta dividere la superficie laterale per il perimetro di base:
$$ \overline{EE’} = \frac{1792}{64}= 28 \text{ dm} $$
A questo punto possiamo calcolare il volume:
$$ V_2 = 192 \text{ dm}^2 \cdot 28 \text{ dm} = 5376 \text{ dm}^3 $$
Soluzione al punto 7)
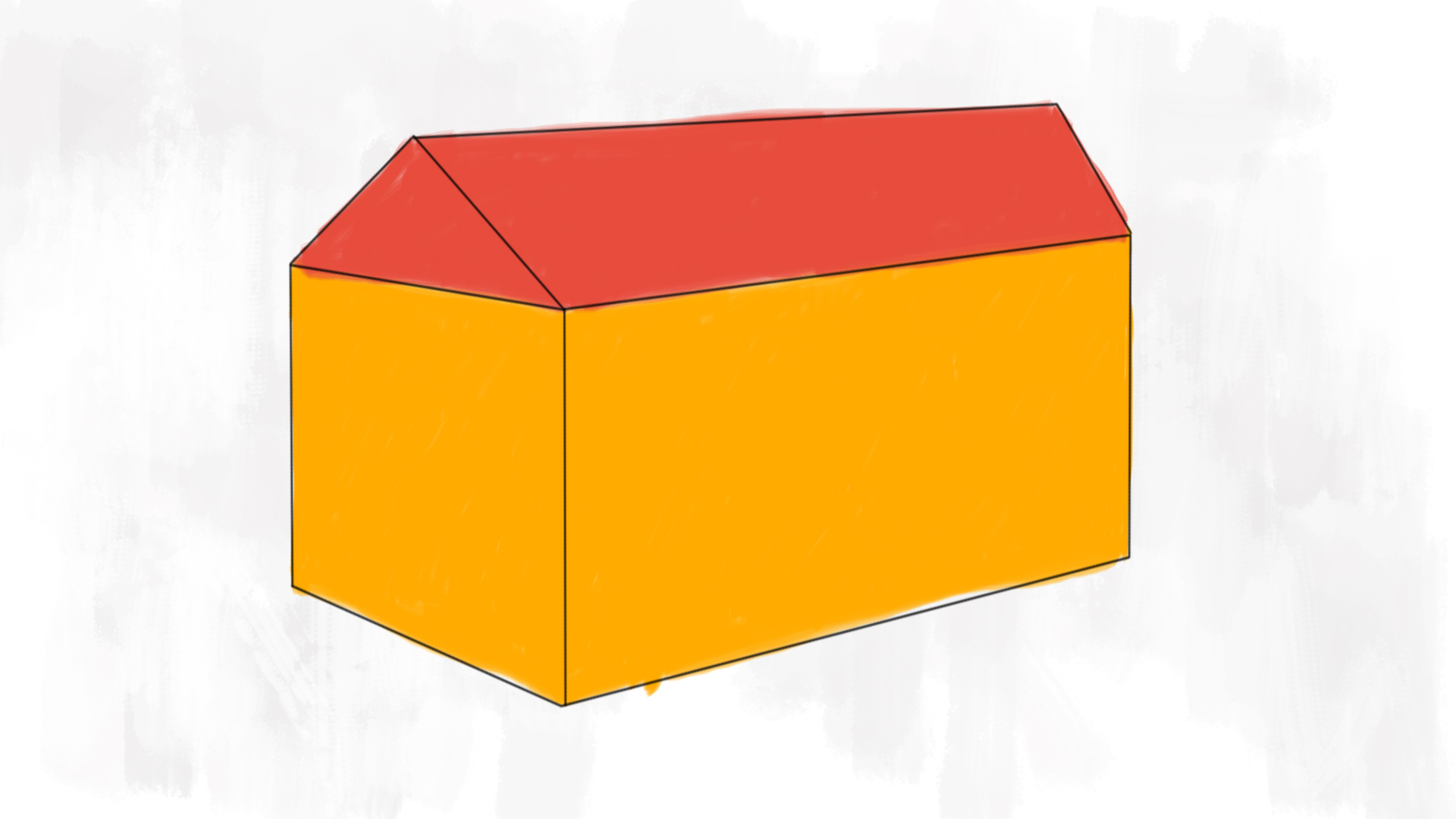
Supponi che una casetta in legno per il ricovero degli attrezzi in giardino sia costituita dal precedente parallelepipedo rettangolo sormontato dal prisma retto in modo tale che la faccia laterale più estesa (cioè con superficie maggiore) del prisma coincida perfettamente con la faccia superiore del parallelepipedo come indicato nella figura.
7) Calcola la misura, in £$ \text{m}^2 $£, della superficie totale della casetta, comprensiva del pavimento.
Osserviamo la figura. Dobbiamo calcolare la superficie totale del solido composto dal parallelepipedo e da prisma a base triangolare. La superficie totale non è uguale alla somma delle due superfici, perché una delle facce è in comune! Osserva bene la figura: noterai che, per sommare la superficie totale di questa casetta, è sufficiente sommare la superficie laterale del parallelepipedo e la superficie totale del prisma. Infatti la faccia nascosta corrisponde alla base del parallelepipedo ma, invece di sommarla e poi sottrarla, possiamo considerarla come parte della superficie totale del prisma.
Troviamo prima la superficie totale del prisma:
$$ S_{\text{tot}_2} = S_{\ell_2} + 2\cdot A_{b_2} = 1792 \text{ dm}^2 + 2\cdot 192 \text{ dm}^2 = 2176 \text{ dm}^2 $$
Ora sommiamola alla superficie laterale del parallelepipedo per trovare la superficie totale della casetta di legno:
$$ S_{\text{tot casetta}} = S_{\ell_1} + S_{\text{tot}_2} = 2080 \text{ dm}^2 + 2176 \text{ dm}^2 = 4256 \text{ dm}^2 $$
La domanda, però, richiede di trovare la misura dela superficie in metri quadrati. Dobbiamo fare un’equivalenza! Fai attenzione! Stiamo utilizzando le misure di superficie, quindi il quadrato di una misura di lunghezza. Per passare da £$ \text{dm}^2 $£ a £$ \text{m}^2 $£ dobbiamo dividere per 100 e non per 10:
$$ S_{\text{tot casetta}} = 4256 \text{ dm}^2 = 42,56 \text{ m}^2 $$
Soluzione ai punti 8) e 9)
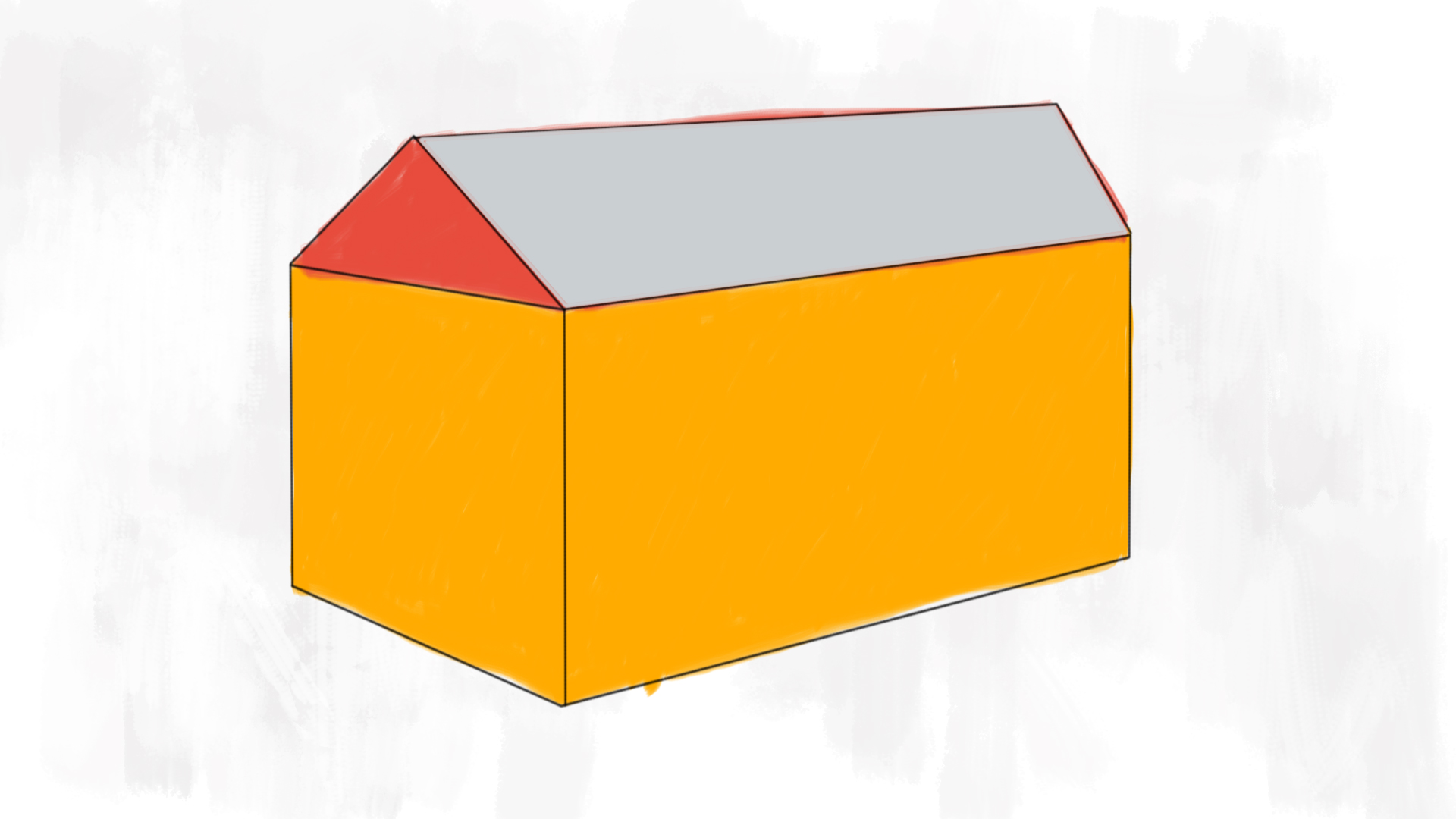
Il tetto della casetta viene rivestito con una guaina impermeabile che è venduta solamente in rotoli da £$ 10 \text{ m}^2 $£ ciascuno.
8) Quanti £$ \text{m}^2 $£ bisogna rivestire?
Il tetto della casetta è formato dalle due facce del prisma triangolare che hanno per base i lati obliqui. Quindi le due facce che compongono il tetto hanno una superficie di:
$$ S_{\text{tetto}} = 2 \cdot 20 \cdot 28 = 1120 \text{ dm}^2 $$
Dobbiamo quindi rivestire £$ 1120 \text{ dm}^2 = 11,20 \text{ m}^2 $£ di tetto.
9) Quanti rotoli occorre comprare?
Ogni rotolo misura £$ 10 \text{ m}^2 $£. Dobbiamo rivestire una superficie di £$ 11,20 \text{ m}^2 $£ che è maggiore della quantità di guaina impermeabile presente in un rotolo. Quindi occorre comprare 2 rotoli per completare il rivestimento.
