Poligoni e simmetria assiale per l'esame di terza media
I poligoni, figure geometriche chiuse composte da segmenti di retta, sono oggetti familiari, come quadrati, rettangoli e triangoli, che incontriamo nella vita quotidiana.
La simmetria assiale può essere spiegata in modo molto semplice: un poligono è simmetrico rispetto a una linea se, piegandolo lungo quella linea, le due metà coincidono perfettamente.
Prova a risolvere questo problema di geometria analitica per prepararti all’esame di terza media. Ripassa poligoni e simmetria assiale e rispondi alle domande. Segui il procedimento: allenarsi è il modo migliore per raggiungere i risultati!
- Argomenti da ripassare su poligoni e simmetria assiale
- Testo del problema su poligoni e simmetria assiale
- Soluzione ai punti a) e b)
- Soluzione ai punti c), d) ed e)
- Soluzione al punto f)
- Soluzione al punto g)
- Soluzione al punto h), i) e j)
- Soluzione al punto k), l) e m)
Argomenti da ripassare su poligoni e simmetria assiale
Per risolvere questo problema dell’esame di terza media, ripassa poligoni e simmetria assiale, in particolare:
- coordinate dei punti sul piano cartesiano
- lunghezza dei segmenti sul piano cartesiano
- perimetro e area di un rettangolo
- proprietà dei poligoni regolari
- lunghezza di una circonferenza
- area di un cerchio
- disegnare una retta conoscendo la sua equazione, o come trovare l’equazione di una retta specifica.
Testo del problema su poligoni e simmetria assiale
a) In un sistema di riferimento cartesiano ortogonale monometrico £$(1 \text{ u} = 1 \text{ cm}) $£ individua i punti di coordinate:
$$ A(+2;+1) \quad B (+14; +1) \quad C (+14; +6) \quad D ( +2; +6) $$
b) Congiungi i punti nell’ordine dato e scrivi il nome del poligono £$F$£ ottenuto.
c) Calcola la misura dei lati.
d) Calcola la misura del perimetro e l’area del poligono £$ F$£.
e) Calcola la misura della diagonale del poligono £$F$£.
f) Rappresenta il poligono £$F’$£ di vertici £$ A’B’C’D’ $£ simmetrico di £$F$£ rispetto all’asse delle ascisse. Scrivi le coordinate dei vertici della figura £$ F’ $£. Scrivi le equazioni di simmetria o spiega come cambiano le coordinate dei vertici del poligono simmetrico £$F’$£ rispetto a quelle del poligono di partenza £$F$£.
g) Congiungi i punti £$D$£ con £$D’$£ e £$C’$£ con £$C$£. Considera ora il poligono £$ D’C’CD $£ ed indicalo con £$Q$£. Di quale poligono si tratta?
h) Disegna la circonferenza inscritta nel poligono £$Q$£ e scrivi le coordinate del centro £$P$£.
i) Calcola la lunghezza della circonferenza e l’area del cerchio.
j) Spiega perché si può inscrivere una circonferenza nel poligono £$Q$£.
k) Disegna la retta £$t$£ di equazione £$ y = +3x $£. Quale relazione osservi tra la retta £$t$£ e il poligono £$Q$£?
l) Disegna e scrivi l’equazione della retta £$ r$£ passante per il lato £$ D’C’ $£.
m) Scrivi le coordinate di £$ N $£ punto d’intersezione tra la retta £$t$£ e la retta £$r$£.
Soluzione ai punti a) e b)
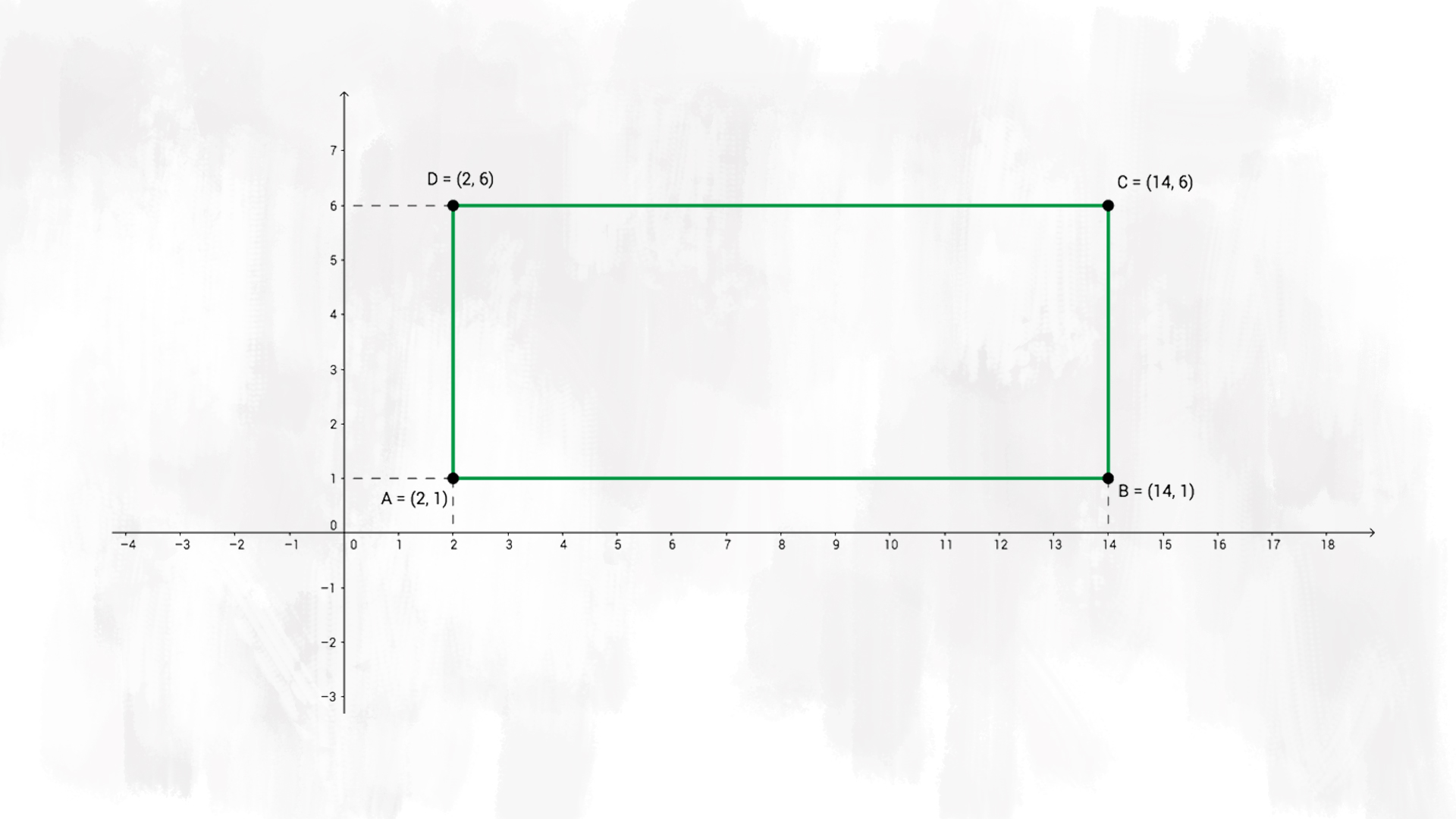
Rappresentiamo il piano cartesiano in modo che l’unità di misura corrisponda ad £$ 1 \text{ cm} $£.
a) In un sistema di riferimento cartesiano ortogonale monometrico £$(1 \text{ u} = 1 \text{ cm}) $£ individua i punti di coordinate:
$$ A(+2;+1) \quad B (+14; +1) \quad C (+14; +6) \quad D ( +2; +6) $$
Cerchiamo tutti i punti richiesti. Ricorda: un punto del piano cartesiano si rappresenta con due coordinate. La prima coordinata indica l’ascissa, cioè indica di quante unità dobbiamo spostarci a destra (se è un numero positivo) o a sinistra (se è un numero negativo) a partire dall’origine £$ O $£. La seconda coordinata indica l’ordinata, cioè di quante unità dobbiamo spostarci verso l’alto (se è un numero positivo) o verso il basso (se è un numero negativo) a partire dall’origine £$ O $£. Per esempio, per trovare £$ A $£ dobbiamo spostarci a destra di due unità e in alto di una unità.
b) Congiungi i punti nell’ordine dato e scrivi il nome del poligono £$F$£ ottenuto.
Congiungendo i quattro punti otteniamo un rettangolo.
Soluzione ai punti c), d) ed e)
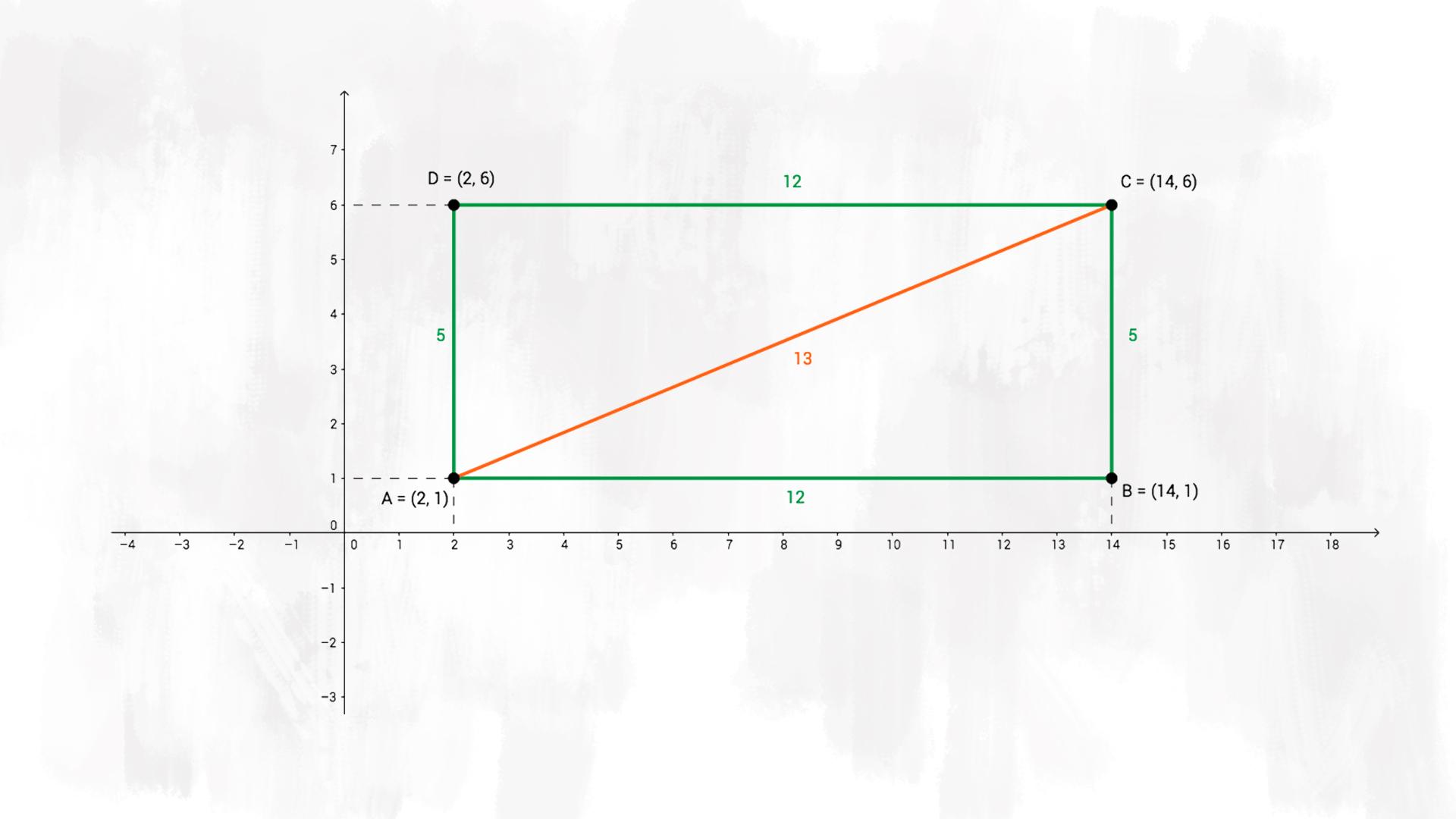
c) Calcola la misura dei lati.
Il rettangolo £$ F $£ ha i lati uguali e paralleli a due a due. Essendo segmenti orizzontali e verticali, è facile trovare la loro misura sul piano cartesiano. Basta fare una semplice differenza:
$$ \overline{AB} = \overline{DC} = 14 \text{ u} – 2 \text{ u} = 12 \text{ u} = 12 \text{ cm} $$ $$ \overline{AD} = \overline{BC} = 6 \text{ u} – 1 \text{ u} = 5 \text{ u} = 5 \text{ cm} $$
d) Calcola la misura del perimetro e l’area del poligono £$ F$£.
Possiamo quindi trovare facilmente il perimetro del rettangolo:
$$ \text{perimetro} = 2 \cdot (12 \text{ cm} + 5 \text{ cm}) = 2 \cdot 17 \text{ cm} = 34 \text{ cm} $$
Mentre l’area misura:
$$ \text{Area} = 12 \text{ cm} \cdot 5 \text{ cm} = 60 \text{ cm}^2 $$
e) Calcola la misura della diagonale del poligono £$F$£.
Per trovare la misura della diagonale dobbiamo servirci del teorema di Pitagora: la diagonale, infatti, corrisponde all’ipotenusa del triangolo rettangolo che ha per cateti la base e l’altezza del rettangolo.
$$ \overline{AC} = \sqrt{(12 \text{ cm})^2 + (5 \text{ cm})^2} = \sqrt{144 \text{ cm}^2 + 25 \text{ cm}^2} = \\ = \sqrt{169 \text{ cm}^2} = 13 \text{ cm} $$
Soluzione al punto f)
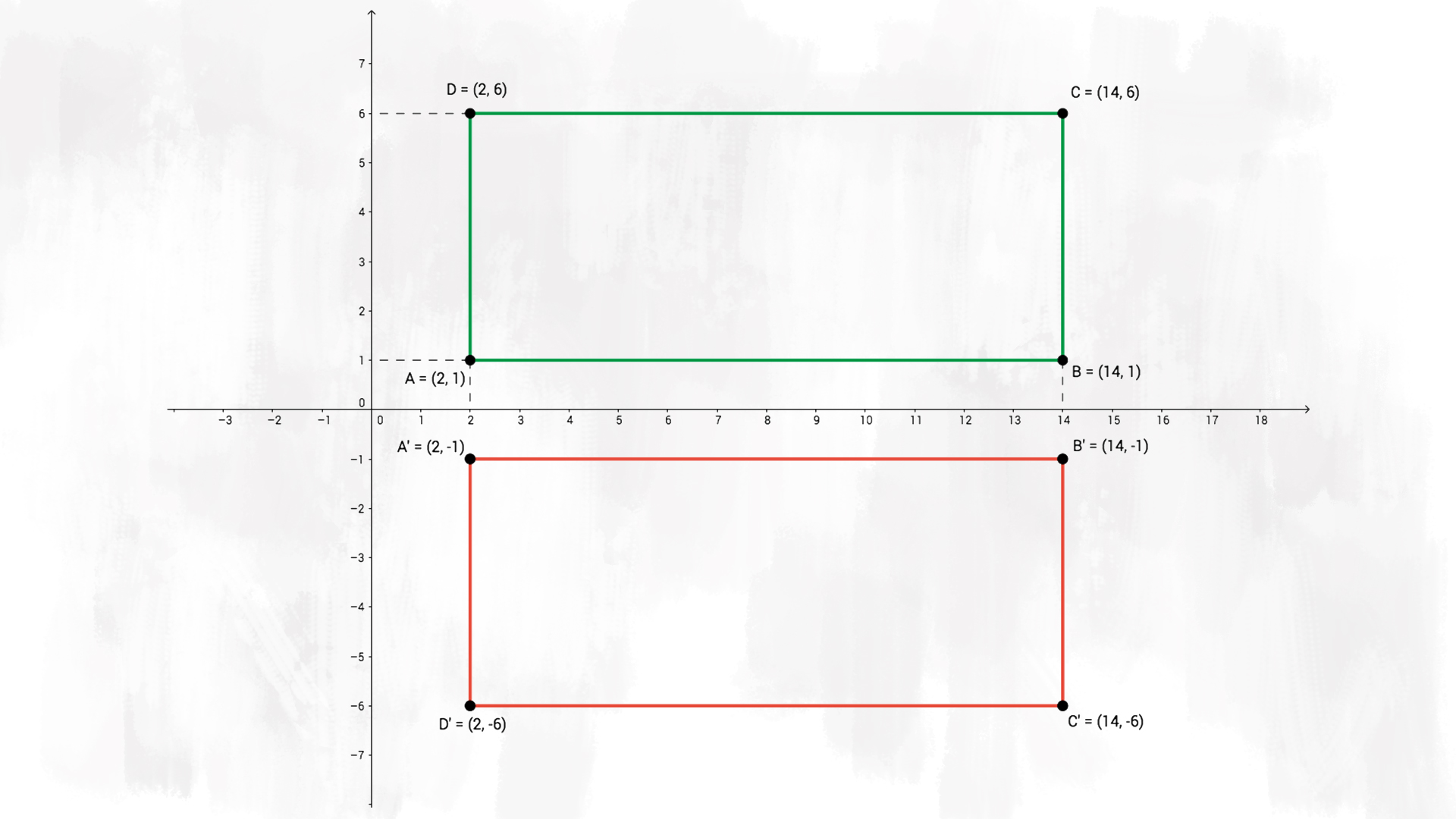
f) Rappresenta il poligono £$F’$£ di vertici £$ A’B’C’D’ $£ simmetrico di £$F$£ rispetto all’asse delle ascisse.
Per rappresentare questo poligono, immaginiamo di piegare il piano cartesiano lungo l’asse £$ x $£ e ricalchiamo la forma nel IV quadrante, come vedi nella figura.
Scrivi le coordinate dei vertici della figura £$ F’ $£.
Il nuovo rettangolo £$ F’ $£ ha per vertici £$ A’B’C’D’ $£ che hanno la stessa ascissa dei punti £$ ABCD $£, ma ordinata opposta:
$$ A'(+2; -1) \quad B'(+14; -1) \quad C'(+14; -6) \quad D'(+2; -6) $$
Scrivi le equazioni di simmetria o spiega come cambiano le coordinate dei vertici del poligono simmetrico £$F’$£ rispetto a quelle del poligono di partenza £$F$£.
Come abbiamo già detto, le coordinate dei vertici del poligono simmetrico £$ F’ $£ cambiano solo nell’ordinata. L’ascissa resta invariata. Quindi le equazioni di simmetria sono:
$$ \begin{cases} x’ = x \\ y’ = -y \end{cases} $$
Soluzione al punto g)
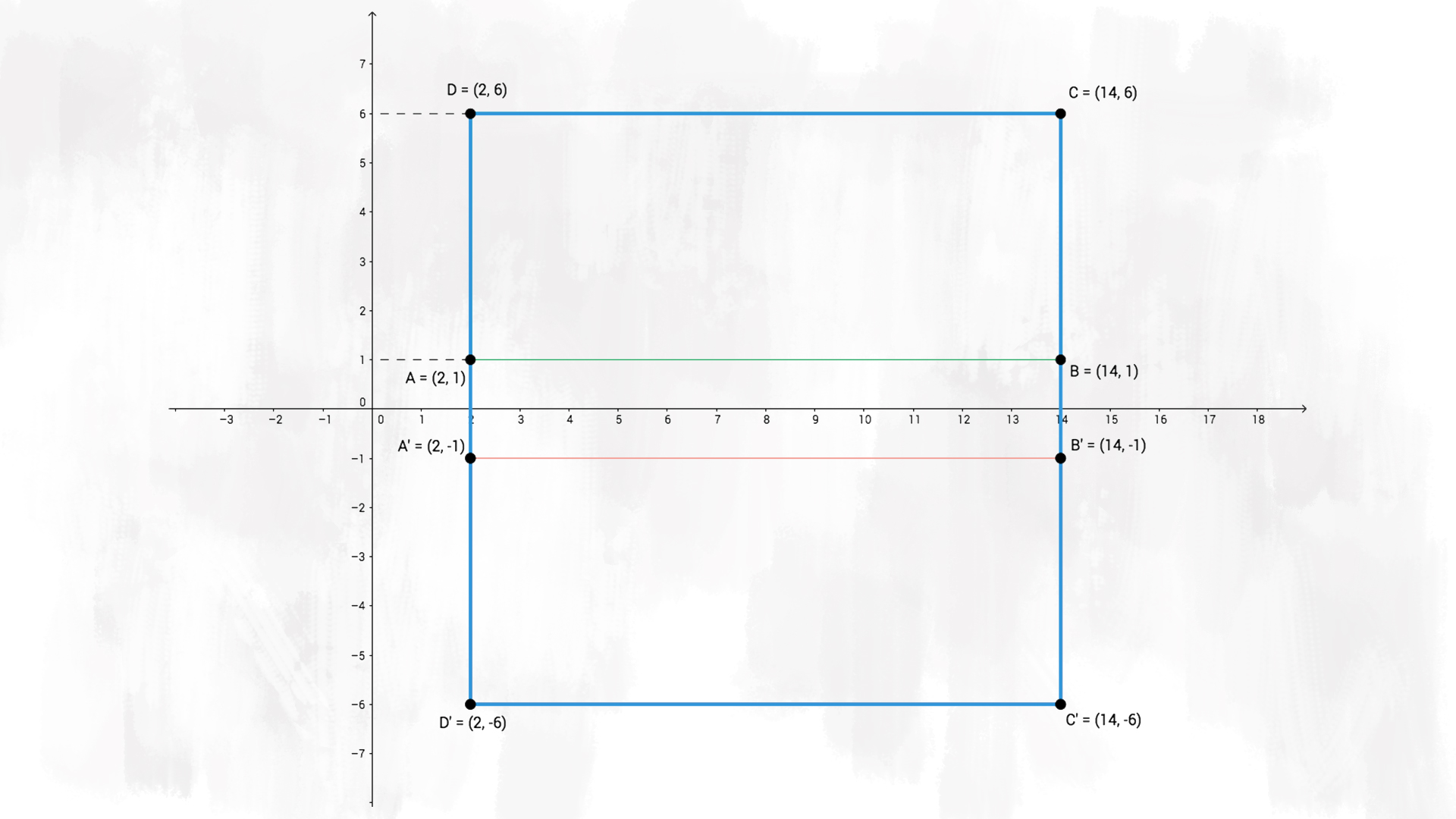
g) Congiungi i punti £$D$£ con £$D’$£ e £$C’$£ con £$C$£. Considera ora il poligono £$ D’C’CD $£ ed indicalo con £$Q$£. Di quale poligono si tratta?
Sicuramente il poligono £$ Q $£ è ancora un parallelogramma: ha i lati uguali e paralleli a due a due. Ma di che parallelogramma si tratta?
Sappiamo che £$ \overline{DC}= \overline{D’C’} = 12 \text{ cm} $£, troviamo la lunghezza degli altri due lati:
$$ \overline{DD’} = \overline{CC’} = 6 \text{ u} – ( -6 \text{ u}) = 12 \text{ u} = 12 \text{ cm} $$
È un poligono con quattro lati congruenti! Il poligono £$ Q $£ è un quadrato!
Soluzione al punto h), i) e j)
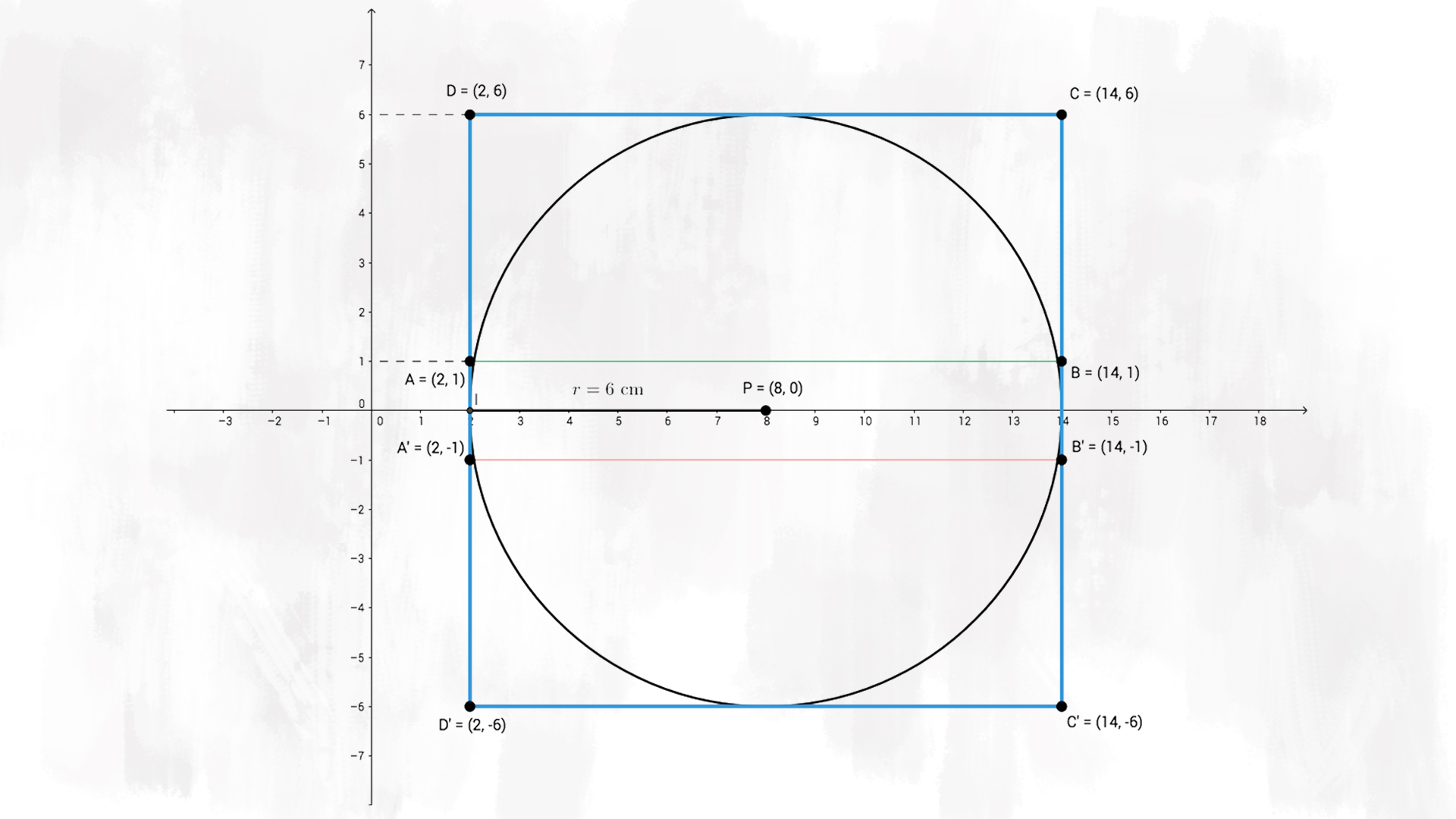
h) Disegna la circonferenza inscritta nel poligono £$Q$£ e scrivi le coordinate del centro £$P$£.
Il centro della circonferenza corrisponde con il centro del quadrato, quindi è il punto che si trova alla stessa distanza da tutti i quattro lati del poligono £$ Q $£. Il punto £$ P $£, quindi, ha coordinate £$ P(+8; 0) $£.
i) Calcola la lunghezza della circonferenza e l’area del cerchio.
Sappiamo che il raggio della circonferenza inscritta in un quadrato è uguale alla metà del lato, cioè: £$ r = \frac{12}{2} \text{ cm} = 6 \text{ cm} $£. Se non ricordi o non riesci a visualizzare questa proprietà dal disegno, basta fare un semplice calcolo: il centro della circonferenza è £$ P(+8;0) $£, quindi il raggio misura £$ r = 8 \text{ u} – 2 \text{ u} = 6 \text{ u} = 6 \text{ cm} $£. Ora che conosciamo il raggio, possiamo trovare la lunghezza della circonferenza e l’area del cerchio:
$$ \text{Circonferenza} = 2 \pi \cdot 6 \text{ cm} = 12 \pi \text{ cm} \simeq 37,68 \text{ cm} $$ $$ \text{Area cerchio} = \pi \cdot (6\text{ cm})^2 = 36 \pi \text{ cm}^2 \simeq 113,04 \text{ cm}^2 $$
j) Spiega perché si può inscrivere una circonferenza nel poligono £$Q$£.
Possiamo inscrivere una circonferenza nel poligono £$ Q $£ perché, essendo un quadrato, è un poligono regolare. Tutti i poligoni regolari si possono sempre inscrivere e circoscrivere ad una circonferenza.
Soluzione al punto k), l) e m)
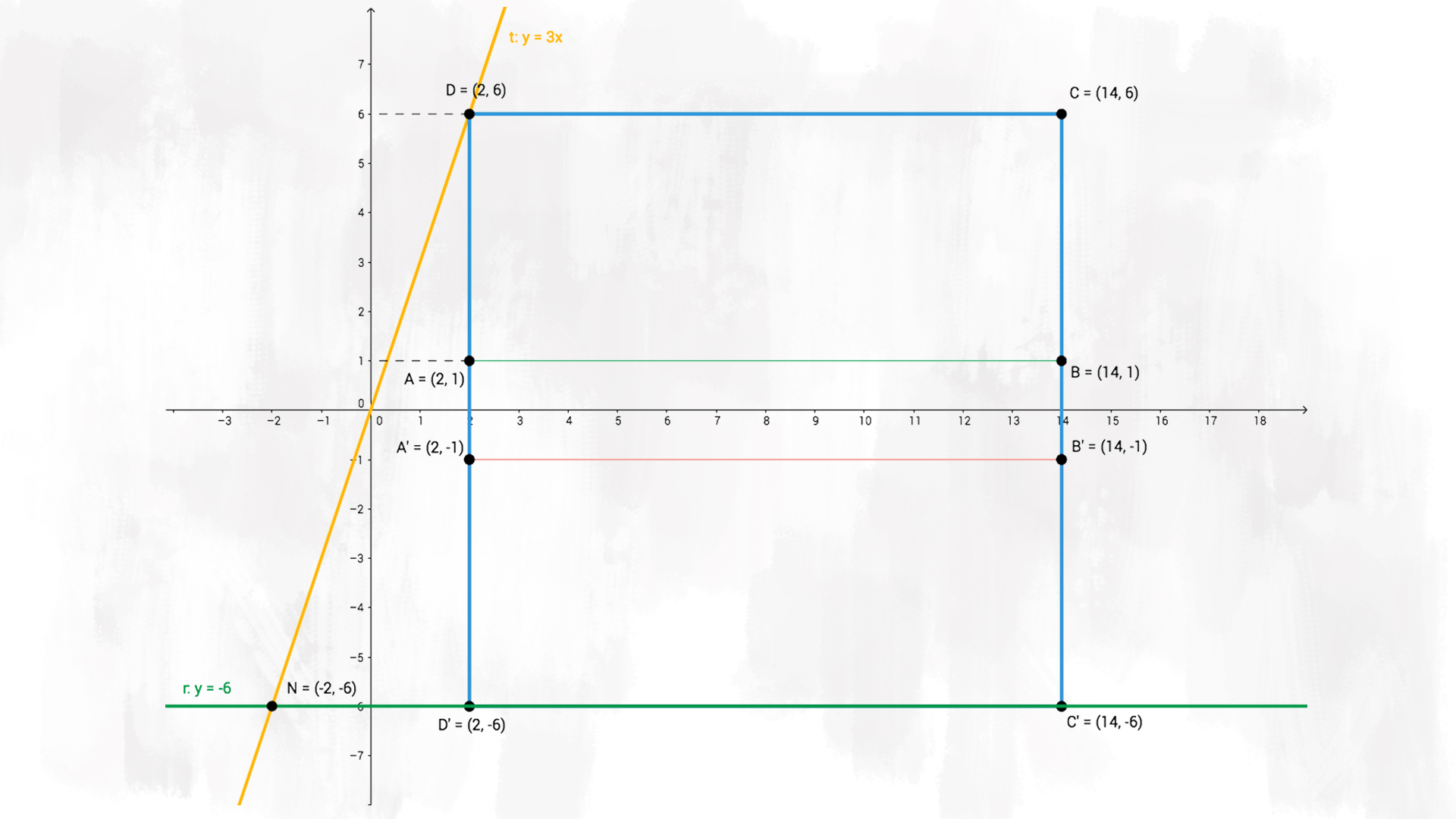
k) Disegna la retta £$t$£ di equazione £$ y = +3x $£. Quale relazione osservi tra la retta £$t$£ e il poligono £$Q$£?
Come vediamo dal disegno, la retta £$ t $£ interseca il poligono £$ Q $£ nel punto £$ D $£. In altre parole, possiamo dire che il punto £$ D $£ appartiene alla retta £$ t $£.
l) Disegna e scrivi l’equazione della retta £$ r$£ passante per il lato £$ D’C’ $£.
La retta che passa per il lato £$ D’C’ $£ è una retta orizzontale, quindi è formata da tutti i punti che hanno ordinata uguale a £$ -6 $£. L’equazione della retta £$ r $£ è £$ y = -6$£.
m) Scrivi le coordinate di £$ N $£ punto d’intersezione tra la retta £$t$£ e la retta £$r$£.
Per trovare le coordinate del punto di intersezione tra le due rette £$ t $£ e £$ r $£ non dobbiamo andare a occhio! Si tratta di risolvere un sistema di due equazioni. Lo imparerai presto:
$$ \begin{cases} y = +3x \\ y = -6 \end{cases} $$
Non è niente di difficile: il sistema si traduce in una semplice equazione! Sostituiamo il valore di £$ y $£ indicato dalla retta £$ r $£ nell’equazione della retta £$ t $£ e ricaviamo la £$ x $£:
$$ y = +3x \\ -6 = +3x \\ x = -2 $$
Quindi il punto di intersezione ha coordinate £$ N(-2; -6) $£.
