Esercizi con le quattro operazioni tra monomi
La matematica potremmo definirla come una disciplina che si compone di sfide: una di queste sfide riguarda le quattro operazioni con i monomi, che ad un primo sguardo possono intimorire e non poco! Per questo, nel nostro articolo, abbiamo preparato per te alcuni esercizi che potrai risolvere per fare pratica, ripetere e prepararti alla verifica: potrai stamparli in pdf e verificarne il risultato!
Ma prima di immergerci negli esercizi con i monomi, è essenziale capire cosa sia esattamente un monomio. Un monomio è un’espressione algebrica composta da un coefficiente e una o più variabili alzate a una potenza non negativa. Ad esempio, £$5x^2 , -3yz$£ sono monomi. Comprendere come manipolare e lavorare con questi monomi attraverso le quattro operazioni fondamentali – addizione, sottrazione, moltiplicazione e divisione – è importante per arrivare preparati alla verifica e all’interrogazione. Questo articolo ti guiderà attraverso queste operazioni con i monomi attraverso una serie di esercizi con le quattro operazioni e i monomi che potrai svolgere per affinare le tue abilità.
Esercizi con la somma algebrica e la sottrazione tra monomi

L’addizione tra monomi avviene quando due monomi hanno la stessa parte letterale, cioè le stesse variabili con gli stessi esponenti. In questo caso, sommiamo solo i coefficienti. Per esempio, £$3x^2 + 5x^2 = 8x^2$£. Se i monomi non hanno la stessa parte letterale, la somma algebrica tra monomi non può essere eseguita in termini semplici. Ad esempio, £$3x^2 + 4x$£ resta invariato come somma.
La sottrazione tra monomi segue la stessa logica dell’addizione. Due monomi con la stessa parte letterale possono essere sottratti tra loro sottraendo i loro coefficienti. Ad esempio, £$7x^3 – 3x^3 = 4x^3$£. Se le parti letterali sono diverse, la sottrazione non può essere semplificata e i monomi restano come sono, proprio come nel caso dell’addizione.
Se stai cercando esercizi sulle addizioni e sulle sottrazioni tra monomi, scarica il PDF e allenati!
Elevamento a potenza di monomi
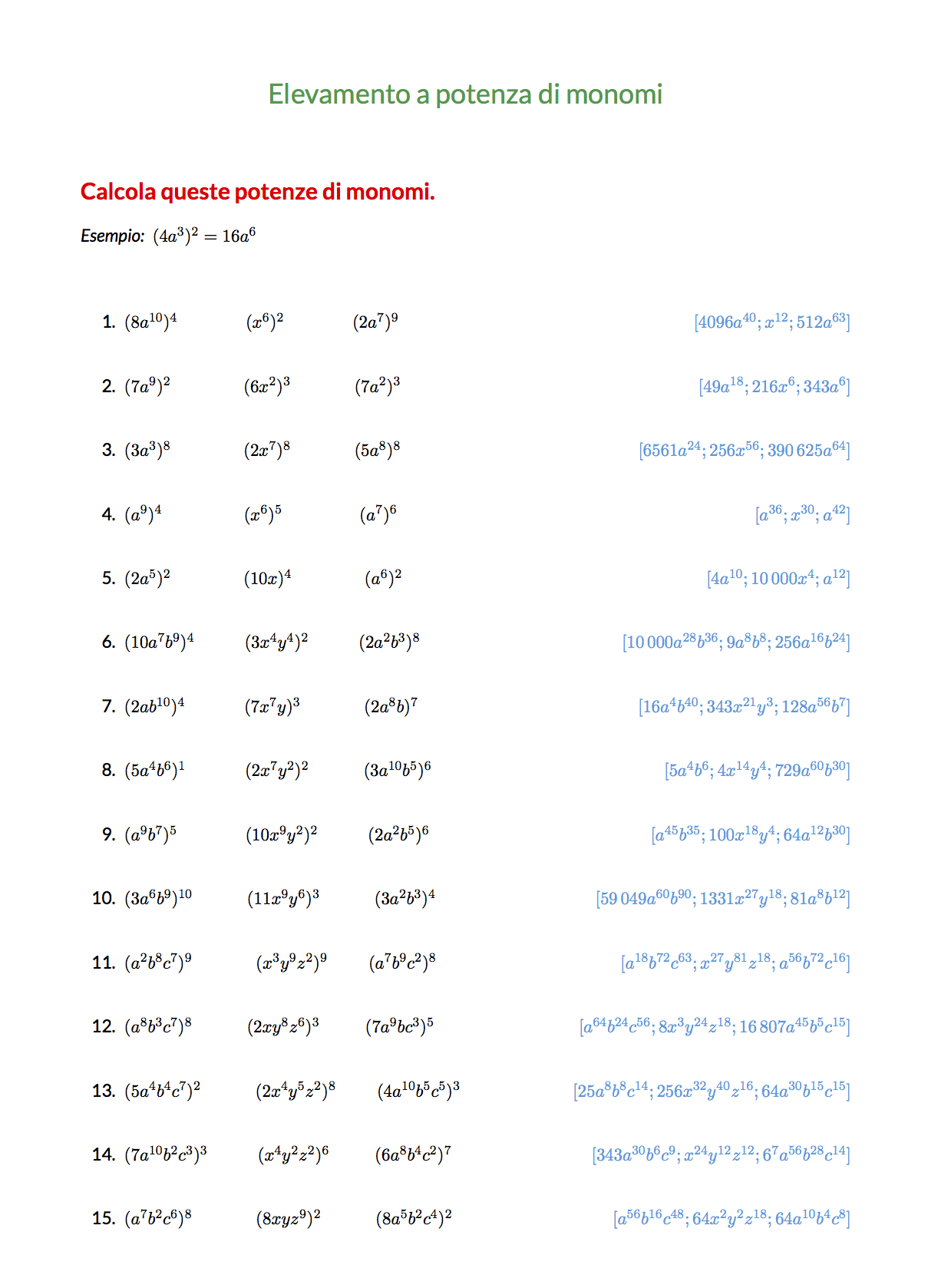
Elevare un monomio a una potenza significa moltiplicare il monomio per se stesso un determinato numero di volte. Durante questo processo, due passaggi principali devono essere seguiti:
- Eleva il coefficiente del monomio alla potenza desiderata. Ad esempio, se stiamo elevando £$2x^2$£ al quadrato, il coefficiente 2 verrà elevato al quadrato, con risultato 4.
- Moltiplica gli esponenti delle variabili per il nuovo esponente. Nell’esempio precedente di £$2x^2$£ elevato al quadrato, l’esponente 2 della variabile x viene moltiplicato per 2 (il nuovo esponente), risultando in £$x^4$£.
Combinando i due passaggi, £$2x^2$£ elevato al quadrato diventa £$4x^4$£. Questo metodo si applica indipendentemente dal numero di variabili presenti nel monomio. È fondamentale ricordare che elevare un monomio a una potenza non modifica la base della variabile, ma solo il suo esponente.
Hai bisogno di esercizi sull’elevamento a potenza di monomi? Scarica il PDF!
Moltiplicazioni tra monomi

Quando si tratta di moltiplicazione tra monomi, moltiplichiamo i coefficienti tra loro e sommiamo gli esponenti delle variabili corrispondenti. Ad esempio, £$2x^2*3x^3=6x^5$£. Se un monomio ha più di una variabile, applichiamo la stessa regola per ciascuna di esse.
Esercizi e soluzioni con le moltiplicazoni tra monomi. Scarica il PDF!
Esercizi con le divisioni tra monomi

La divisione tra monomi richiede che si dividano i coefficienti tra loro e si sottraggano gli esponenti delle variabili corrispondenti. Ad esempio, £$6×4:3x^2=2x^2$£. È essenziale ricordare che la divisione per un monomio con coefficiente zero non è possibile. Inoltre, se la variabile nel denominatore ha un esponente maggiore di quella nel numeratore, la divisione ci darà come risultato una frazione.
Tanti esercizi per allenare le divisioni tra monomi. Scarica il PDF!
