Le operazioni con i monomi: svolgimento
Un monomio, per definizione, è un’espressione algebrica composta da una parte letterale ed una numerica. Pensate ad esempi come £$3x^2, 5ab, 7xy$£. In questi esempi, i numeri 3, 5 e 7 sono i coefficienti, mentre x, y, a e b rappresentano la parte letterale del monomio. La potenza a cui è elevata ogni variabile indica il grado del monomio rispetto a quella variabile.
Sommare, sottrarre, moltiplicare e dividere monomi sono le operazioni fondamentali che esploreremo in questo articolo, imparando come trattare i coefficienti, come gestire le potenze e come riconoscere quando e come si possono combinare monomi simili.
Pronti? Iniziamo!
- La somma algebrica tra monomi
- L'elevamento a potenza di monomi
- La moltiplicazione tra monomi
- La divisione tra monomi
- Espressioni con i monomi
- Sfida sulle operazioni con i monomi
La somma algebrica tra monomi
L’operazione di somma o differenza tra monomi può essere fatta solo se i monomi sono tra loro simili. Cosa vuol dire? Due monomi sono simili se hanno la stessa parte letterale. Quindi la somma o la differenza tra monomi simili dà come risultato un monomio simile a quelli di partenza e avente come coefficiente la somma o la differenza dei coefficienti dei monomi con cui stai facendo l’operazione.
Se in un cestino di frutta metti £$ 2 $£ arance (£$ 2a $£) e poi ancora £$ 4 $£ arance (£$ 4a $£), alla fine avrai £$ 6 $£ arance:
£$ 2a + 4a = (2+4)a = 6a $£
Se nel cestino invece metti £$ 2 $£ arance (£$ 2a $£) e £$ 4 $£ banane (£$ 4b $£) alla fine avrai… £$ 2 $£ arance e £$ 4 $£ banane!
£$ 2a + 4b $£ … rimane £$ 2a + 4b $£
Se due monomi sono simili, cioè hanno la stessa parte letterale, allora il risultato della loro somma algebrica sarà un monomio che ha:
- come coefficiente numerico, la somma dei coefficienti
- come parte letterale, la stessa parte letterale degli addendi
£$ 2a + 4a = (2+4)a = 6a $£
Se i due monomi simili sono anche opposti allora il risultato dell’addizione è [iol_placeholder type="formula" engine="katex" display="inline"/].
£$ -5a + 5a = (-5 + 5)a =0a =0 $£
Se i due monomi non sono simili, non puoi “calcolare" la somma! Facendo la somma tra monomi non simili, troviamo un oggetto più complesso che si chiama polinomio.
£$ 2a + 4b $£ è un polinomio!
L’elevamento a potenza di monomi
Quando hai un monomio elevato ad una certa potenza £$n$£ devi sfruttare la proprietà della potenza di potenza, cioè £$(a^n)^m=a^{n\cdot m}=a^{nm}$£.
Il coefficiente sarà quindi elevato alla £$n$£ e l’esponente di ogni lettera che forma la parte letterale sarà moltiplicato per £$n$£!
Ricordati anche che £$(a^n)^1=a^n$£ e che £$(a^n)^0=1$£!
£$ (2^3)^4 = 2^{3\cdot4}=2^{12}$£
Questa proprietà vale anche per le lettere che formano la parte letterale di un monomio:
£$ (a^5)^2 = a^{5\cdot2} = a^{10}$£
Allora, per calcolare la potenza di un monomio occorre:
-
- elevare a potenza il coefficiente numerico
- elevare a potenza ciascuna lettera che forma la parte letterale
La moltiplicazione tra monomi
Quando vuoi moltiplicare due monomi non devi far altro che moltiplicare tra loro i coefficienti e per la parte letterale moltiplicare le parti letterali di ogni singolo monomio. Attento però a fare quest’ultima operazione nel modo corretto! Devi usare la proprietà delle potenze: il prodotto di due potenze con ugual base dà come risultato un’altra potenza con la stessa base che ha per esponente la somma degli esponenti, cioè £$a^n\cdot a^m=a^{n+m}$£.
Per farlo dobbiamo:
- moltiplicare tra loro i coefficienti numerici
- moltiplicare tra loro le lettere che formano la parte letterale
Anche per le moltiplicazioni ripassiamo bene le proprietà delle potenze, in particolare il prodotto di due potenze con la stessa base, cioè la proprietà che dice:
£$ 3^4\cdot3^3 = 3^{3+4}=3^7 $£
Questa proprietà vale anche per le lettere:
£$ x^2\cdot x^6 = x^{2+6} =x^8 $£
La divisione tra monomi
Non è sempre possibile fare la divisione tra due monomi e ottenere come risultato un monomio. Otterrai un monomio se ogni lettera del monomio divisore compare anche nel monomio dividendo e gli esponenti del monomio divisore sono minori o uguali rispetto a quelli del monomio dividendo. Se questo non accade il quoziente, cioè il risultato della tua divisione, sarà una frazione algebrica (un’espressione algebrica frazionaria).
Per calcolare le divisioni tra polinomi ripassiamo bene la proprietà delle potenze del quoziente tra potenze con la stessa base, cioè la proprietà che dice:
£$ 5^7 : 5^2 = 5^{7-2}=5^5 $£
Questa proprietà vale anche per le lettere:
£$ t^4 : t = t^{4-1} =t^3 $£
Per fare una divisione tra monomi dobbiamo:
- dividere tra loro i coefficienti numerici
- dividere tra loro le lettere che formano la parte letterale
£$ a^3b^2 : 3 ab^2 = (1:3)a^{3-1}b^{2-2}= \frac{1}{3} a^2b^0=\frac{1}{3}a^2$£
Proviamo a fare queste divisioni:
- £$ -6a^2 : 3a^3 = \frac{-6}{3}a^{2-3}=-2a^{-1}$£. Il risultato ha esponente negativo;
- £$ 3ab : 2c = \frac{3}{2} abc^{-1}$£, anche in questo caso l’esponente è negativo.
Questi non sono monomi!
Quando devi calcolare una divisione tra monomi, osserva bene la parte letterale del primo e del secondo monomio.
- Nel secondo monomio ci sono delle lettere che non sono nel primo monomio?
- Nel secondo monomio l’esponente di una lettera è più grande dell’esponente della stessa lettera nel primo monomio?
Se hai risposto sì almeno a una di queste domande, allora i due monomi non sono divisibili.
Espressioni con i monomi
Esercizio svolto facile
Esercizio svolto medio
Esercizio svolto difficile
In questi video troverai delle espressioni svolte con i monomi! Nel primo e nel secondo basterà aver capito come si fanno le operazioni con i monomi, il terzo invece è un pochino più complicato: gli esponenti delle lettere non sono solo numeri ma lettere! Come si svolgono queste espressioni? Se ti ricordi bene le proprietà delle potenze sarà facilissimo risolvere questa espressione!
Cosa potrebbero chiederti nell’interrogazione
Si possono sempre sommare o sottrarre due o più monomi? E un monomio moltiplicato per un altro monomio dà ancora come risultato un monomio? Ecco alcune domande… potrebbero essere quelle della tua interrogazione di domani!
Esercizi sulla somma e differenza

Se stai cercando esercizi sulle addizioni e sulle sottrazioni tra monomi, scarica il PDF e allenati!
Esercizi sull’elevamento a potenza
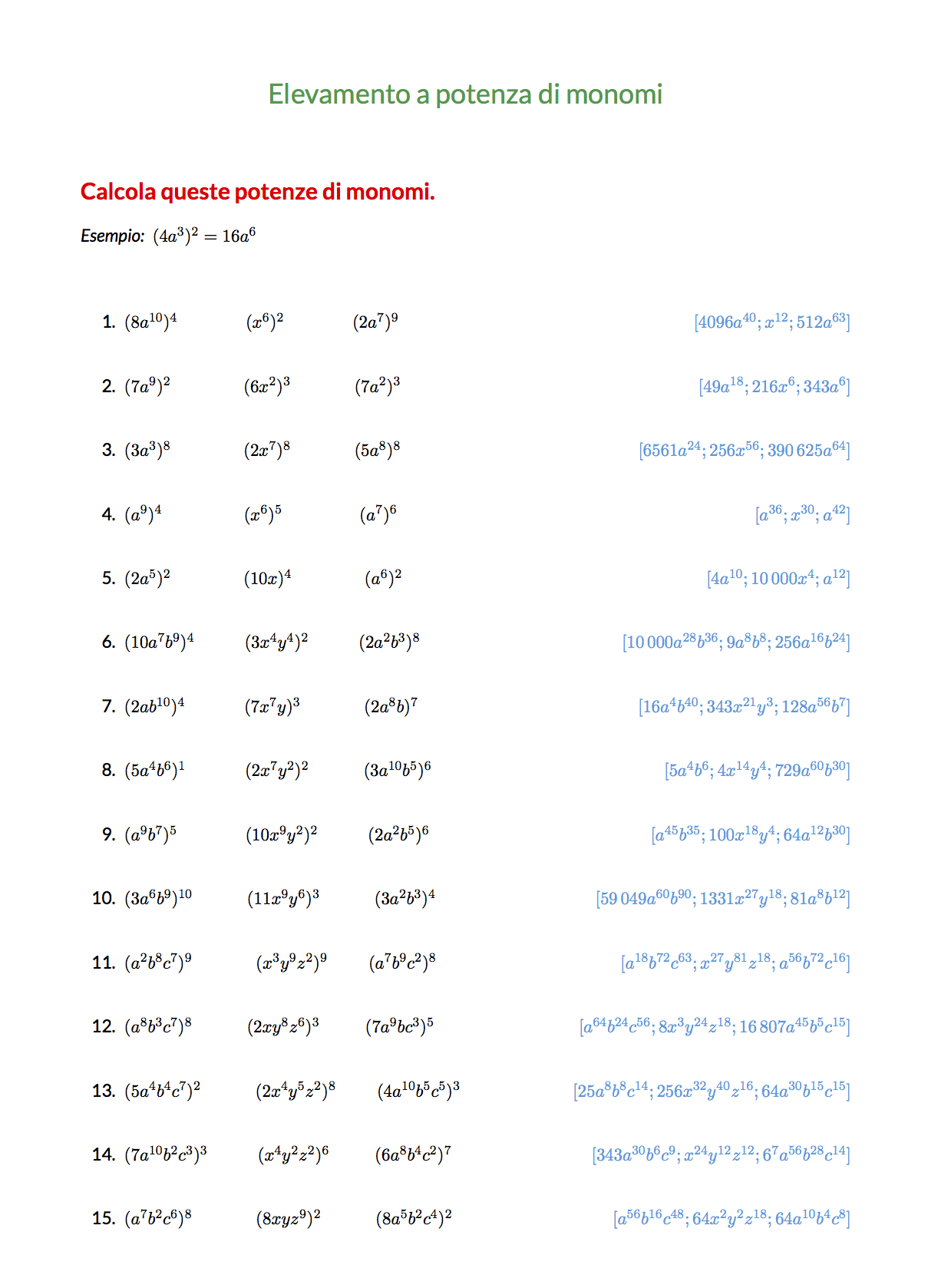
Hai bisogno di esercizi sull’elevamento a potenza di monomi? Scarica il PDF!
Esercizi sulle moltiplicazioni

Esercizi e soluzioni con le moltiplicazoni tra monomi. Scarica il PDF!
Esercizi sulle divisioni

Tanti esercizi per allenare le divisioni tra monomi. Scarica il PDF!
Sfida sulle operazioni con i monomi
Sfida in Africa:
Ecco la soluzione:
Ancora viaggi! Ma stavolta destinazione…Africa! Per arrivare però hai molte tratte da fare, ognuna con un costo diverso. Mettiti alla prova con questa sfida sulle operazioni con i monomi. Guarda i video e fai gli esercizi per diventare un esperto di monomi!
