Operazioni con i polinomi: come risolverle
Le operazioni con i polinomi costituiscono una delle pietre miliari dell’algebra. I polinomi, espressioni algebriche composte da somme e prodotti di variabili e coefficienti, sono strumenti fondamentali utilizzati per descrivere una vasta gamma di fenomeni matematici e reali. La capacità di manipolare e risolvere operazioni con i polinomi è essenziale per avanzare non solo nello studio dell’algebra ma anche in campi applicativi come l’ingegneria, la fisica, l’economia e oltre.
Le operazioni di base con i polinomi includono l’addizione, la sottrazione, la moltiplicazione e, in certi contesti, la divisione. Ognuna di queste operazioni segue regole specifiche che tengono conto della struttura dei polinomi e delle proprietà delle operazioni algebriche.
L’addizione e la sottrazione di polinomi si svolgono combinando termini simili, ovvero termini che hanno la stessa parte variabile elevata agli stessi esponenti. Questo processo richiede attenzione e precisione per garantire che solo i termini effettivamente simili vengano combinati. Il risultato è un nuovo polinomio in cui i coefficienti dei termini simili sono stati sommati o sottratti.
La moltiplicazione di polinomi, d’altra parte, è un’operazione più complessa che implica la distribuzione di ogni termine di un polinomio attraverso ogni termine di un altro. Questo processo, noto come metodo di distribuzione o legge distributiva, richiede che ogni termine del primo polinomio sia moltiplicato per ogni termine del secondo, seguito dalla combinazione di termini simili nel prodotto risultante.
Infine, vedremo la divisione tra polinomi: è un’operazione che consente di dividere un polinomio, detto dividendo, per un altro polinomio, detto divisore, ottenendo un quoziente e, in alcuni casi, un resto. Il processo è simile alla divisione tra numeri interi, ma con alcune specificità dovute alla natura dei polinomi.
Scopriamo insieme come si svolgono.
Ripasso di grado e forma normale di polinomi
Alcuni esercizi per iniziare su come ridurre i polinomi in forma normale e calcolarne il grado. Scarica subito il PDF!
Come calcolare l’addizione tra polinomi
Come calcolare l’addizione tra polinomi? Anche con i polinomi possiamo fare tutte le operazioni che abbiamo visto con i monomi.
Come facciamo a sommare due polinomi? Per fare l’addizione tra due polinomi, basta scrivere il segno £$ + $£ tra uno e l’altro.
Ricordati di usare le parentesi! Con il segno £$ + $£, puoi togliere la parentesi mantenendo invariati i segni dei monomi.
Quello che otteniamo è ancora un polinomio! Dobbiamo ridurlo a forma normale… Quindi cerchiamo i monomi simili e sommiamoli!
Esercizi sulla somma tra polinomi
Esercitati con le addizioni tra i polinomi. Scarica i PDF per prepararti alle prossime verifiche!
Sottrazione tra due polinomi
Come si fa, invece, a sottrarre due polinomi?
Per fare la sottrazione tra due polinomi, scriviamo il segno £$ – $£ tra uno e l’altro, ricordandoci di mettere i due polinomi tra parentesi.
Per togliere le parentesi, ricordiamoci di cambiare tutti i segni dei monomi che compongono il secondo polinomio, perché era preceduto dal segno £$ – $£.
Otteniamo ancora un polinomio! Possiamo procedere come per la somma riducendo il risultato a forma normale.
Guarda il video per vedere un esempio!
Esercizi sulla sottrazione tra polinomi
Esercitati con le sottrazioni tra i polinomi. Scarica i PDF per prepararti alle prossime verifiche!
Moltiplicazione tra polinomi
E infine come si fa la moltiplicazione tra due polinomi?
Dobbiamo ancora una volta utilizzare la proprietà distributiva, ma più di una volta! Sfruttiamo la proprietà distributiva per ogni monomio che compone uno dei due polinomi.
Distribuiamo ogni monomio che compone il primo polinomio sul secondo polinomio, in modo da moltiplicare tra loro tutti i pezzetti di ciascun polinomio.
Attenzione a non dimenticarne neanche uno!
Moltiplicazione tra un monomio e un polinomio
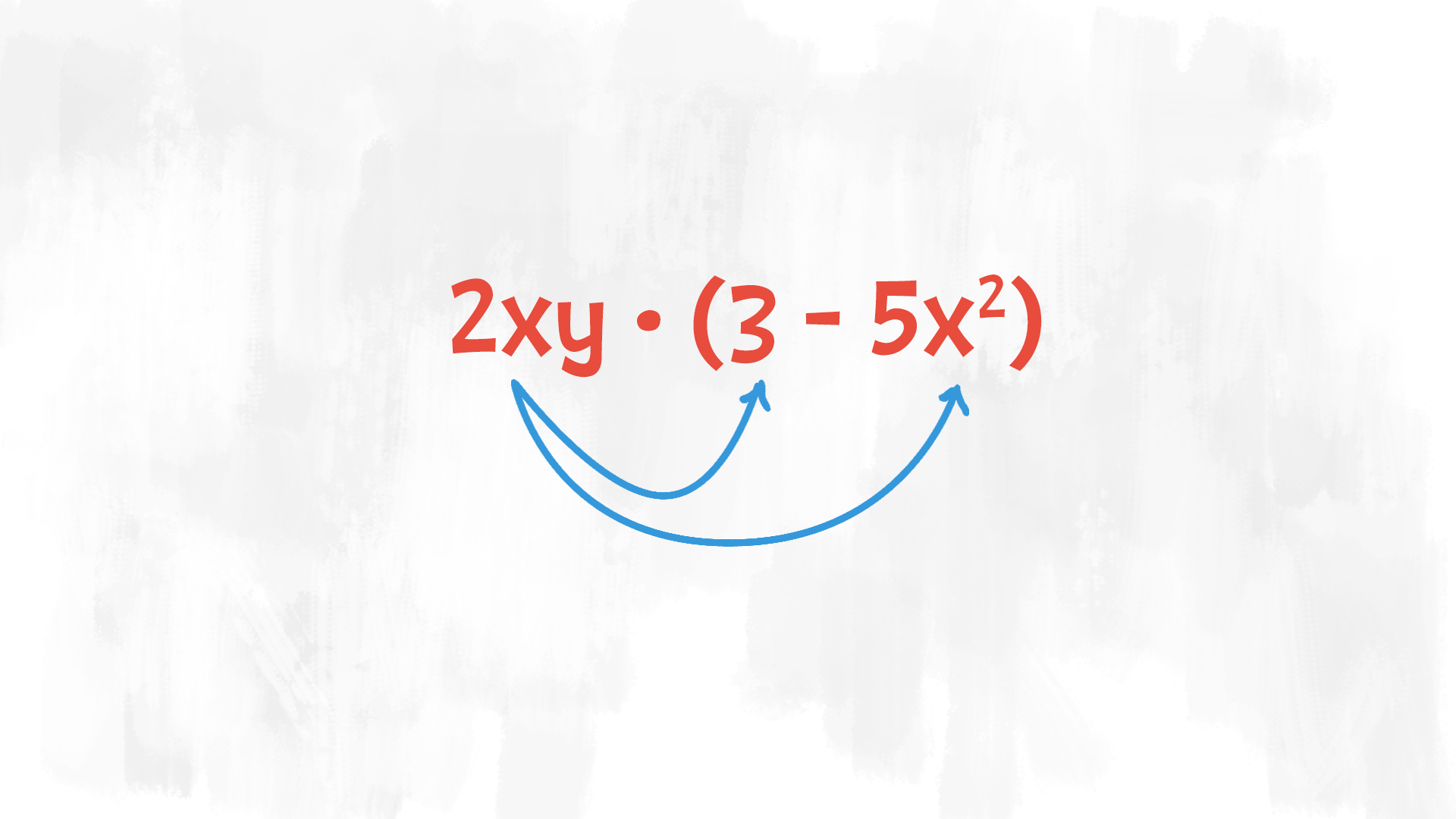
Iniziamo moltiplicando un monomio per un polinomio.
£$ 2xy \cdot (3 – 5x^2) $£
Utilizziamo la proprietà distributiva della moltiplicazione rispetto alla somma. La ricordi?
£$ 2 \cdot (3 + 5) = 2\cdot3 + 2\cdot 5$£
Allora “distribuiamo" il monomio su ciascun monomio del polinomio.
£$ (2xy \cdot 3) + (2xy\cdot(-5x^2)) $£
Eseguiamo la moltiplicazione tra monomi:
£$ (2\cdot3)xy + (2\cdot(-5)xyx^2) = \\ = 6xy – 10x^3y $£
Esercizi sulla moltiplicazione tra polinomi
Svolgi le moltiplicazioni tra polinomi e preparati alla verifica al meglio!
Scarica il PDF degli esercizi:
Divisione tra polinomi
Come fare la divisione tra due polinomi? Puoi sempre fare la divisone tra due polinomi? In questo video risolveremo tutti questi problemi!
La divisione tra il polinomio £$A$£ e il polinomio £$B$£ (£$A$£ di grado £$\ge B$£) è sempre possibile, perché esiste sempre un polinomio £$Q$£ e (eventualmente) un (polinomio) resto £$R$£ tali che £$ B\cdot Q + R = A $£
Divisione di un polinomio per un monomio
Come si fa la divisione tra un polinomio e un monomio? È sempre possibile farla?
Un polinomio è divisibile per un monomio se ogni termine del polinomio è divisibile per il monomio.
Puoi anche dire che un polinomio £$A$£ (dividendo) è divisibile per un monomio £$B$£ (divisore) se esiste un polinomio £$Q$£ che moltiplicato per £$B$£ dà come risultato £$A$£.
Interrogazione sulle operazioni tra polinomi
Ti senti pronto per l’interrogazione? Misura la tua preparazione sulle operazioni tra polinomi con queste brevi domande! Hai risposto correttamente? Allora domani non avrai problemi!
Sfida sulle operazioni tra polinomi
Mettiti alla prova:
Soluzione alla sfida:
Hai completato la progettazione del viaggio in Africa! Quale polinomio rappresenta il costo totale del viaggio? La sfida è sulle operazioni con i polinomi! Qualcosa non ti è chiaro? Guarda i video ed allenati con gli esercizi!