I numeri relativi e le loro proprietà
I numeri relativi sono un concetto fondamentale che estende l’idea dei numeri naturali (come 1, 2, 3, …) includendo anche i numeri negativi (come -1, -2, -3, …), nonché lo zero. Questi numeri permettono di descrivere situazioni che non sarebbero rappresentabili utilizzando solo numeri naturali o interi positivi.
Per affrontare al meglio compiti in classe, verifiche e interrogazioni, è importante padroneggiare il concetto di numero relativo e quali sono le proprietà che li contraddistinguono. Scopriamole insieme!
Ripassa le proprietà dei numeri relativi e allenati con le operazioni e le potenze. Impara a calcolare le somme algebriche, le moltiplicazioni, le divisioni e le potenze di numeri relativi.
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Numeri sotto e sopra la terra: i numeri relativi
- La rappresentazione dei numeri relativi
- L'insieme dei numeri interi e altri insiemi numerici
- Numeri relativi concordi, discordi, opposti e valore assoluto
Numeri sotto e sopra la terra: i numeri relativi
Che cosa sono i numeri relativi?
I numeri relativi sono quei numeri che hanno il segno, positivo o negativo. Finora abbiamo studiato i numeri naturali, le frazioni, le radici: tutti numeri senza segno.
I numeri naturali con l’aggiunta del segno £$ + $£ o del segno £$ – $£ costituiscono l’insieme dei numeri interi che indichiamo con £$ \mathbb{Z} $£.
Lo chiamiamo insieme dei numeri interi perché contiene tutti i numeri “interi": non contiene frazioni, né decimali, né radici.
Anche lo 0 è un numero relativo, ma non è né negativo, né positivo!
La rappresentazione dei numeri relativi
A che cosa servono questi numeri relativi? Non bastano i numeri naturali, le frazioni e le radici?
Abbiamo visto che tra numeri naturali non è sempre possibile fare la sottrazione. Per questo motivo abbiamo introdotto l’insieme dei numeri interi £$ \mathbb{Z} $£: in questo insieme possiamo svolgere tutte le addizioni e tutte le sottrazioni.
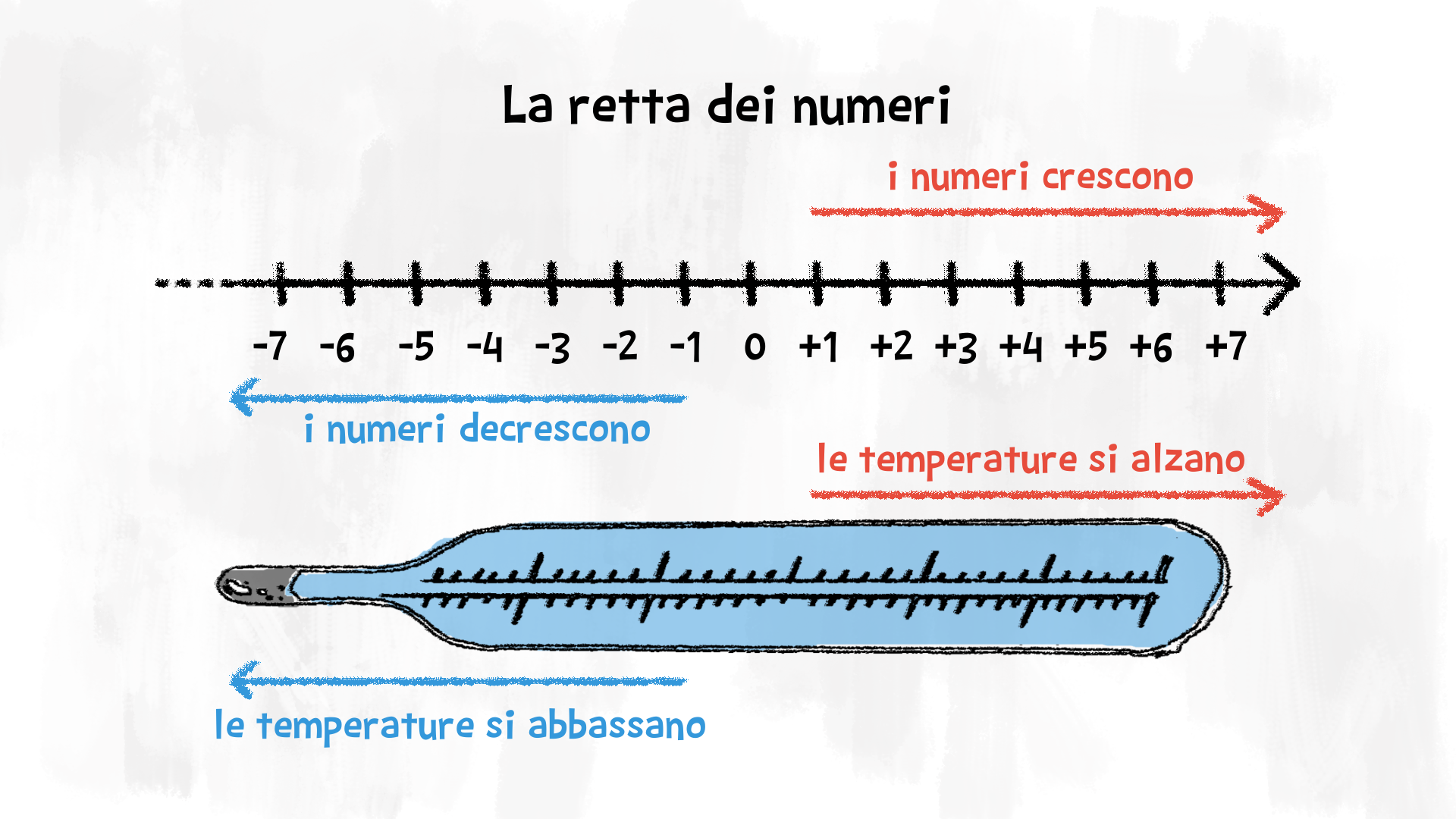
Per studiare i numeri interi ci aiutiamo con la retta numerica: lo £$ 0 $£ è come uno specchio. Alla sua destra ci sono i numeri positivi che crescono sempre di più, alla sua sinistra i numeri specchiandosi diventano negativi e decrescono sempre di più.
Esempio: qual è il numero più grande tra £$ – 5 $£ e £$ – 12 $£?
Non farti ingannare! I numeri con il segno meno funzionano al contrario: possiamo dire che “più sono grandi, più sono piccoli". Quindi £$ -5 > -12 $£.
Non ne sei convinto? Prova a immaginare se fa più freddo con £$ -5^\circ \text{C} $£ o con £$ -12^\circ \text{C} $£… 😉
L’insieme dei numeri interi e altri insiemi numerici
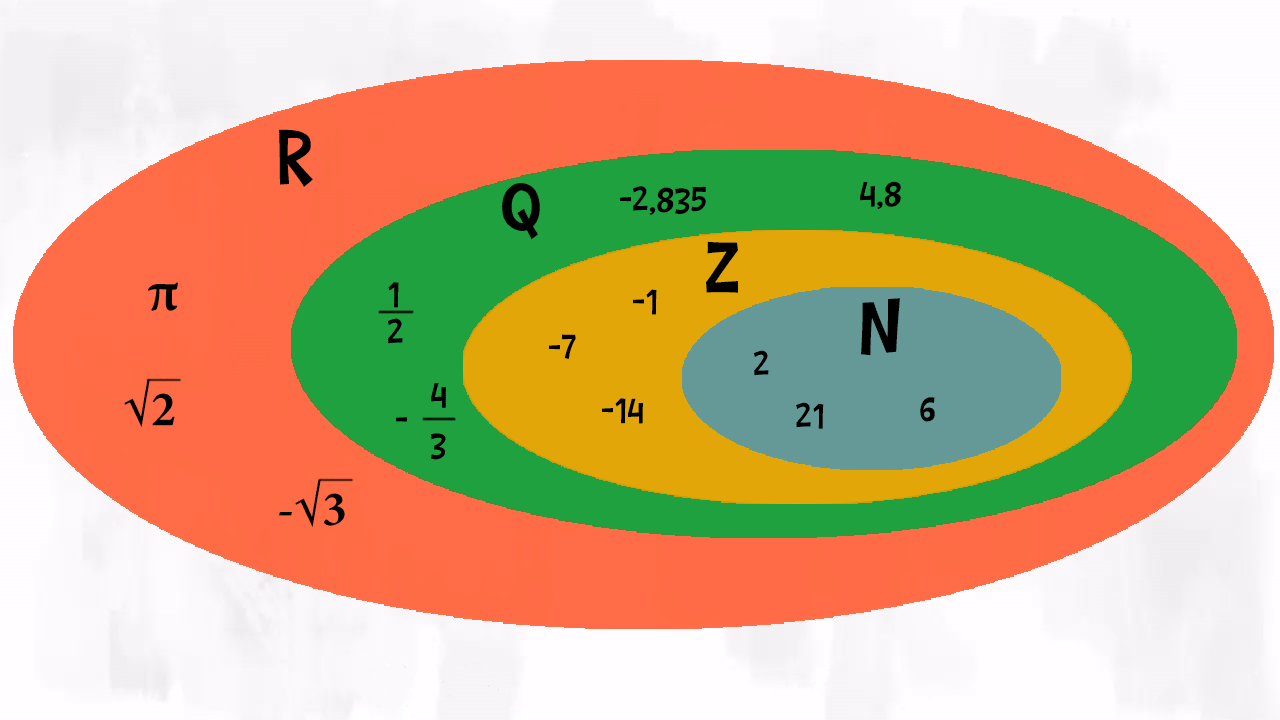
L’insieme dei numeri relativi, o numeri interi, è indicato con la lettera £$ \mathbb{Z} $£.
Contiene tutti i numeri interi, positivi e negativi. Quindi l’insieme dei numeri naturali £$ \mathbb{N} $£ è un suo sottoinsieme.
Quali altri numeri conosci?
Abbiamo studiato anche le frazioni, cioè i numeri razionali: sono i numeri dell’insieme £$ \mathbb{Q} $£.
I numeri razionali possono essere positivi e negativi, quindi possiamo scrivere che £$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} $£.
Ci sono però altri numeri che non si possono scrivere sotto forma di frazione, come £$ \pi $£ oppure £$ \sqrt 2 $£: sono i numeri irrazionali! Fanno parte dell’insieme dei numeri reali £$ \mathbb{R} $£. Anche i numeri irrazionali possono essere positivi o negativi!
Quindi gli insiemi numerici sono
$$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} $$
Numeri relativi concordi, discordi, opposti e valore assoluto
Due numeri che hanno lo stesso segno vanno d’accordo: sono concordi!
Due numeri che hanno segno diverso non vanno d’accordo: sono discordi!
Esempi:
£$ -12 $£ e £$ -4 $£ sono concordi, hanno entrambi segno £$ – $£.
£$ -1 $£ e £$ +6 $£ sono discordi, hanno segno diverso!
Mettiamoci sullo £$ 0 $£ della retta dei numeri, facciamo £$ 8 $£ salti verso destra e raggiungiamo il numero £$ +8 $£. Se facciamo £$ 8 $£ salti verso sinistra torniamo esattamente al nostro punto di partenza, lo £$ 0 $£.
Possiamo rappresentare l’operazione appena fatta con il linguaggio matematico scrivendo £$ +8 + (-8)=0$£.
£$ +8 $£ e £$ -8 $£ sono due numeri discordi la cui somma fa £$ 0 $£: allora sono opposti!
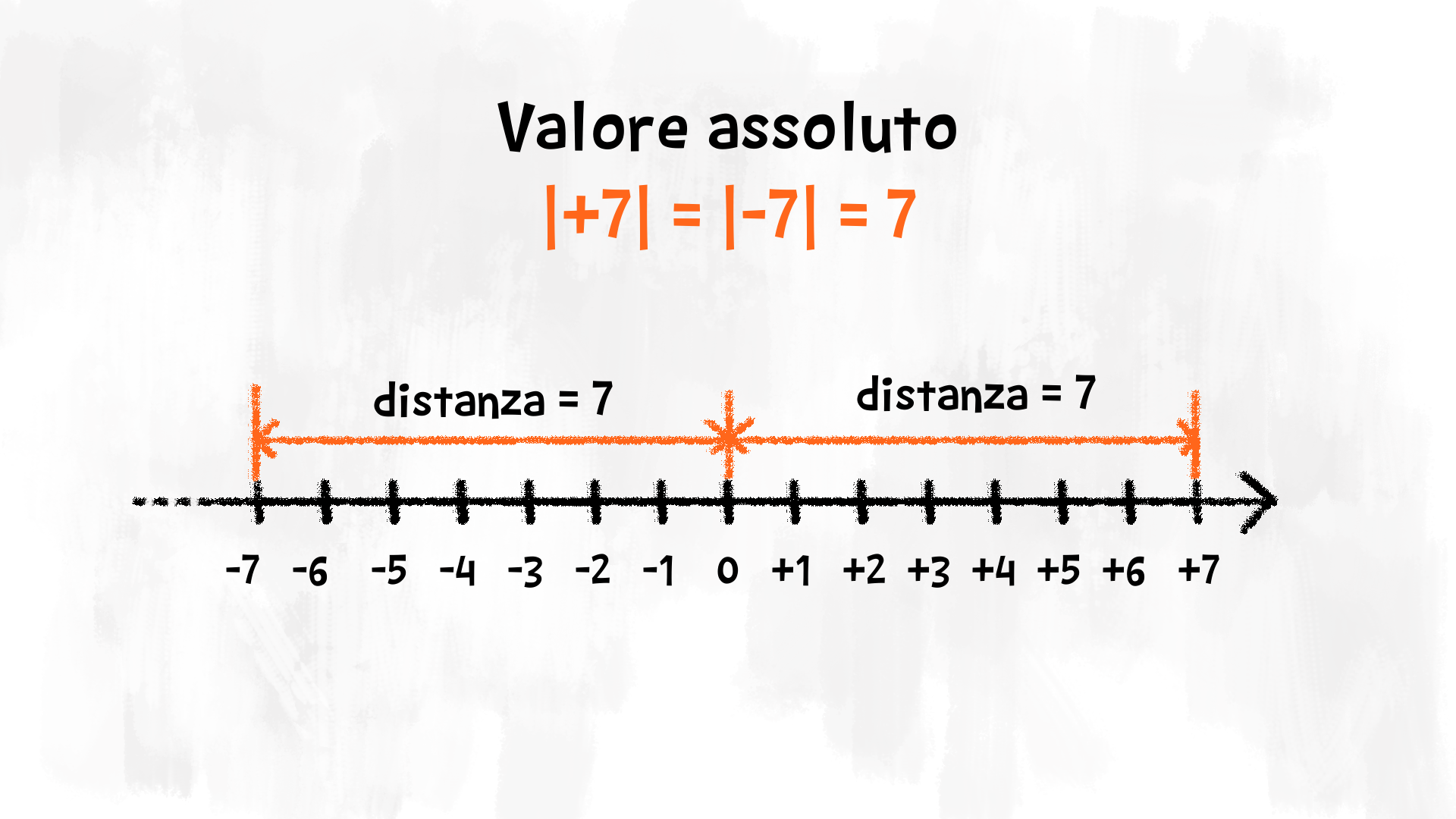
Se rappresentiamo i numeri £$ +8 $£ e £$ -8 $£ sulla retta, notiamo subito che
sono simmetrici rispetto allo £$ 0 $£ e che quindi la loro distanza dallo £$ 0 $£ è la stessa: £$ 8 $£.
Questa distanza si chiama anche valore assoluto o modulo.
Il valore assoluto di £$ +8 $£ e il valore assoluto di £$ -8 $£ sono uguali e valgono £$ 8 $£.
In simboli matematici scriviamo che:
£$ |+8|=|-8| = 8 $£
E il valore assoluto di £$ 0 $£? È £$ 0$£!
£$|0|=0$£
