Numeri primi: come fare la scomposizione in fattori
La scomposizione in fattori primi è un processo matematico che permette di esprimere un numero naturale come un prodotto di numeri primi. I numeri primi sono quei numeri maggiori di 1 che hanno solo due divisori: 1 e loro stessi. La scomposizione in fattori primi è unica per ogni numero ed è molto più che un semplice esercizio matematico. Ad esempio, è estremamente utile nella semplificazione delle frazioni, dove scomponendo numeratore e denominatore in fattori primi, possiamo facilmente cancellare i fattori comuni. Questo processo aiuta anche nel calcolo del minimo comune multiplo e del massimo comune divisore, due concetti fondamentali nelle operazioni con le frazioni e nella risoluzione di vari problemi di algebra.
La scomposizione in fattori primi gioca anche un ruolo significativo nella comprensione delle proprietà dei numeri, come la divisibilità e la struttura dei numeri interi. Scopriamo insieme come fare questa scomposizione!
Numeri primi e numeri composti: la differenza
Un semplice trucco per riconoscerli
Dividi in gruppi e trova i numeri composti
Sentiamo spesso parlare dei numeri primi, ogni tanto se ne scopre qualcuno nuovo… Il più grande numero primo conosciuto ha più di 22 milioni di cifre. Ma cos’è un numero primo? Non si tratta certo del vincitore di una gara di velocità tra numeri… 😉
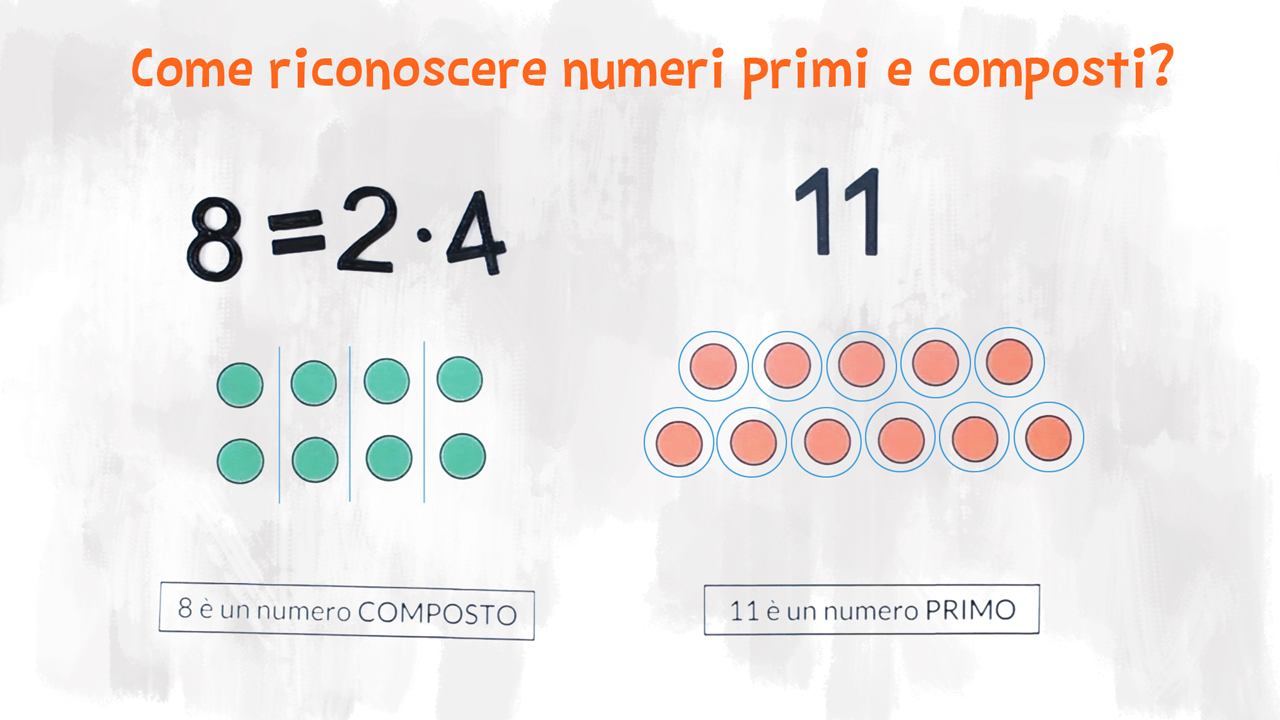
Un numero primo è un numero maggiore di 1 divisibile solo per 1 e per se stesso. Quindi un numero primo è un numero che ha esattamente due divisori.
- 2 è un numero primo: è divisibile solo per 1 e per 2;
- 5 è un numero primo: è divisibile solo per 1 e per 5;
- 17 è un numero primo: è divisibile solo per 1 e per 17;
- …
Ci sono infiniti numeri primi! Lo aveva dimostrato già Euclide nel suo libro Elementi, la più importante opera di matematica che conosciamo, scritto tra il IV e il III secolo a.C.. Ma non tutti i numeri sono primi. Abbiamo parlato di numeri con più divisori diversi oltre all’1 e a loro stessi. Questi numeri con tanti divisori sono i numeri composti, cioè quei numeri che hanno più di due divisori.
Esempio: il 6 è un numero composto perché ha come divisori 1 e 6, ma anche 2 e 3. In tutto ha quattro divisori!
Ma a cosa servono i numeri primi? I numeri primi sono il fondamento della matematica: il teorema fondamentale dell’aritmetica assicura che ogni numero naturale, o è primo, o si può scrivere come prodotto di numeri primi in modo unico. Quindi tra tutti gli infiniti numeri che conosciamo, possiamo riconoscere numeri primi e numeri che sono prodotto di primi!
Scomposizione in fattori dei numeri primi
Scomposizione in fattori
Scomposizione in fattori primi
I numeri sono infiniti, ma non tutti i numeri sono primi… Ci sono infiniti numeri composti, cioè che hanno più di due divisori. Come facciamo a trovare tutti i divisori di un numero composto? Basta scomporlo!
La scomposizione in fattori consiste nel riscrivere il numero di partenza come prodotto di numeri.
Esempio: possiamo scomporre un numero come prodotto di due numeri: £$ 16 = 8 \cdot 2 $£.
Ma è ancora meglio se riusciamo a scomporre un numero in fattori primi. Perché? Ogni numero composto ha una sua scomposizione in fattori primi. Quella scomposizione è unica: nessun altro numero composto può essere scritto come prodotto degli stessi numeri primi elevati agli stessi esponenti.
Esempio: scomponiamo il £$ 16 $£ come prodotto di fattori primi. Possiamo farlo per gradi, quindi £$ 16 = 8 \cdot 2 = 4 \cdot 2 \cdot 2 = 2 \cdot 2 \cdot 2 \cdot 2 = 2^4 $£.
Ma perché dobbiamo metterci a fare tutte queste divisioni per fattorizzare un numero? Potrà esserci utile per risolvere più facilmente i problemi di matematica, per esempio per semplificare le frazioni! Una volta che abbiamo scomposto un numero in fattori primi, non possiamo andare oltre perché abbiamo raggiunto la base dell’aritmetica: possiamo dire che i numeri primi sono un po’ come i quark della fisica. 😉
Ma in pratica, come facciamo a scomporre un numero in fattori primi? Ci sono due tecniche: i diagrammi ad albero oppure una tabella verticale. Vediamoli entrambi scomponendo il numero £$ 24 $£.
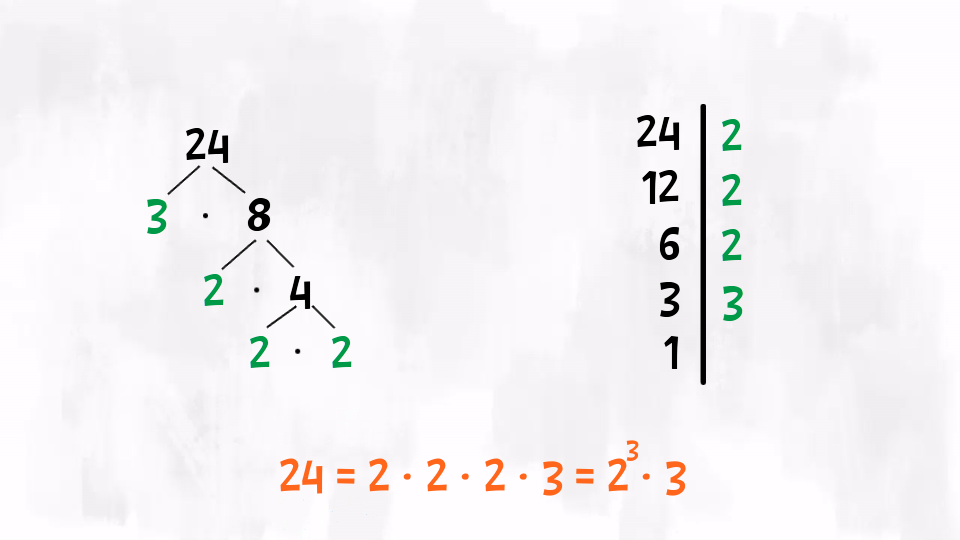
Cosa abbiamo fatto? Nel grafo ad albero, abbiamo ricordato le tabelline: £$ 24 =3 \cdot 8 $£, quindi abbiamo proseguito la scomposizione fino ad ottenere solo numeri primi agli estremi del grafo. Nell’altro caso, invece, visto che il £$ 24 $£ è un numero pari, abbiamo iniziato dividendo per £$ 2 $£ per poi passare al £$ 3 $£ nell’ultimo passaggio. Entrambi i procedimenti si fermano quando arriviamo ad ottenere £$ 1 $£ dalle divisioni successive.
In ogni caso, abbiamo scomposto il £$ 24 $£ in numeri primi! Possiamo raggruppare i numeri primi scrivendo un esponente invece di scrivere le moltiplicazioni per esteso, cioè £$ 24 = 2^3 \cdot 3 $£. Questa scomposizione identifica solo e soltanto il numero £$ 24 $£, nessun altro numero si scompone nello stesso modo.
Come riconoscere un numero primo
Tavola dei numeri primi da 1 a 1000
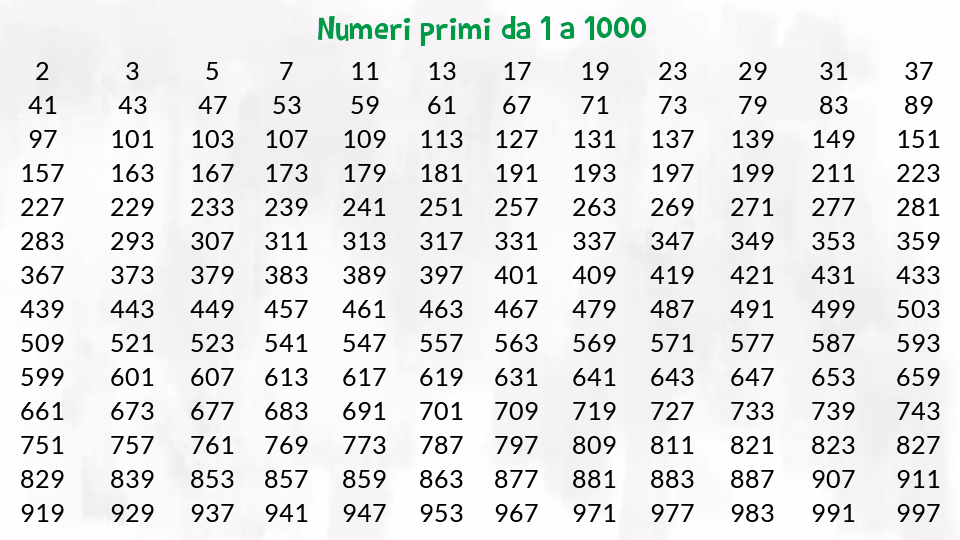
Crivello di Eratostene
Finché ci troviamo davanti numeri relativamente piccoli, non è difficile capire se si tratta di un numero primo o di un numero composto. Cosa succede se i numeri diventano più grandi? Come facciamo ad individuare i divisori di quel numero, o a capire che non ha nessun divisore?
Altrimenti possiamo procedere per tentativi: dividiamo un numero per i primi 2, 3, 5, 7, …. Se troviamo un quoziente esatto, il nostro numero di partenza non è primo, altrimenti andiamo avanti e continuiamo a ricercare divisori tra tutti i numeri primi minori o uguali alla metà del nostro numero. Se non ne troviamo neanche uno che dà un quoziente esatto, abbiamo trovato un numero primo!
In fondo al tuo libro dovrebbe esserci la tabella dei numeri primi da 1 a 1000. Puoi sempre cercare i numeri primi su quella tavola! 😉
Curiosità sui numeri primi e la scomposizione in fattori
Da questa lezione abbiamo imparato molto sui numeri primi… Ma qual è il “primo numero primo"?
Iniziamo dall’inizio. Lo 0 è un numero primo? Abbiamo visto nella scorsa lezione che lo 0 è multiplo di tutti i numeri. Qualsiasi numero moltiplicato per 0, dà come risultato ancora 0. Sicuramente lo 0 non è un numero primo.
Che cosa possiamo dire del numero 1? Anche l’1 non è un numero primo: un numero primo è divisibile per 1 e per se stesso, invece il numero 1 è divisibile solo per se stesso. Non ha due divisori come tutti i numeri primi, ma ne ha uno soltanto: quindi il numero 1 non è un numero primo. E non è neanche un numero composto, avendo un solo divisore: per esserlo, dovrebbe averne più di due!
Il primo numero primo, quindi, è il 2: l’unico primo pari. Tutti gli altri numeri primi sono dispari!
I numeri primi gemelli sono numeri primi consecutivi, cioè separati solo da un numero: per esempio 11 e 13 sono primi gemelli, ma anche 29 e 31, oppure 101 e 103. Nel libro “La solitudine dei numeri primi" si fa un accenno ai numeri primi gemelli: i due protagonisti hanno molte cose in comune, ma non riescono mai a trovarsi perché divisi da un ostacolo insormontabile, un po’ come due primi gemelli che arrivano ad essere molto vicini, ma non riescono mai a toccarsi perché c’è sempre un numero pari ad ostacolarli.
Il più grande numero primo conosciuto ha più di 22 milioni di cifre. Ma perché continuiamo a cercare numeri primi? A cosa servono? Abbiamo già detto che sono la base dell’aritmetica… Bene, quindi? Pensiamo al digitale terrestre, ai sistemi di pagamento elettronico, al biglietto aereo…
In tutte queste cose interviene la crittografia, che significa “scrittura nascosta". La crittografia studia i metodi per rendere il significato di un messaggio incomprensibile a persone non autorizzate a leggerlo. I numeri primi permettono di “cifrare", cioè camuffare un messaggio e poi di decifrarlo, cioè di ritrovarne il significato nascosto!
Per questo continuiamo a scoprirne sempre di più grandi: più grandi sono, più incomprensibili risultano!
È stato istituito un premio per chi riesce a scoprire un numero primo: 3000 dollari, ma si può arrivare fino a 50 mila se si scopre un numero primo con 100 milioni di cifre! Ti è venuta voglia di scoprire un numero primo?
Esercizi sulla scomposizione in fattori
La scomposizione in fattori primi ti preoccupa? Preparati alla verifica di matematica con questi esercizi sulla scomposizione in numeri primi e impara a utilizzarla per semplificare i calcoli.
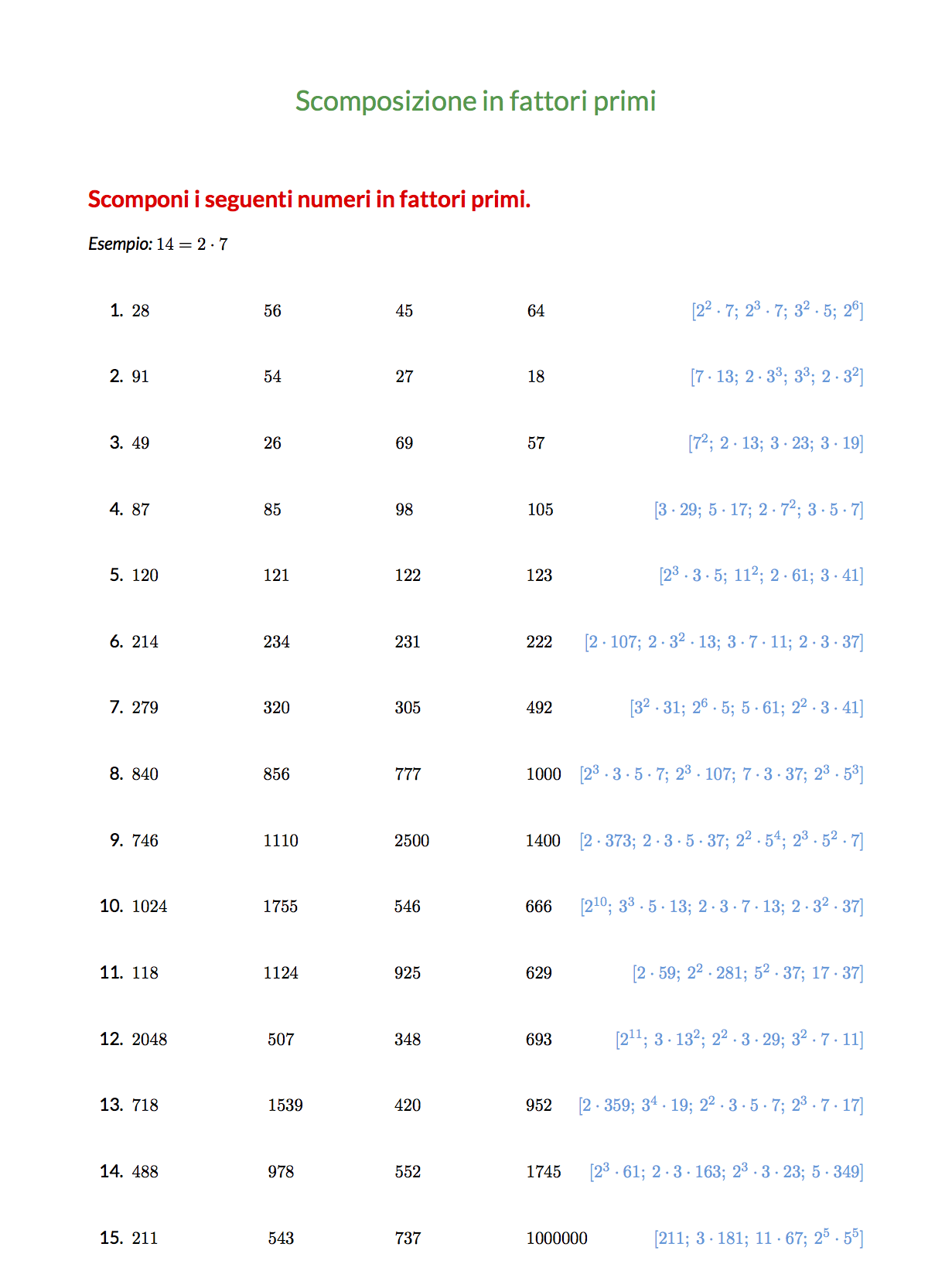
Scarica qui i due pdf con gli esercizi: