Come calcolare le potenze di numeri relativi
I numeri relativi e le potenze giocano un ruolo fondamentale nel mondo della matematica, ma spesso possono sembrare preoccupanti. Sia che si tratti di risolvere equazioni o di gestire complesse operazioni matematiche, la comprensione di come calcolare le potenze dei numeri relativi può fare una grande differenza.
In questo articolo, ci concentreremo su come calcolare le potenze dei numeri relativi e cercheremo di spiegare questo concetto in modo semplice e comprensibile, con tanti esempi pratici!
- Cosa sono le potenze e i numeri relativi
- Potenze di numeri interi e razionali
- Le potenze di numeri relativi con le frazioni
- Potenze con esponente negativo: come si calcolano
- Proprietà delle potenze di numeri relativi
- Interrogazione sulle potenze di numeri relativi interi
- Numeri relativi: vai con la sfida!
Cosa sono le potenze e i numeri relativi
Prima di entrare nel dettaglio di come calcolare le potenze dei numeri relativi, è utile fare un rapido ripasso di cosa sono esattamente questi due elementi.
I numeri relativi includono sia i numeri positivi che i negativi, nonché lo zero. Sono chiamati ‘relativi’ perché il loro valore può essere determinato solo in relazione a un altro numero. Ad esempio, il numero -3 è inferiore a 0 e superiore a -4.
Le potenze, d’altra parte, sono un modo per esprimere il prodotto di un numero moltiplicato per se stesso un certo numero di volte. Il numero che viene moltiplicato è chiamato ‘base’, mentre il numero di volte che viene moltiplicato è chiamato ‘esponente’. Ad esempio, in £$2^3$£, 2 è la base e 3 è l’esponente, il che significa che 2 deve essere moltiplicato per se stesso 3 volte ($$2*2*2$$), dando come risultato 8.
Quando parliamo di calcolare le potenze dei numeri relativi, stiamo combinando questi due concetti. L’operazione diventa un po’ più complicata quando la base è un numero negativo e l’esponente è un numero dispari, rispetto a quando l’esponente è un numero pari. Questo perché una potenza di un numero negativo con esponente dispari dà come risultato un numero negativo, mentre una potenza di un numero negativo con esponente pari dà come risultato un numero positivo. Ad esempio, £$(-2)^3= -8$£ mentre £$(-2)^2 = 4$£.
Nell’articolo, esploreremo in dettaglio come gestire questi casi e altri aspetti delle potenze dei numeri relativi. Vediamoli insieme!
Potenze di numeri interi e razionali
Le potenze di numeri interi potrebbero trarre in inganno… ma basta conoscere un semplice trucchetto per calcolarle in quattro e quattr’otto.
Ricordiamo la definizione di potenza. Ad esempio, fare £$ (+5)^2 $£ vuol dire moltiplicare il numero intero £$ +5 $£ per se stesso £$ 2 $£ volte.
£$ (+5)^2 =(+5)\cdot(+5)=+25$£
Nello stesso modo, fare £$ (-5)^2 $£ vuol dire moltiplicare il numero intero £$ -5 $£ per se stesso £$ 2 $£ volte.
£$ (-5)^2 =(-5)\cdot(-5)=+5^2=+25$£
Il prodotto di due segni £$ – $£ è un segno £$ + $£! Il quadrato di £$ -5 $£ è il numero positivo £$ 25 $£.
E £$ (-2)^3 $£? £$ (-2)^3 = (-2)\cdot(-2)\cdot(-2) = -2^3 = -8$£
Il prodotto di tre segni £$ – $£ è un segno £$ – $£!
In generale, quando calcoliamo la potenza di un numero negativo:
- se l’esponente è pari, il risultato è positivo (segno £$ + $£);
- se l’esponente è dispari, il risultato è negativo (segno £$ – $£).
Perché? Sempre per la regola del segno. Infatti £$–$£ per £$–$£ fa £$+$£ quindi se moltiplichiamo un £$–$£ un numero pari di volte avremmo un £$+$£, se invece lo moltiplichiamo un numero dispari di volte, rimane il £$–$£
Le potenze di numeri relativi con le frazioni
Esempi:
£$ \left(-\frac{2}{5}\right)^2 = \left(-\frac{2}{5}\right) \cdot \left(-\frac{2}{5}\right) = +\frac{4}{25} $£ £$ \left(-\frac{1}{3}\right)^3 = \left(-\frac{1}{3}\right) \cdot \left(-\frac{1}{3}\right) \cdot \left(-\frac{1}{3}\right) = -\frac{1}{27} $£
Ricorda!
Qualsiasi numero elevato alla £$ 1 $£ dà come risultato il numero stesso: £$(-5)^1=-5$£
Qualsiasi numero diverso da £$ 0 $£ elevato alla £$ 0 $£ dà come risultato £$ 1 $£ indipendentemente dal segno: £$(-5)^0=1$£
Potenze con esponente negativo: come si calcolano
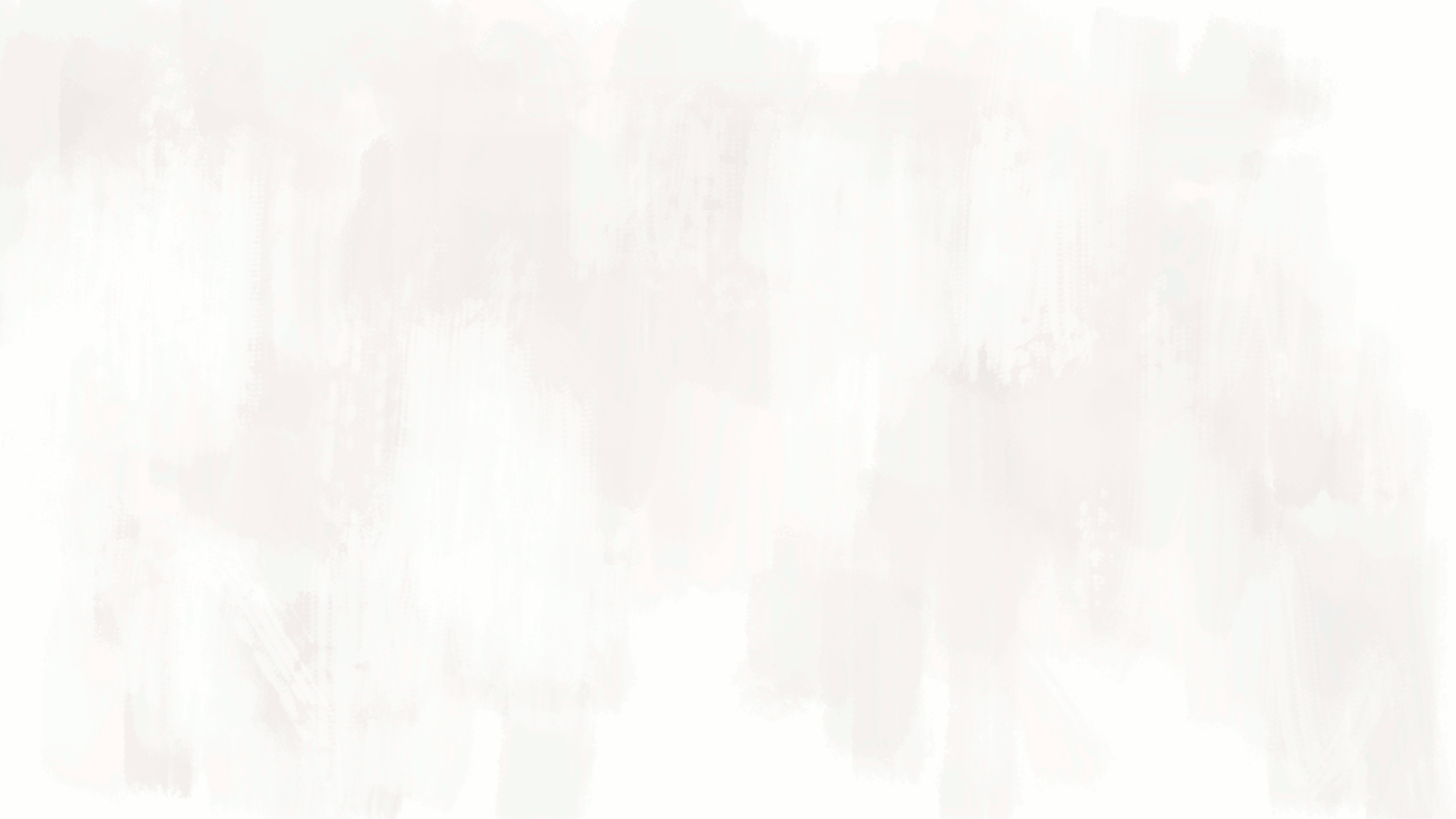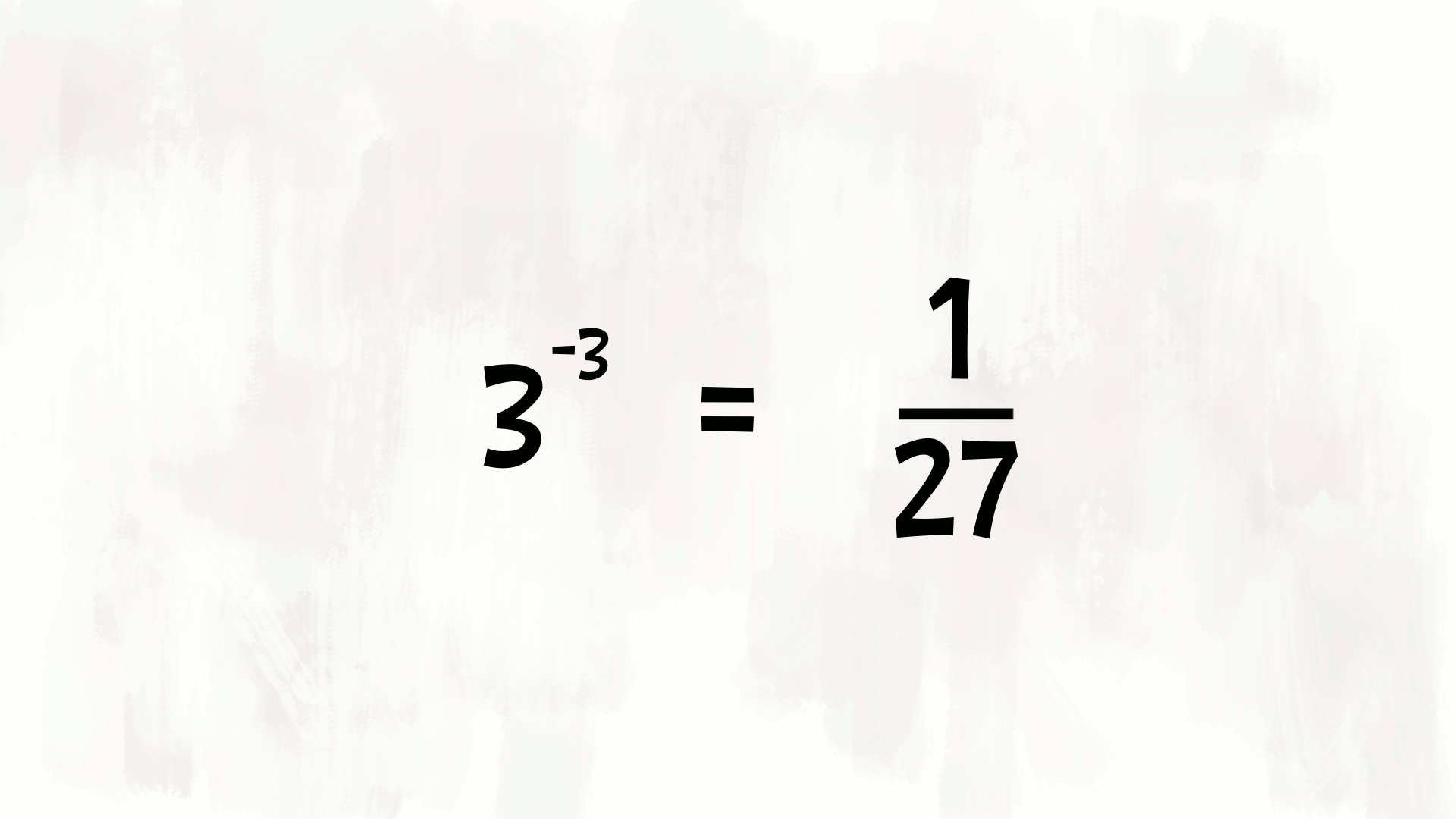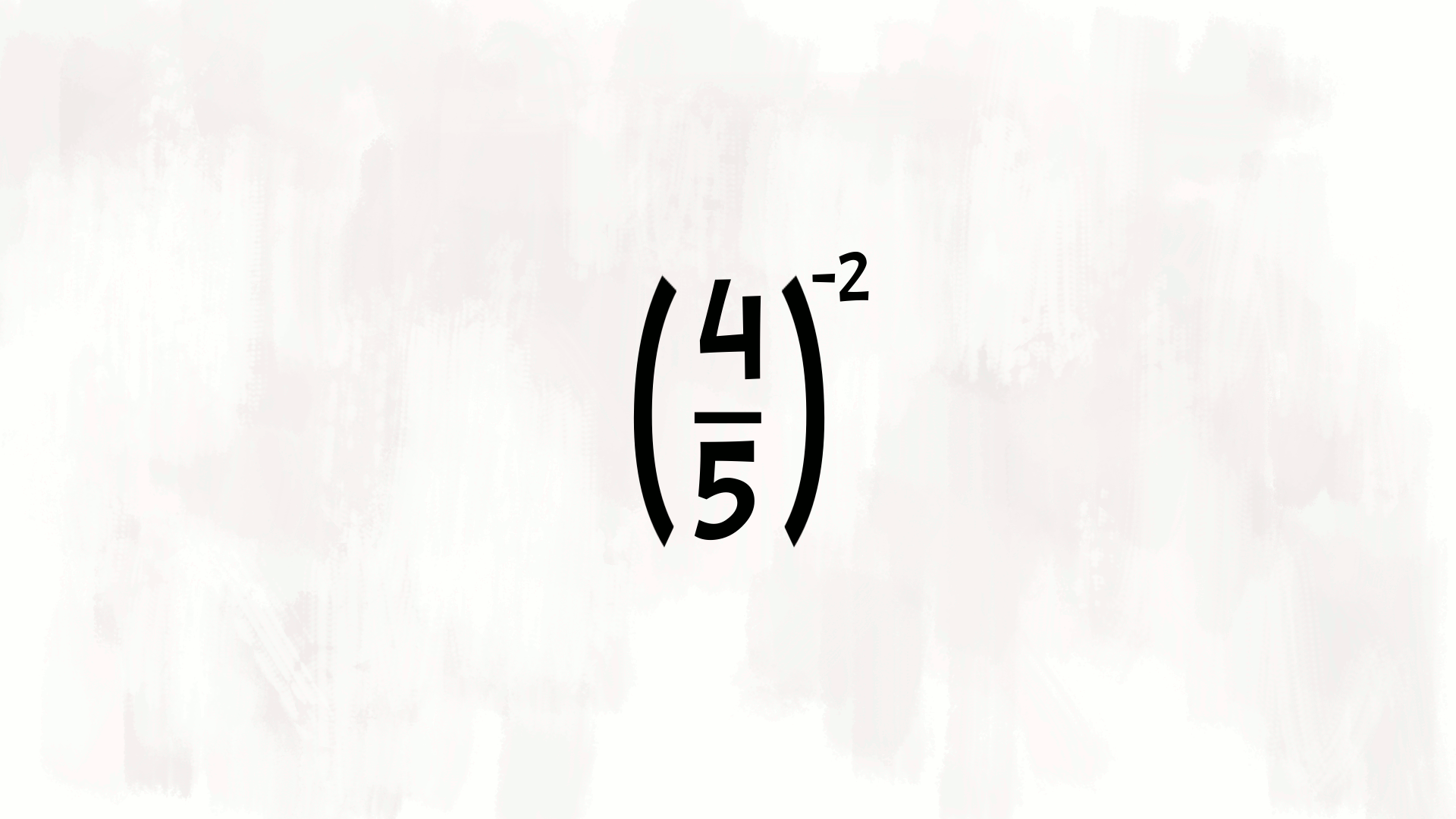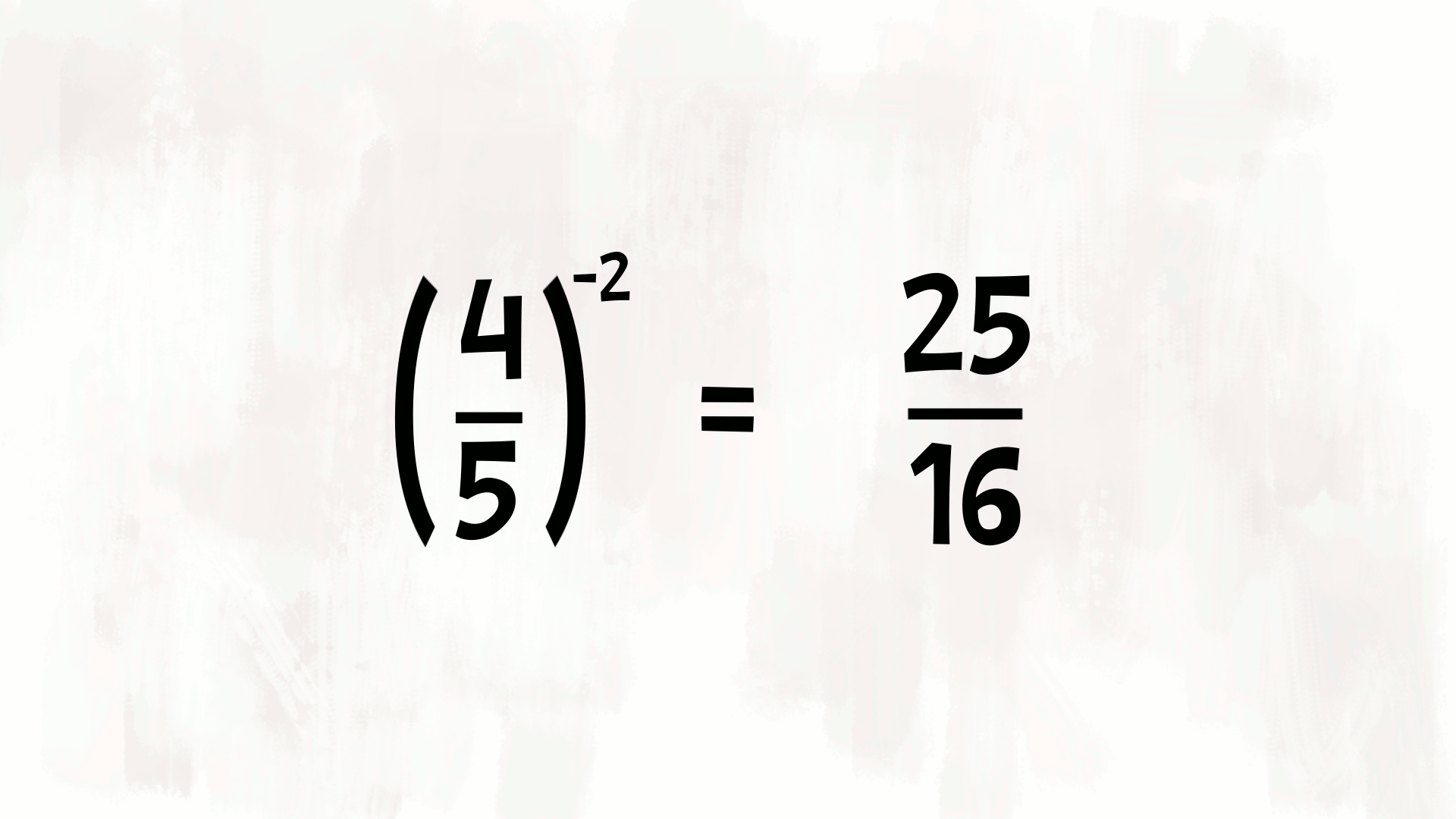
E se l’esponente di una potenza fosse un numero intero negativo?
Che cosa vuol dire la scrittura £$ (+5)^{-2} $£?
La potenza con esponente intero negativo e con base intera è una frazione!
$$ (+5)^{-2} =+\frac{1}{5^2}=+\frac{1}{25}$$
Al numeratore scriviamo il numero £$ 1 $£ e al denominatore scriviamo la stessa potenza ma con esponente positivo.
Esempio: £$ (-3)^{-4} =+\frac{1}{(-3)^4}=+\frac{1}{81}$£
E che cosa succede se la potenza con esponente intero negativo ha come base una frazione?
Dobbiamo considerare la frazione reciproca, quella che si ottiene scambiando il numeratore con il denominatore.
$$ \left(-\frac{2}{5}\right)^{-3} = \left(-\frac{5}{2}\right)^3 = -\frac{125}{8} $$
Quindi, la potenza negativa di un numero è uguale alla potenza positiva del reciproco della base!
Proprietà delle potenze di numeri relativi
Inoltre valgono tutte le proprietà delle potenze che hai visto fino ad ora!
Prodotto di potenze con la stessa base
£$ (-2)^{+2} \cdot (-2)^{-3} = (-2)^{(+2) + (-3)} = (-2)^{-1} $£
Divisione di potenze con la stessa base
£$ (-2)^{+2} : (-2)^{-3} = (-2)^{(+2) – (-3)} = (-2)^{+5} $£
Prodotto di potenze con stesso esponente
£$ (-2)^{-3} \cdot (+3)^{-3} = ((-2) \cdot (+3))^{-3} = (-6)^{-3} $£
Divisione di potenze con stesso esponente
£$ (-2)^{-3} : (+3)^{-3} = ((-2) : (+3))^{-3} = \left(-\frac{2}{3}\right)^{-3} $£
Potenza di potenza
£$ \left[(-2)^{-3}\right]^{+2} = (-2)^{(-3) \cdot (+2)}=(-2)^{-6} $£
Interrogazione sulle potenze di numeri relativi interi
Sei pronto ad affrontare l’interrogazione? Invece di dire “mi giustifico", leggi le possibili domande che ti possono fare e prova a rispondere. Se hai dubbi, riguarda le lezioni oppure allenati con gli esercizi!
Numeri relativi: vai con la sfida!
Sfida:
Soluzione:
Il tuo amico Fabio ti presta delle camicie. Ogni volta ne prendi sempre il doppio rispetto alla volta precedente. Quante camicie avrai la quarta volta?
Prova a risolvere la sfida sui numeri relativi e le operazioni. Allenati guardando i video e facendo gli esercizi e poi controlla se hai trovato la soluzione esatta!
