Moltiplicazioni e divisioni con i numeri relativi
La moltiplicazione e la divisione con i numeri relativi sono concetti fondamentali dell’aritmetica che giocano un ruolo cruciale nella comprensione delle operazioni matematiche più avanzate. I numeri relativi includono l’insieme dei numeri interi, che si estendono oltre i numeri naturali per includere gli interi negativi e lo zero. Questi numeri sono essenziali per descrivere situazioni che vanno oltre il conteggio e le misurazioni positive, come i debiti o le temperature sotto lo zero.
Quando si moltiplicano o dividono numeri relativi, è importante considerare non solo la grandezza dei numeri, ma anche i loro segni. La regola fondamentale da ricordare è che il prodotto o il quoziente di due numeri con lo stesso segno è sempre positivo, mentre il prodotto o il quoziente di due numeri con segni opposti è negativo. Questo significa che moltiplicare o dividere due numeri positivi o due numeri negativi produce un risultato positivo, mentre moltiplicare o dividere un numero positivo per un numero negativo (o viceversa) dà come risultato un numero negativo.
La moltiplicazione di numeri relativi si basa sull’addizione ripetuta: moltiplicare un numero per un altro significa sommare quel numero a se stesso tante volte quante indicate dal secondo numero. Per esempio, £$3×4$£ equivale a sommare 3 a se stesso volte, risultando in 12. Quando si moltiplicano numeri negativi, si applica la stessa logica, tenendo presente la regola dei segni; così, £$−3×−4$£ diventa l’addizione ripetuta di −3 per volte, che dà 12 perché stiamo moltiplicando due numeri negativi.
Per quanto riguarda la divisione, il concetto è quello di determinare quante volte un numero (il divisore) è contenuto in un altro numero (il dividendo). La divisione di numeri relativi segue la stessa regola dei segni della moltiplicazione. Dividere 12 per 3 ci dice quante volte è contenuto in 12, che è . Analogamente, dividere −12 per − segue la stessa logica, con il risultato positivo di , poiché entrambi i numeri sono negativi.
Ma non preoccuparti, vediamo passo per passo come fare!
Come calcolare il prodotto di numeri relativi
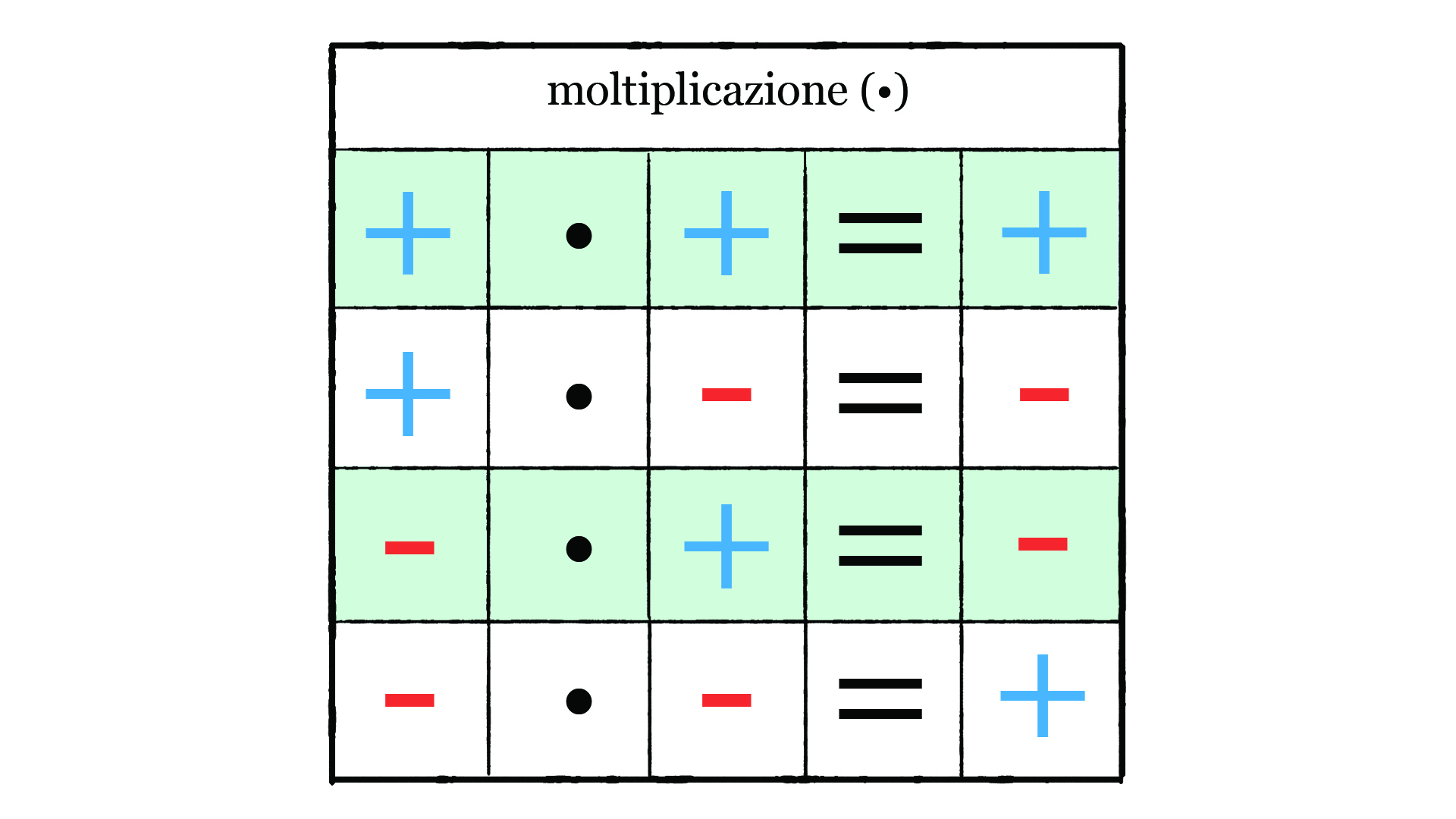
Fare le moltiplicazioni con i numeri interi può essere molto divertente!
Ti basta ricordare come fare le moltiplicazioni tra numeri naturali e poi imparare una semplice regolina: la regola dei segni.
Se i segni dei fattori sono concordi, il risultato è positivo.
Se i segni dei fattori sono discordi, il risultato è negativo.
Per fare una moltiplicazione con i numeri interi:
- decidiamo il segno del risultato con la regola dei segni;
- calcoliamo il prodotto tra i valori assoluti dei fattori.
Esempi:
£$ (+5) \cdot (+2) = +10 $£
£$ (-5) \cdot (-2) = +10 $£
£$ (+5) \cdot (-2) = -10 $£
£$ (-5) \cdot (+2) = -10 $£
Ricorda! Alcune delle regole che abbiamo già imparato, valgono anche per le moltiplicazioni tra numeri interi.
Qualsiasi numero moltiplicato per £$ 0 $£ dà come risultato £$ 0 $£.
£$ (+5)\cdot 0 = 0$£
£$ (-5)\cdot 0 = 0$£
Abbiamo imparato che £$ 1$£ è l’elemento neutro della moltiplicazione.
Questa proprietà vale anche per i numeri relativi: la moltiplicazione per £$ 1 $£ dà come risultato il numero stesso!
£$ (+5)\cdot (+1) = +5 $£
£$ (-5)\cdot (+1) = -5 $£
È un discorso diverso per la moltiplicazione per £$ -1 $£.
La moltiplicazione per questo numero dà come risultato il numero di partenza, ma con il segno opposto!
£$ (+5)\cdot (-1) = -5 $£
£$ (-5)\cdot (-1) = +5 $£
Moltiplicare per £$ -1 $£ equivale a cambiare il segno!
Le proprietà della moltiplicazione
La moltiplicazione tra numeri interi e razionali, positivi e negativi, ha le stesse proprietà che abbiamo già imparato in prima media.
Proprietà commutativa
£$ (-5)\cdot(+2)=(+2)\cdot(-5) = -10 $£
Proprietà associativa
£$ [(-5)\cdot(+2)]\cdot (-3)=(-5)\cdot[(+2)\cdot(-3)] = +30 $£
Proprietà distributiva rispetto all’addizione
£$ (-5)\cdot[(+2)+(-3)] =[(-5)\cdot(+2)]+ [(-5)\cdot(-3)]= +5 $£
Come calcolare il quoziente di numeri relativi
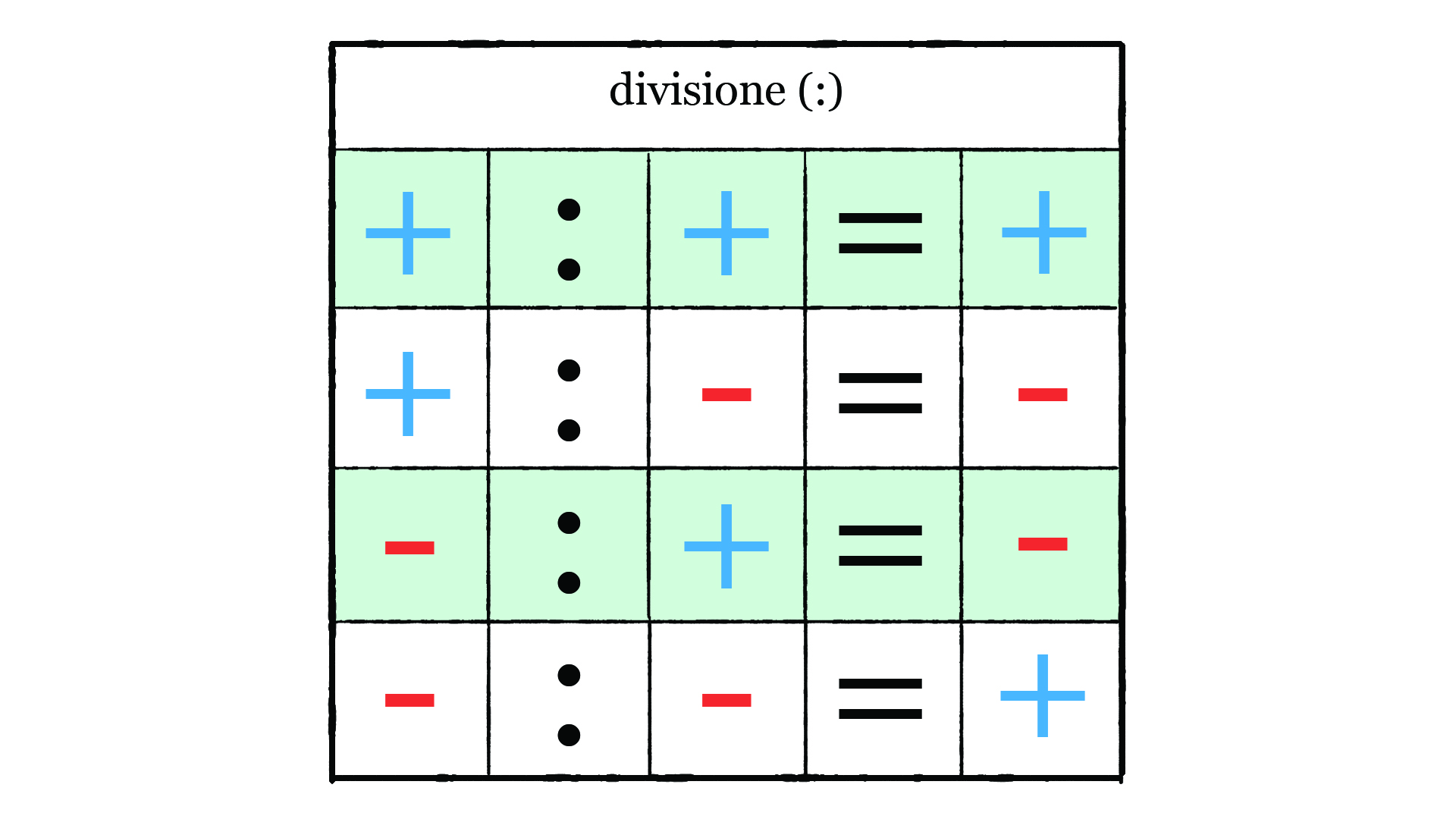
Forse ora stai già immaginando come si fanno le divisioni con i numeri interi…
Anche questa volta ti basta ricordare come fare le divisioni tra numeri naturali e conoscere la regola dei segni per la divisione.
Per fare una divisione con i numeri interi:
- decidiamo il segno del risultato con la regola dei segni;
- calcoliamo la divisione tra i valori assoluti dei fattori.
Esempi:
£$ (+10) : (+2) = +5 $£
£$ (-10) : (-2) = +5 $£
£$ (+10) : (-2) = -5 $£
£$ (-10) : (+2) = -5 $£
Ricorda! Alcune delle regole che abbiamo già imparato, valgono anche per le divisioni tra numeri interi.
Il quoziente tra due numeri interi non è sempre un numero intero. Prima di tutto, non si può mai dividere per £$ 0 $£!
£$ (+10) : 0 $£ non ha significato.
Inoltre, ad esempio, il quoziente £$ (+5) : (-3) $£ non è un numero intero!
Come hai già visto quando hai studiato la divisione, il numero £$ 0 $£ diviso per qualsiasi altro numero diverso da £$, dà [iol_placeholder type="formula" engine="katex" display="inline"] 0 $£ come risultato!
£$ 0 : (+5) = 0$£
£$ 0 : (-5) = 0$£
Qualsiasi numero diviso per £$ +1 $£ dà come risultato il numero stesso!
£$ (+5) : (+1) = +5 $£
£$ (-5) : (+1) = -5 $£
E la divisione per £$-1$£? Come per la moltiplicazione, qualsiasi numero diviso per £$ -1 $£ dà come risultato il suo opposto!
£$ (+5) : (-1) = -5 $£
£$ (-5) : (-1) = +5 $£
Anche dividere per £$ -1 $£ equivale a cambiare il segno!
Moltiplicazioni e divisioni con i numeri razionali e relativi
Moltiplicare e dividere numeri razionali positivi o negativi è un gioco da ragazzi!
Basta ricordare le moltiplicazioni e le divisioni tra frazioni, le regole dei segni e che £$ -\dfrac{a}{b} = \dfrac{-a}{b} = \dfrac{a}{-b} $£.
Per moltiplicare due frazioni ricorda che puoi semplificare in croce per velocizzare i calcoli.
Possiamo trasformare la divisione tra due frazioni nella moltiplicazione della prima frazione per il reciproco della seconda.
Esempi:
£$-\dfrac{2}{3} \cdot \dfrac{6}{5}=-\dfrac{2\cdot 6}{3\cdot5}=-\dfrac{12}{15}=-\dfrac{4}{5}$£
£$-\dfrac{2}{3} : \left(-\dfrac{8}{9}\right) =-\dfrac{2}{3} \cdot \left(-\dfrac{9}{8}\right) = $£ £$ +\dfrac{2\cdot 9}{3\cdot8}=+\dfrac{18}{24}=+\dfrac{3}{4}$£
