Le frazioni: cosa sono, come si usano e a cosa servono
Una frazione è una divisione tra due numeri interi. Quali sono i tipi di frazioni che conosci? Impara a scrivere le frazioni distinguendo il numeratore ed il denominatore. Non dimenticare di scrivere la linea, o riga, di frazione!
Una frazione rappresenta una parte di un intero o, più generalmente, qualsiasi numero di parti uguali. Consiste di un numeratore e un denominatore, separati da una linea di frazione. Il numeratore indica quante parti sono prese, mentre il denominatore indica in quante parti uguali è diviso l’intero.
Ad esempio, la frazione £$\frac34$£ significa che si prendono 3 parti di un intero diviso in 4 parti uguali. Le frazioni sono utilizzate in svariati contesti, dalla vita quotidiana all’ingegneria, e comprendere le basi delle frazioni è essenziale per lo sviluppo delle competenze matematiche anche più complesse ed avanzate: tutti i più grandi matematici sono passati prima, come tutti, dallo studio delle frazioni!
Consulta, scarica e stampa la mappa mentale delle frazioni. Tienila sempre sotto mano per non dimenticare niente.
- Cosa sono le frazioni e quali sono le loro caratteristiche
- La ricetta della pizza con le frazioni: cosa sono
- Frazioni proprie, improprie e apparenti
- Frazioni proprie
- Frazioni apparenti
- Frazioni improprie
- Come calcolare la frazione di un numero?
- Frazioni con lo 0 al numeratore o al denominatore
- Come semplificare una frazione
- L'uso delle frazioni nella musica
- Dalla frazione all’intero
- Mappa per ripassare le frazioni
- Scheda attività - impara ad utilizzare le frazioni
Cosa sono le frazioni e quali sono le loro caratteristiche
Cosa sono le frazioni? Il termine frazione deriva dal latino fractio, participio passato di frangere, che significa “spezzare". Le frazioni, infatti rappresentano le parti in cui spezziamo un intero.
Una frazione è un modo diverso per scrivere una divisione. Se devi dividere £$9 $£ pizze tra £$3$£ persone sai che ognuna avrà £$3$£ pizze, perché £$9:3=3$£.
Ma se devi dividere £$3$£ pizze tra £$9$£ persone? Devi dividere ogni pizza in £$3$£ spicchi, così avrai £$9$£ spicchi in tutto e ogni persona potrà riceverne £$1$£.
Come si chiamano questi spicchi? Sono parti dell’intero e per indicarle, in matematica, utilizziamo le frazioni! Ognuno avrà un terzo di pizza!
La frazione è composta dal numeratore e dal denominatore, il denominatore ti dice qualcosa sull’intero, mentre il numeratore descrive le parti che stai prendendo. Confronta il numeratore ed il denominatore e scopri la differenza tra frazione propria, frazione apparente e frazione impropria.
Fai sempre attenzione allo 0: non esistono frazioni con denominatore uguale a 0 perché la divisione per 0 è impossibile!
La ricetta della pizza con le frazioni: cosa sono
Una frazione è un modo per esprimere una quantità dividendo un intero in un certo numero di parti uguali. Scriviamo una frazione in questo modo: £$ \frac{2}{5} $£, la linea fra i due numeri viene chiamata riga, o linea di frazione.
Il numero che si trova sotto alla riga di frazione si chiama denominatore e indica in quante parti uguali è stato suddiviso l’intero. Infatti il termine denominatore deriva da denominare, quindi dare un nome alle parti in cui abbiamo diviso l’intero (terzi, quarti, quinti…). Il numero che si trova sopra, invece, si chiama numeratore (che deriva da enumerare, cioè contare) e indica quante di queste parti consideriamo nella nostra frazione.
Le frazioni non sono altro che divisioni indicate con la linea di frazione anziché con il £$:$£. Per esempio, £$4:2=\frac{4}{2}=2$£; £$1:2=\frac{1}{2}=0,5$£; £$5:5=\frac{5}{5}=1$£. Le frazioni sono molto comode quando hai una divisione che ha come risultato un numero con la virgola!
Frazioni proprie, improprie e apparenti
Le frazioni possono essere:
- frazioni proprie: il numeratore è minore del denominatore. Esempio: £$ \frac{4}{7} $£
- frazioni apparenti : il numeratore è uguale o un multiplo del denominatore. Esempio: £$ \frac{9}{3} = 3 $£ Possiamo scrivere tutti i numeri interi sotto forma di frazione!
- frazioni improprie: il numeratore è maggiore del denominatore. Esempio: £$ \frac{12}{5} $£
Abbiamo detto che le frazioni sono delle divisioni. Le divisioni possono avere come risultato un numero intero, oppure un numero con la virgola. Per esempio: £$3:3=1$£; £$4:2=2$£; £$2:4=0,5 $£ e £$5:2= 2,5$£. Cosa noti? Le divisioni possono avere un risultato più grande o più piccolo di £$1$£ a seconda che il divisore sia maggiore o minore del dividendo. È la stessa cosa che accade nelle frazioni:
-
- le frazioni proprie sono quelle che rappresentano un numero più piccolo di £$1$£, perché prendiamo solo alcune parti dell’intero;
- le frazioni improprie rappresentano un numero più grande di £$1$£, infatti ho bisogno di più di un intero per rappresentarle;
- le frazioni apparenti sono quelle che rappresentano un numero intero!
Ma vediamo un po’ più nel dettaglio queste tre tipologie diverse di frazione.
Frazioni proprie
In una frazione riconosciamo numeratore e denominatore. Quando il numeratore è minore del denominatore siamo di fronte ad una frazione propria.
Esempio: £$ \dfrac{4}{7} $£, il numeratore è minore del denominatore perché [iol_placeholder type="formula" engine="katex" display="inline"] 4
Abbiamo detto che utilizziamo le frazioni per indicare una parte dell’intero: suddividiamo un intero in un certo numero di parti uguali (indicate dal denominatore), poi ne scegliamo un certo altro numero (indicato dal numeratore). Diciamo che la frazione è propria perché indica una parte che è minore dell’intero: ci basta un solo intero per rappresentare questo genere di frazioni.
Le frazioni proprie sono quelle che rappresentano un numero più piccolo di £$1$£, perché prendiamo solo alcune parti dell’intero.
Esempio: [iol_placeholder type="formula" engine="katex" display="inline"] \dfrac{4}{16} = 0,25
Frazioni apparenti
Come dice il nome stesso, una frazione apparente è una frazione solo in apparenza, perché rappresenta un numero intero. Il numeratore è uguale o multiplo del denominatore.
Esempio: £$ \dfrac{9}{3} = 3 $£
Possiamo scrivere tutti i numeri interi sotto forma di frazione! Le frazioni apparenti sono quelle che rappresentano un numero intero, maggiore o uguale a £$ 1 $£.
Frazioni improprie
Siamo arrivati al termine della classificazione delle frazioni. Le frazioni improprie sono quelle frazioni in cui il numeratore è maggiore del denominatore.
Esempio: £$ \dfrac{12}{5} $£ è una frazione impropria perché £$ 12 > 5 $£.
Diciamo che sono frazioni improprie perché occorre più di un intero per rappresentarle. Le frazioni improprie, infatti, indicano un numero maggiore di £$ 1 $£.
Esempio: £$ \dfrac{12}{5} = 2,4 > 1 $£
Come calcolare la frazione di un numero?

Oscar ha 12 gabbie di mosche. I £$ \dfrac 34 $£ di queste sono vuote. Quante gabbie sono piene?
Per risolvere questo problema, dobbiamo rispondere alla domanda: quanto è £$ \dfrac 34 $£ di 12? Il nostro intero è formato dalle 12 gabbiette. Dobbiamo calcolarne i £$ \dfrac 34 $£.
Prima di tutto individuiamo quante gabbiette compongono l’unità frazionaria, cioè £$ \dfrac 14 $£. Come? Basta dividere il nostro intero in 4 parti uguali, cioè risolvere la divisione 12 : 4 = 3. L’unità frazionaria è costituita da 3 gabbiette, quindi l’intero è suddiviso in 4 parti uguali, ciascuna con 3 gabbiette.
Per calcolare i £$ \dfrac 34 $£, moltiplichiamo la nostra unità frazionaria per 3, cioè 3 x 3 = 9.
I £$ \dfrac 34 $£ di 12 sono 9 gabbiette. Significa quindi che 9 gabbiette sono vuote, di conseguenza 12 – 9 = 3, rimangono 3 gabbiette piene.
In verità per risolvere questo problema era sufficiente individuare l’unità frazionaria: infatti se £$ \dfrac 34 $£ delle gabbiette sono vuote, significa che le altre sono piene, e sono indicate dalla frazione complementare che è proprio £$ \dfrac 14 $£.
Per calcolare la frazione di un numero, dividiamo quel numero per il denominatore e poi lo moltiplichiamo per il numeratore della frazione.
Frazioni con lo 0 al numeratore o al denominatore
Il numeratore di una frazione può essere nullo? Esiste una frazione con denominatore uguale a [iol_placeholder type="formula" engine="katex" display="inline"/]?
Nelle frazioni può comparire anche lo 0, ma bisogna fare molta attenzione!
Le frazioni con lo 0 al numeratore sono sempre uguali a 0. Scrivere £$ \frac{0}{8} $£ è come scrivere £$ 0 $£: prendo £$ 0 $£ parti di un intero.
Qual è una delle prime regole che hai imparato studiando le divisioni? Non si può dividere per 0! Quindi non esistono frazioni con lo 0 al denominatore: £$ \frac{4}{0} $£ è impossibile!
Come semplificare una frazione
Una frazione è una divisione e quindi puoi applicare la proprietà invariantiva: dividendo numeratore e denominatore per uno stesso numero il risultato non cambia, cioè si ottiene una frazione equivalente a quella di partenza. Questo processo si chiama semplificazione di una frazione. Per esempio, data la frazione £$\frac{21}{42}$£, puoi semplificarla dividendo numeratore e denominatore per £$7$£, quindi otterrai £$\frac{3}{6}$£.
Dividendo entrambi i termini della frazione per il loro M.C.D. (Massimo Comune Divisore), non potrai semplificare ulteriormente la frazione che si dice ridotta ai minimi termini.
In una frazione ridotta ai minimi termini il M.C.D. tra numeratore e denominatore è £$1$£, cioè non ci sono altri divisori comuni e quindi non può essere ulteriormente semplificata. La frazione £$\frac{3}{6}$£ non è ridotta i minimi termini, infatti £$ \text{M.C.D.}(3, 6) = 3 \ne 1$£.
Riprendiamo l’esempio di partenza. Semplifichiamo la frazione £$\frac{21}{42}$£ finché non è ridotta ai minimi termini. Il £$ \text{M.C.D.}(21, 42) =7 \cdot 3=21$£ allora dividendo numeratore e denominatore per £$21$£ si ottiene la frazione equivalente £$\frac{1}{2}$£, che è ridotta ai minimi termini.
L’uso delle frazioni nella musica
Valori delle note e delle pause
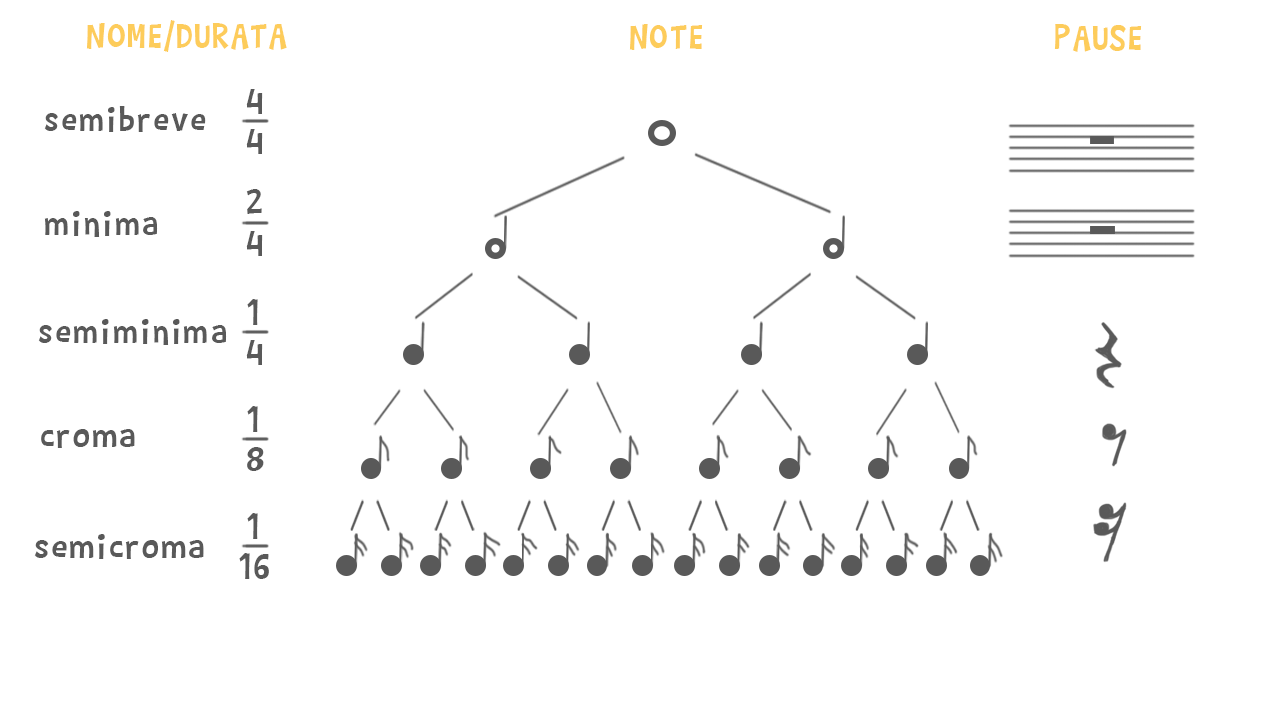
Esempi di spartito

Le frazioni sono utili anche per leggere la musica. Conosci il pentagramma? È lo spazio in cui scriviamo la musica: è formato da £$ 5 $£ linee parallele e £$ 4 $£ spazi. È suddiviso con stanghette verticali che indicano le battute. All’inizio del pentagramma troviamo la chiave di violino (o chiave di sol) che serve a fissare la posizione delle note (esistono anche la chiave di basso o chiave di fa e le chiavi di do) e una frazione che indica la durata di ciascuna battuta. Le durate più comuni sono £$ \frac{4}{4} , \frac{3}{4}, \frac{2}{4} $£, ma anche £$ \frac{3}{8}, \frac{6}{8} $£… In ogni battuta, quindi, può starci un certo numero di note: anche queste hanno un valore e un nome diverso in base alla durata! Per esempio, in una battuta da £$ \frac{4}{4} $£ possiamo scrivere £$ 4 $£ note da £$ \frac{1}{4} $£, oppure £$ 2 $£ note da £$ \frac{2}{4} $£. In musica non ci sono solo le note: anche le pause hanno valori diversi e scritture diverse. Per completare una battuta possiamo inserire note e pause di valori diversi.
Il puntino scritto dopo una nota allunga il suo valore della metà della nota stessa. Per esempio una minima £$ \left( \frac{2}{4} \right) $£ seguita da un puntino vale £$ \frac{2}{4} + \frac{2}{4} : 2 $£. La metà di £$ \frac{2}{4} $£ è £$ \frac{1}{4} $£, quindi una minima con un puntino vale £$ \frac{3}{4} $£.
Guarda lo schema delle durate delle note e prendi confidenza con le frazioni che indicano i tempi musicali. Prova a leggere i due spartiti e non perdere neanche una frazione di secondo! Impara come leggere la musica iniziando a capire a cosa servono le frazioni all’inizio del pezzo!
Frazioni con lo stesso numeratore a confronto
Puoi confrontare due frazioni anche senza fare la divisione fra numeratore e denominatore. Basta analizzare i loro numeratori e denominatori e scegliere la giusta scorciatoia!
Se due frazioni hanno lo stesso numeratore, la frazione che ha il denominatore maggiore è quella più piccola. Infatti, più grande è il denominatore, più sono le parti in cui abbiamo suddiviso l’intero, quindi tutte le parti sono più piccole. Nel confronto tra frazioni con lo stesso numeratore “vince" quella con il denominatore più piccolo.
Esempio: Ci sono due torte, una divisa in £$ 7 $£ fette e l’altra divisa in £$ 9 $£ fette. Puoi prendere al massimo £$ 2 $£ fette. Da quale torta ti conviene prenderle? Le fette della torta divisa in £$ 7 $£ parti saranno sicuramente più grosse di quelle della torta divisa in £$ 9 $£ parti: £$ \frac{2}{7} > \frac{2}{9} $£
Dalla frazione all’intero

Oscar ha avanzato 32 caramelle, cioè i £$ \dfrac 25 $£ del pacchetto. Quante caramelle c’erano in tutto inizialmente nel pacchetto?
Conosciamo il valore della frazione di un numero, vogliamo risalire al numero da cui siamo partiti, cioè all’intero. Come possiamo fare? Dobbiamo seguire il procedimento inverso di prima! Visto che il denominatore della frazione è uguale a 5, sappiamo che l’intero è suddiviso in 5 parti uguali, ma di queste ne abbiamo considerate 2: possiamo quindi trovare quanto vale l’unità frazionaria con una divisione 32 : 2 = 16. L’intero è formato quindi da 5 parti uguali a 16, quindi il nostro intero è 16 x 5 = 80.
Inizialmente nel sacchetto di caramelle c’erano in tutto 80 caramelle.
Per risalire all’intero da una sua frazione, dividiamo il numero che abbiamo per il numeratore e poi moltiplichiamo il risultato per il denominatore della frazione.
Mappa per ripassare le frazioni
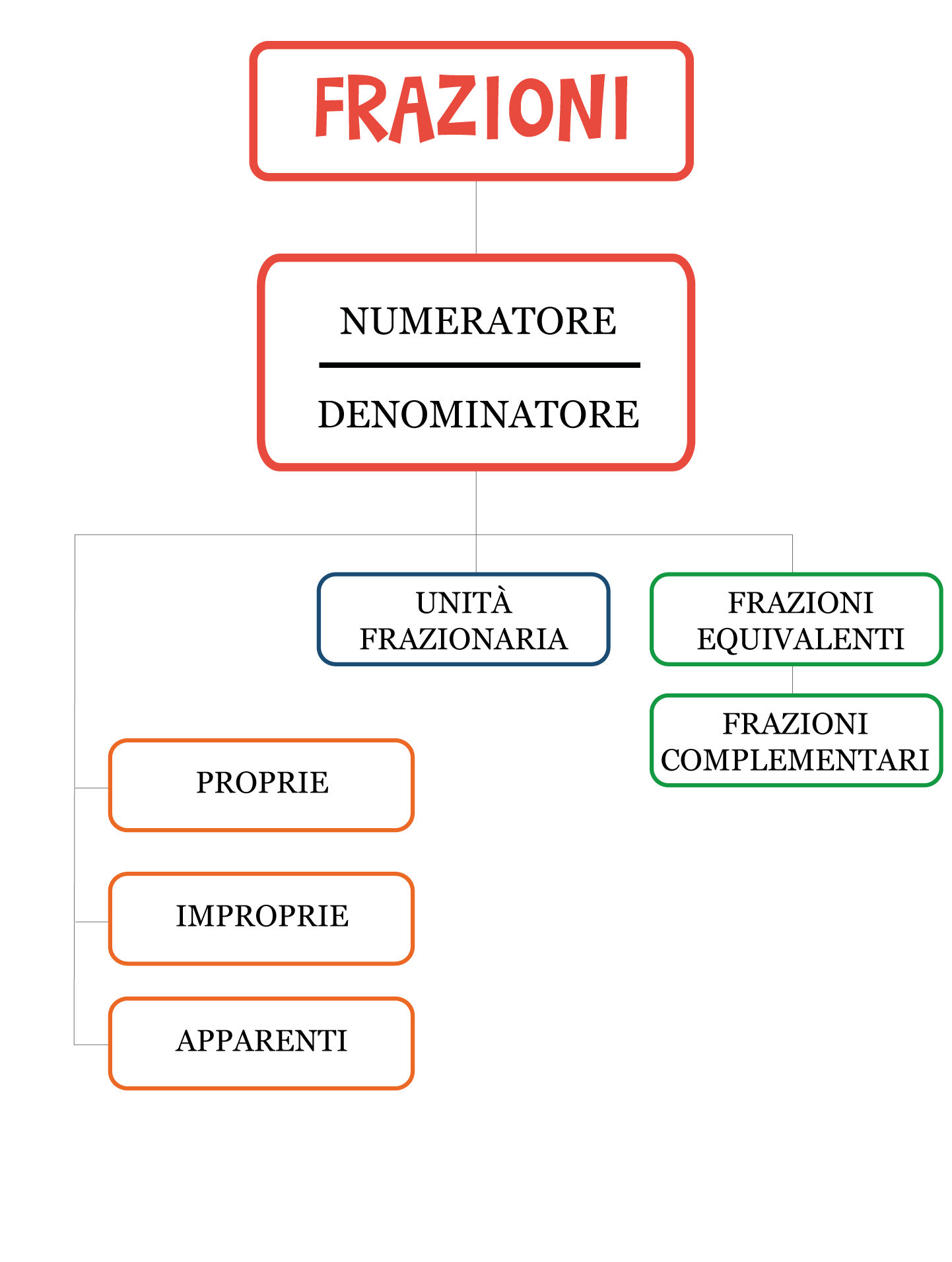
Qui puoi scaricare la mappa per ripassare le frazioni:
Scheda attività – impara ad utilizzare le frazioni
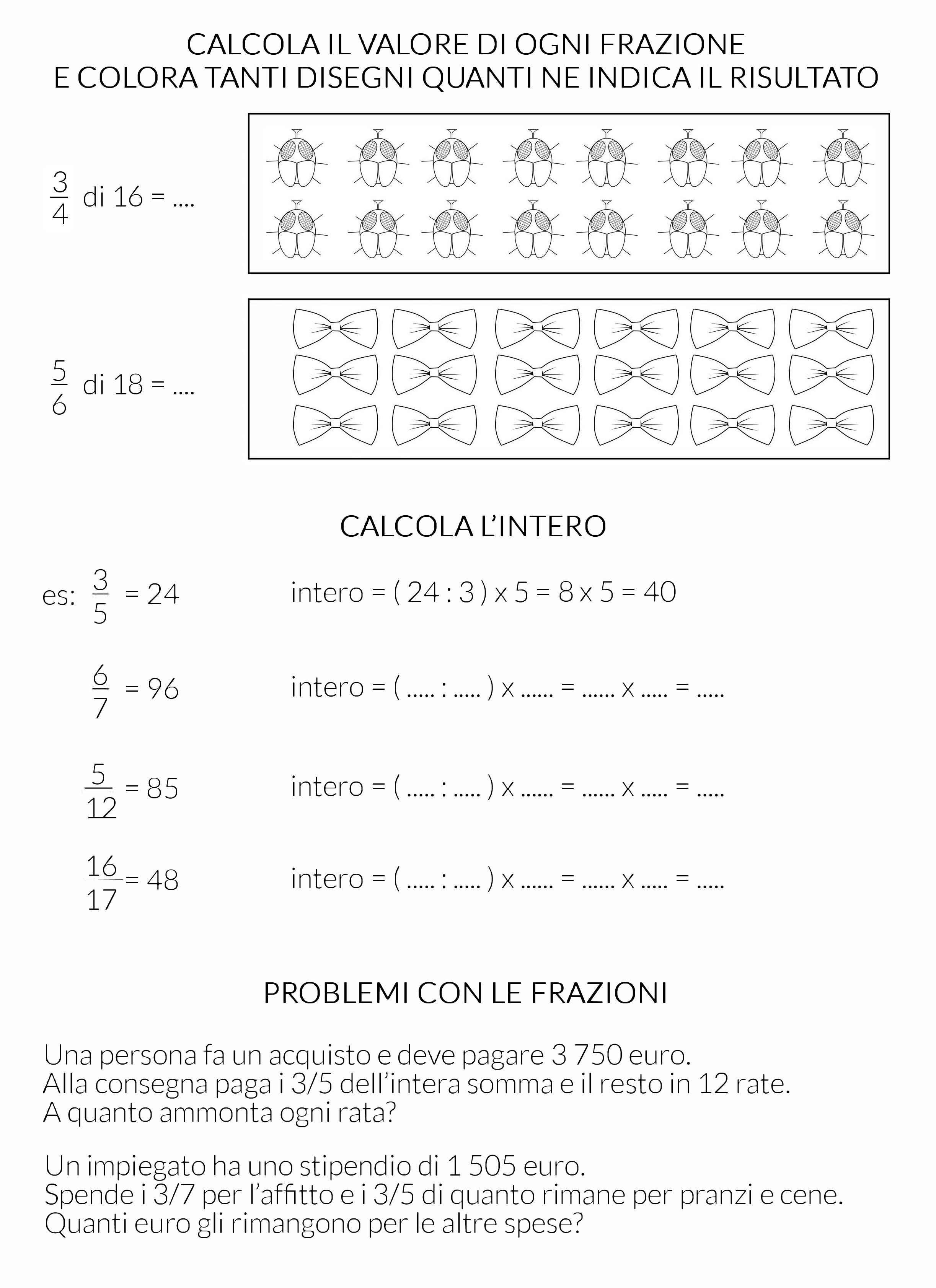
Nella scheda qualche esercizio per imparare a calcolare dapprima la frazione di un numero come applicazione del procedimento, poi all’interno di un problema più complesso.
Scaricala qui:
Feste di compleanno e frazioni: la sfida
Sfida:
Soluzione:
È il tuo compleanno e devi comprare il necessario per preparare i cocktail. Tutte le ricette usano un quarto di questo, la metà di quello, ci sono frazioni ovunque! Leggi la sfida e poi guarda i video sulle frazioni. Impara cosa è una frazione, quali sono le proprietà delle frazioni, cosa significa semplificare e quali sono le frazioni ridotte ai minimi termini. Tutte queste cose ti aiuteranno a risolvere l’esercizio della sfida matematica di cui trovi anche la soluzione!
