I poligoni: cosa sono e come calcolarne il perimetro
Un poligono, per definizione, è una figura geometrica piana chiusa, costituita da una sequenza finita di segmenti di linea che si intersecano solo alle loro estremità. Ogni segmento è chiamato lato del poligono, mentre i punti di intersezione sono i suoi vertici. Non c’è limite al numero di lati che un poligono può avere: in teoria, potrebbero essere da tre (come in un triangolo, il più semplice dei poligoni) a molti di più, fino ad arrivare anche a dodici (come nel caso del dodecagono)!
Ciò che rende affascinante l’universo dei poligoni è la loro diversità. Sono presenti in una vasta gamma di forme e formati, con caratteristiche che li rendono unici. Ad esempio, esistono poligoni regolari, in cui tutti i lati e gli angoli sono uguali, e poligoni irregolari, in cui i lati e gli angoli possono variare. Allo stesso modo, alcuni poligoni sono convessi (non hanno angoli interni superiori a 180 gradi) mentre altri sono concavi (hanno almeno un angolo interno superiore a 180 gradi).
Il calcolo del perimetro di un poligono è un altro concetto importante che affronteremo in questo articolo. Il perimetro, semplicemente, è la somma delle lunghezze di tutti i lati del poligono. Ogni tipo di poligono ha una formula specifica per calcolare il suo perimetro, ma una volta imparato qualche trucchetto vedrai che sarà molto più semplice di quanto pensi!
Vuoi testare la tua preparazione? Prova a rispondere alle domande del nostro quiz!
- Che cos'è un poligono?
- Poligoni convessi e poligoni concavi
- Poligoni equilateri, equiangoli, regolari
- Perimetro di un poligono
Che cos’è un poligono?
Dopo aver imparato a distinguere punti, segmenti e angoli, possiamo combinare questi elementi e troviamo i poligoni. Cosa sono?
Iniziamo dalla parola poligono: deriva dal greco polygonos che significa “molti angoli". Infatti un poligono è la parte di piano delimitata da una linea spezzata chiusa non intrecciata. Queste linee spezzate (aperte o chiuse) non intrecciate, infatti, si chiamano anche poligonali. In una poligonale riconosciamo molti lati e molti angoli! 😉
Scopriamo tutti gli elementi di un poligono:
- ogni segmento della linea spezzata si chiama lato;
- gli estremi comuni di ciascuna coppia di lati si chiamano vertici (e si indicano con le lettere maiuscole perché sono dei punti);
- gli angoli delimitati da due lati consecutivi sono gli angoli interni;
- gli angoli delimitati da un lato e dal prolungamento del suo consecutivo, invece, sono gli angoli esterni;
- i segmenti che congiungono due vertici non consecutivi si chiamano diagonali.
Come facciamo a capire di che tipo di poligono stiamo parlando? Possiamo classificare i poligoni in base al numero di lati:
- un triangolo è un poligono con 3 lati e 3 angoli;
- un quadrilatero è un poligono con 4 lati e 4 angoli;
- un pentagono è un poligono con 5 lati e 5 angoli;
- un esagono è un poligono con 6 lati e 6 angoli;
- un ettagono è un poligono con 7 lati e 7 angoli;
- un ottagono è un poligono con 8 lati e 8 angoli;
- un ennagono è un poligono con 9 lati e 9 angoli;
- un decagono è un poligono con 10 lati e 10 angoli.
Un poligono è formato da un certo numero di lati, cioè di segmenti consecutivi, che formano una linea spezzata chiusa. Ma è sempre possibile costruire un poligono? Per riuscire a disegnare una linea spezzata chiusa, è necessario che ciascun lato sia minore della somma di tutti gli altri lati del poligono. Prova a disegnare un quadrilatero con i lati di £$ 2 \text{ cm}, 6 \text{ cm}, 10 \text{ cm} $£ e £$ 20 \text{ cm} $£. Impossibile, vero? Perché £$ 20 \text{ cm} > (6 + 2+ 10) \text{ cm} $£.
Poligoni convessi e poligoni concavi
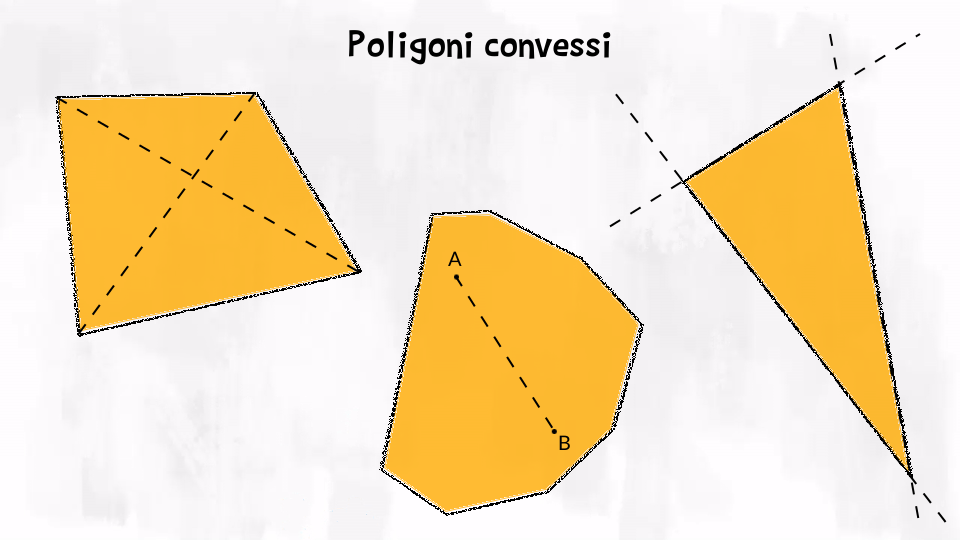
Poligoni convessi
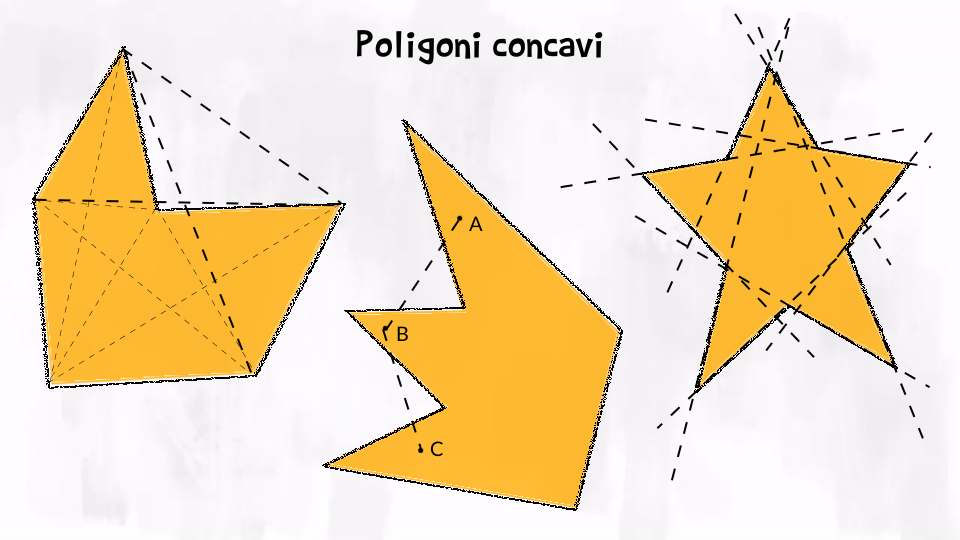
Poligoni concavi
Come riconoscerli?
Abbiamo parlato di angoli convessi e angoli concavi. I poligoni sono figure con molti angoli, quindi possono essere convessi o concavi. Come facciamo a riconoscerli? Funziona esattamente come per gli angoli!
Un poligono è convesso se tutti i suoi angoli interni sono convessi, cioè se i prolungamenti due suoi lati restano esterni al poligono. Riconosciamo velocemente un poligono convesso disegnando le sue diagonali: sono tutte all’interno del poligono. C’è anche un altro modo: controlliamo se il segmento che congiunge una qualsiasi coppia di punti interni al poligono è tutto all’interno del poligono. Se succede per tutti i punti del poligono, allora il poligono è convesso.
Un poligono è concavo se almeno uno dei suoi angoli interni è concavo, cioè se c’è almeno un lato i cui prolungamenti passano all’interno del poligono. Possiamo riconoscere un poligono concavo tracciando le sue diagonali: almeno una diagonale è esterna al poligono. Anche in questo caso esiste un altro metodo: se troviamo almeno due punti interni al poligono tali che il segmento che li congiunge passa anche all’esterno del poligono, allora il poligono è concavo.
Poligoni equilateri, equiangoli, regolari
Sempre più lati!

Esagoni e dove trovarli
Come fare un pentagono
I poligoni sono delimitati da linee spezzate chiuse, non intrecciate.
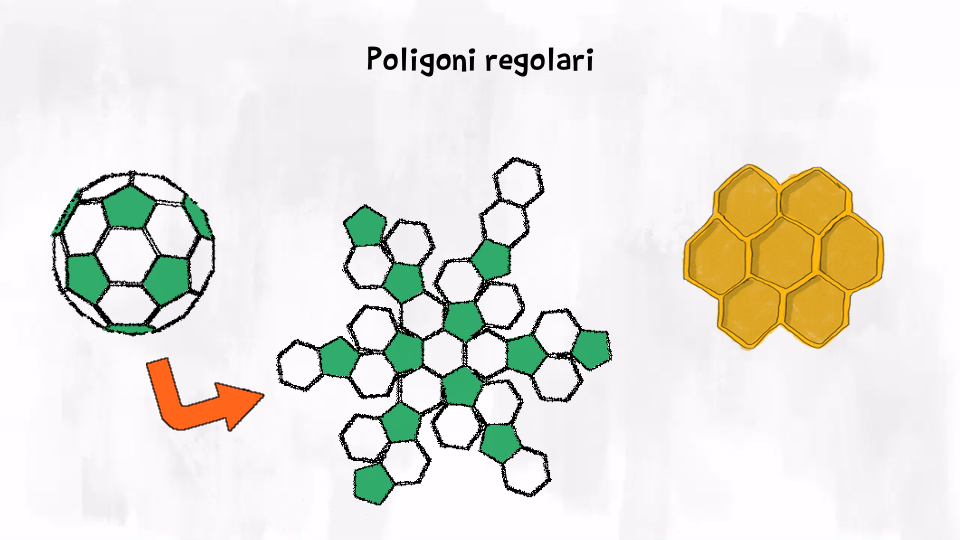
Esistono dei poligoni particolari che hanno tutti i lati uguali: sono i poligoni equilateri. Ci sono altri poligoni che invece hanno tutti gli angoli uguali: sono i poligoni equiangoli. I poligoni che sono sia equilateri sia equiangoli sono i poligoni regolari.
I poligoni regolari hanno tutte le carte in regola: hanno tutti i lati uguali, tutti gli angoli uguali e sono sempre convessi (cioè contengono tutte le loro diagonali); inoltre le diagonali di un poligono regolare sono tutte congruenti tra loro.
I poligoni che non hanno alcuna di queste proprietà sono poligoni irregolari. Questi possono essere sia convessi che concavi. Conosciamo i triangoli regolari (cioè i triangoli equilateri), i quadrilateri regolari (cioè il quadrato), i pentagoni regolari, gli esagoni regolari… Questi ultimi due li ritroviamo anche… Nel pallone! Le toppe del pallone sono pentagoni ed esagoni, così che si possano congiungere a formare una forma sferica. Infatti per costruire il nostro pallone, possiamo utilizzare esagoni e pentagoni regolari, esattamente 12 pentagoni e 20 esagoni. Sono esagoni regolari anche le cellette degli alveari delle api.
Ma più aumentiamo il numero di lati, più questi saranno corti. Un poligono regolare con infiniti lati è una circonferenza: non riusciamo più a distinguere i lati, ma solo una linea curva chiusa. La circonferenza è l’insieme di punti che hanno tutti la stessa distanza da un punto fisso detto centro.
Perimetro di un poligono
La parola perimetro deriva dal greco perimetros e significa “misura intorno". Infatti il perimetro è la misura del contorno di una figura piana.
Se abbiamo un righello, ci basta misurare la lunghezza di tutti i lati del nostro poligono e sommare tutte queste misure. Il risultato che otteniamo è il perimetro del poligono. Infatti misuriamo il perimetro in centrimetri, decimetri, metri… Indichiamo il perimetro con la lettera £$ p $£. Nel caso di un poligono equilatero o un poligono regolare, quindi con tutti i lati uguali, calcolare la lunghezza del perimetro è facile! Basta moltiplicare la lunghezza del lato per il numero di lati del poligono: un poligono regolare di £$ 7 $£ lati di lunghezza £$ \ell $£ avrà perimetro £$ p = 7 \cdot \ell $£.
A cosa serve calcolare il perimetro di un poligono? Può essere utile conoscere la misura del contorno di qualcosa: per incorniciare un quadro, oppure per delimitare la scena del crimine!
