Grafico, simmetrie ed eccentricità di un'ellisse

Agostino Sapienza

INSEGNANTE DI MATEMATICA

Sono nato a Reggio Calabria il 07/10/85. Mi sono diplomato nel 2005 all'Istituto Magistrale Statale Tommaso Gulli. Ho conseguito la laurea triennale in Relazioni Internazionali a Messina e in Economia Internazionale a Padova. Dopo un pò di anni negli studi commercialisti sono stato chiamato per una supplenza covid nella classe di insegnamento A47. Ho poi conseguito l'abilitazione a Trieste nel sostegno e sono entrato di ruolo nel 2023

Scopri le simmetrie dell’ellisse e le sue intersezioni con gli assi. Impara che cosa è l’eccentricità e come si passa dall’equazione al grafico e viceversa.

L’ellisse può avere i fuochi sull’asse £$x$£ oppure sull’asse £$y$£. In ogni caso l’ellisse ha delle caratteristiche particolari, come la simmetria dei suoi punti rispetto agli assi cartesiani oppure rispetto all‘origine.

Dall’equazione si può capire come disegnare l’ellisse: è sempre contenuta in un rettangolo che ha le dimensioni uguali alla misura degli assi dell’ellisse. Inoltre l’eccentricità di un’ellisse è un numero che ci dice quanto un’ellisse è schiacciata sugli assi cartesiani: più è grande l’eccentricità, più l’ellisse è schiacciata su uno dei due assi, più è piccola, più somiglia ad un cerchio.

Simmetrie di un'ellisse e intersezioni con gli assi
Dall'equazione al grafico di un'ellisse
Eccentricità dell'ellisse
Ripassa per l'interrogazione sull'ellisse
Sfida sul grafico dell'ellisse

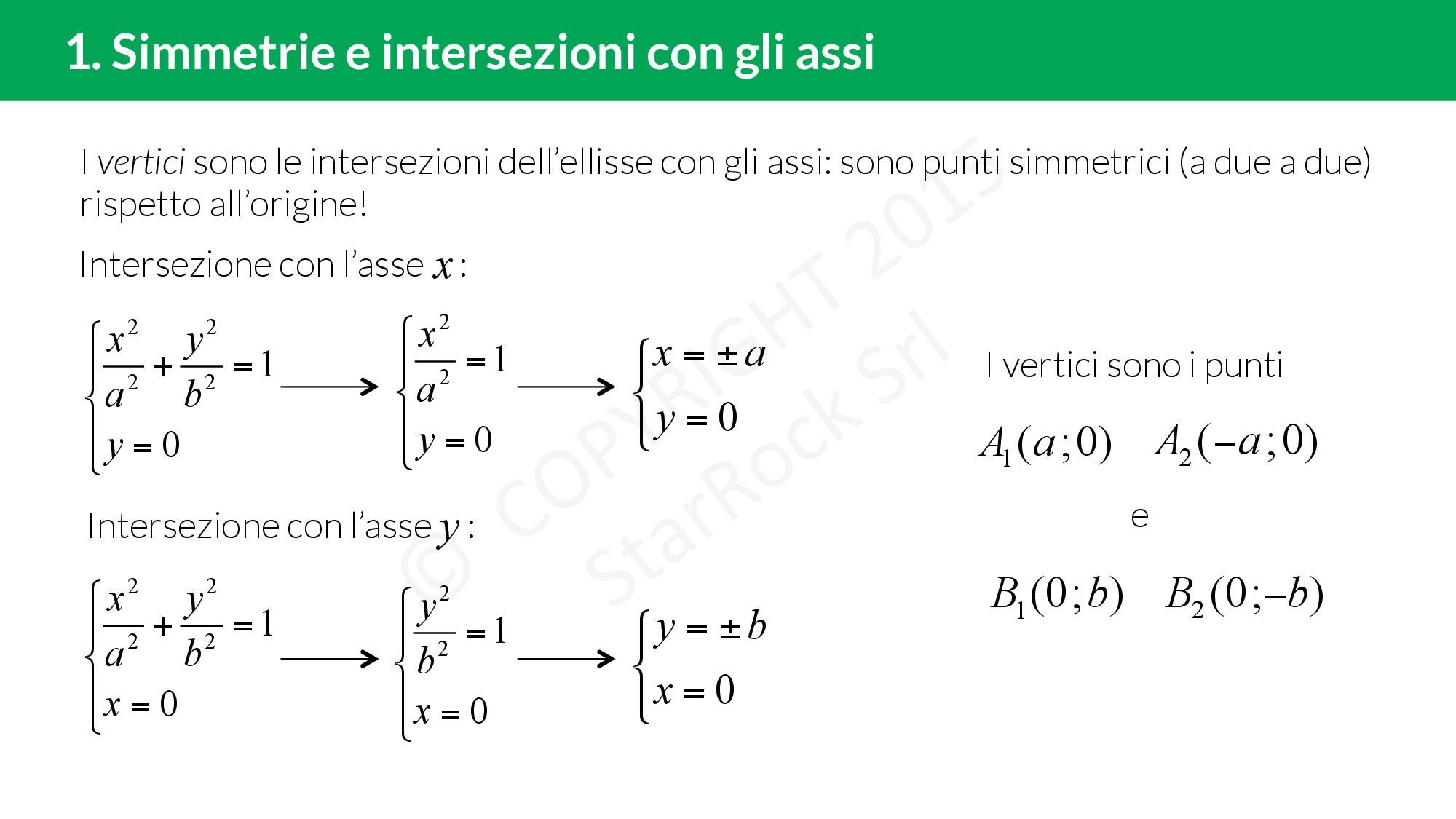
Simmetrie di un’ellisse e intersezioni con gli assi

Data un’ellisse di equazione £$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$£ e un punto £$P(x;y)$£ dell’ellisse, allora:

£$P(x;-y)$£ appartiene ancora all’ellisse ed è simmetrico di £$P$£ rispetto all’asse £$x$£;
£$P(-x;y)$£ appartiene all’ellisse ed è simmetrico di £$P$£ rispetto all’asse £$y$£;
£$P(-x;-y)$£ appartiene all’ellisse ed è simmetrico di £$P$£ rispetto all’origine degli assi £$O$£.

I vertici hanno coordinate £$A_1(a;0)$£, £$A_2(-a;0)$£, £$B_1(0;b)$£ e £$B_2(0;-b)$£. Sono i punti di intersezione dell’ellisse con gli assi e sono simmetrici (a due a due) rispetto all’origine.

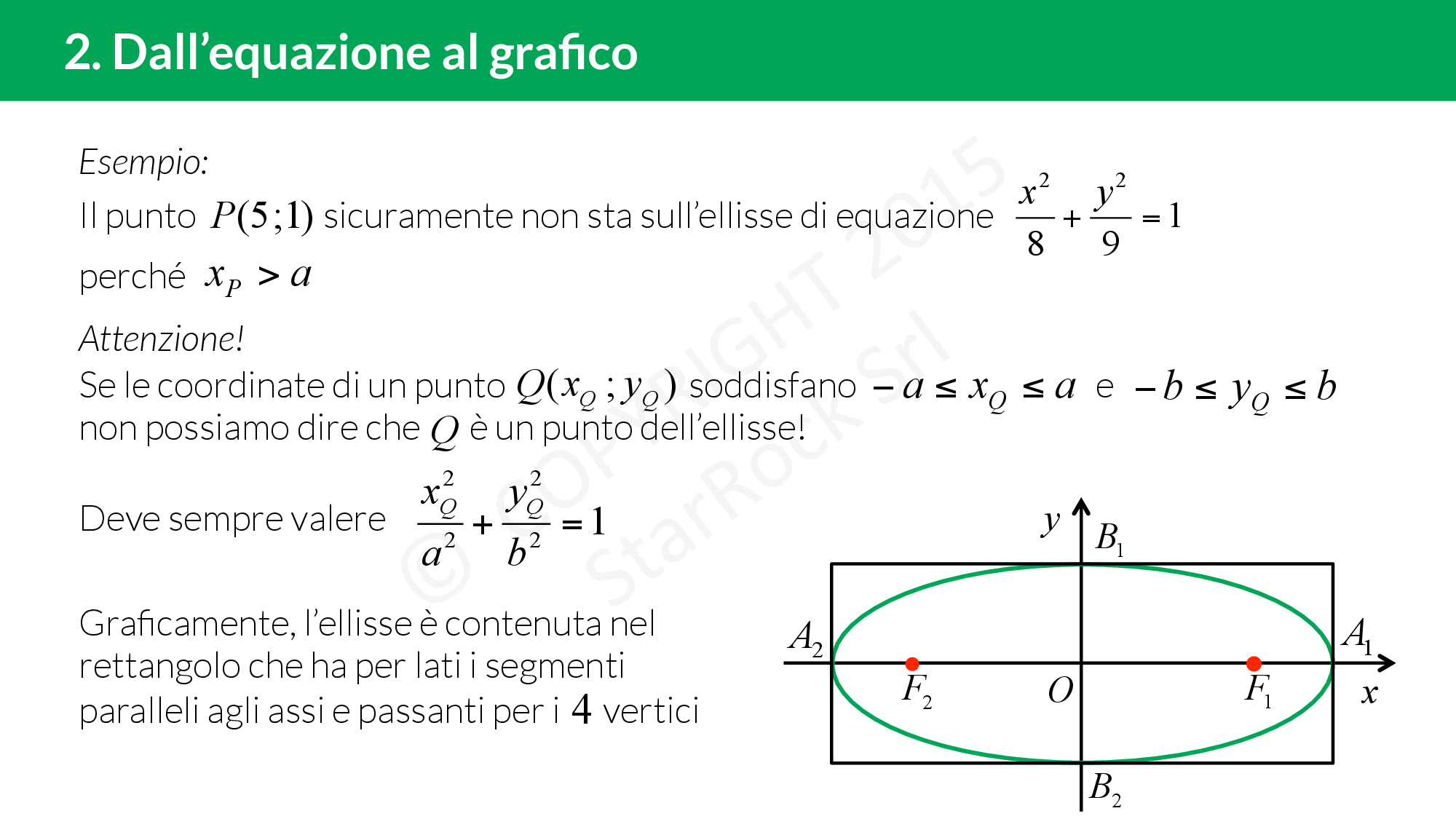
Dall’equazione al grafico di un’ellisse

Data un’ellisse di equazione £$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$£, tutti i suoi punti avranno:

ascissa compresa fra £$-a$£ e £$a$£: £$-a \le x \le a$£
ordinata compresa fra £$-b$£ e £$b$£: £$-b \le x \le b $£

Quindi graficamente, una ellisse è sempre contenuta in un rettangolo di dimensioni £$2a$£ e £$2b$£.

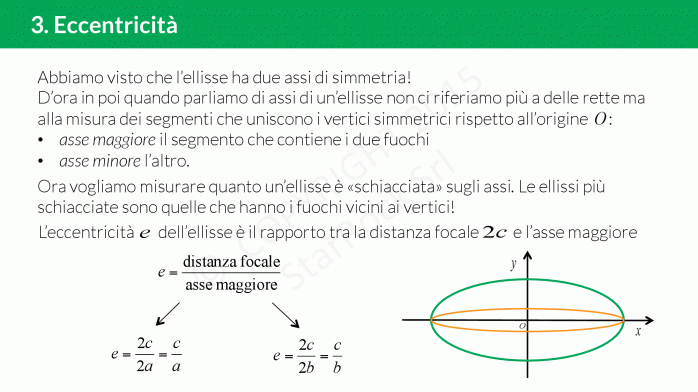
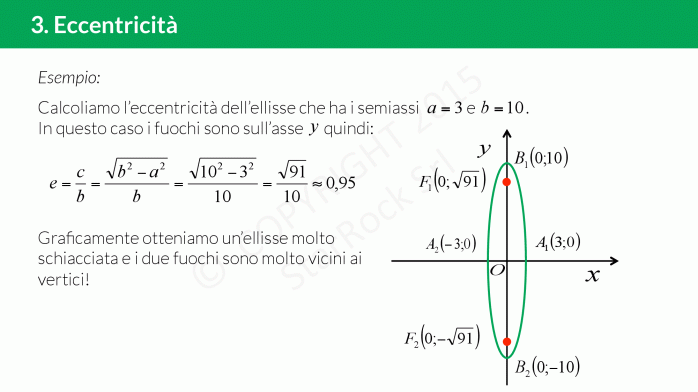
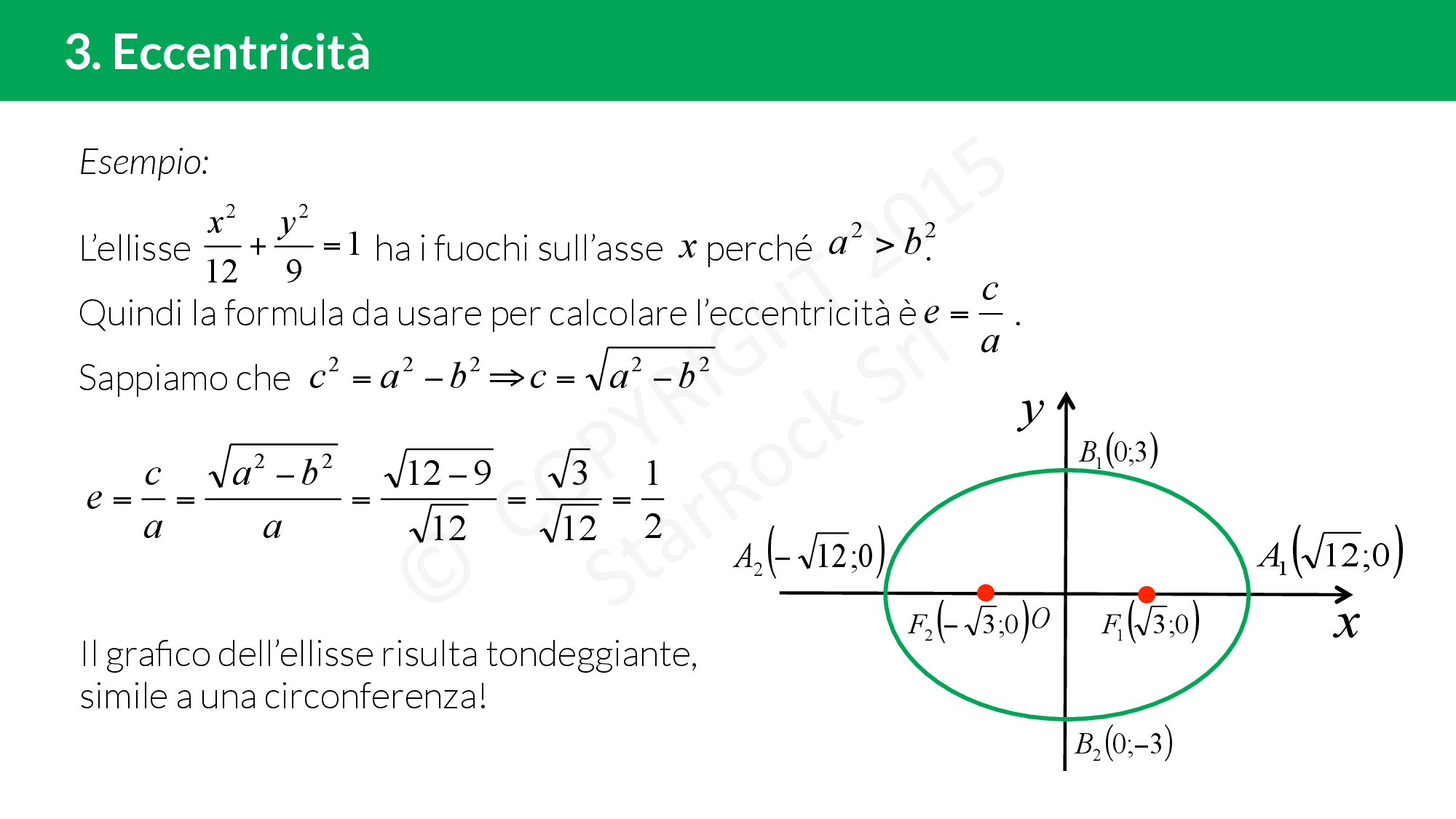
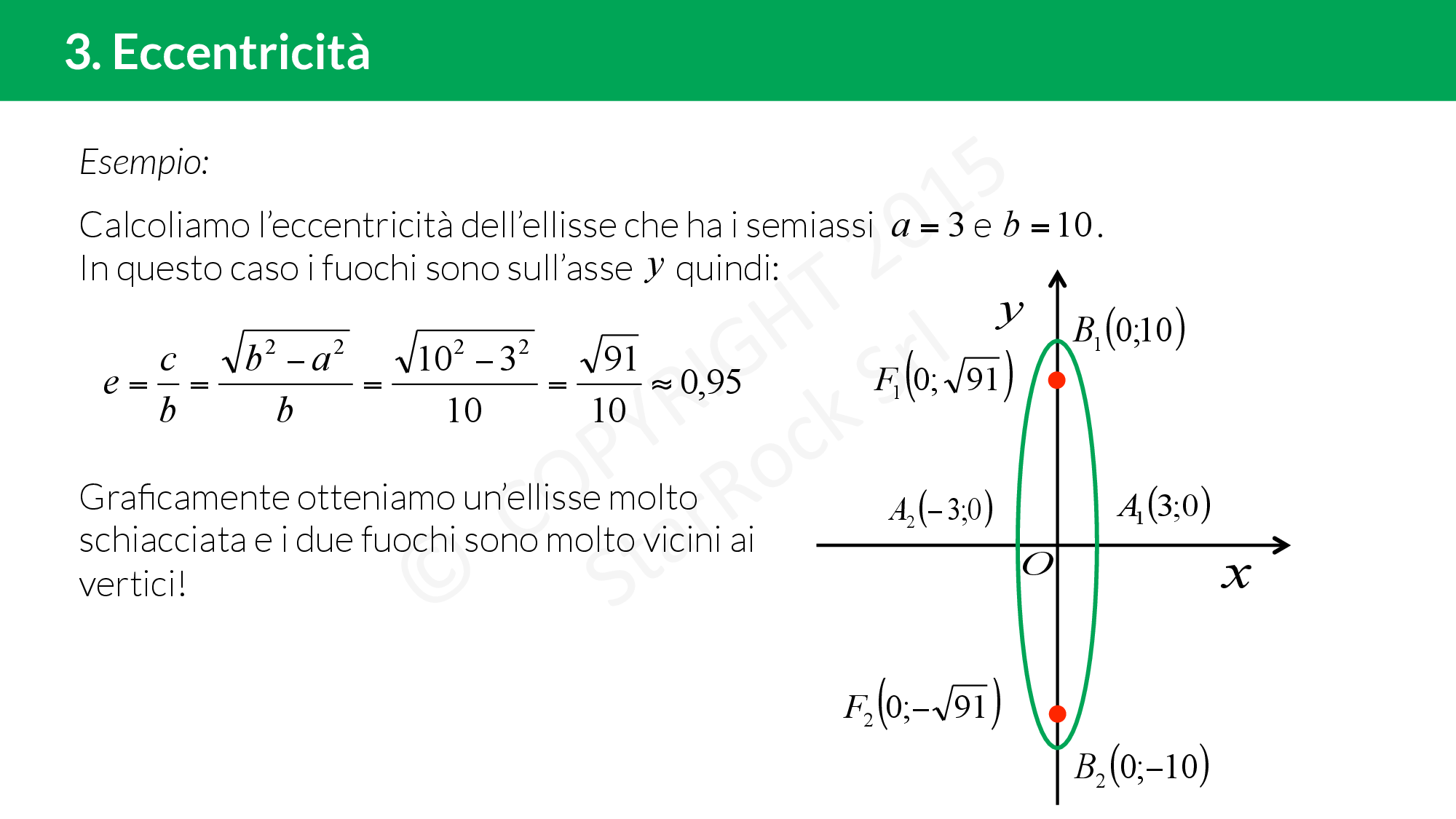
Eccentricità dell’ellisse

L’ellisse ha due assi di simmetria che uniscono i vertici opposti e simmetrici rispetto all’origine. L’asse maggiore è quello che contiene i fuochi, l’asse minore l’altro.

Per misurare quanto l’ellisse è schiacciata su uno degli assi c’è l’eccentricità. L’eccentricità £$e$£ è il rapporto tra la distanza focale £$2c$£ e l’asse maggiore: £$e=\dfrac{distanza \ focale}{asse \ maggiore}$£.

Quindi l’eccentricità è:

£$e=\frac{2c}{2a}=\frac{c}{a}$£ se i fuochi sono sull’asse £$x$£
£$e=\frac{2c}{2b}=\frac{c}{b}$£ se i fuochi sono sull’asse £$y$£

L’eccentricità è un numero sempre compreso fra £$ e [iol_placeholder type="formula" engine="katex" display="inline"]1$£, ma mai uguale a £$1$£: £$ 0 \le e ellisse con eccentricità nulla ha distanza focale nulla, e quindi è una circonferenza.

Se [iol_placeholder type="formula" engine="katex" display="inline"]e=1$£ l’ellisse degenera in un segmento.