Equazione di un'iperbole: come si disegna il grafico

Agostino Sapienza

INSEGNANTE DI MATEMATICA

Sono nato a Reggio Calabria il 07/10/85. Mi sono diplomato nel 2005 all'Istituto Magistrale Statale Tommaso Gulli. Ho conseguito la laurea triennale in Relazioni Internazionali a Messina e in Economia Internazionale a Padova. Dopo un pò di anni negli studi commercialisti sono stato chiamato per una supplenza covid nella classe di insegnamento A47. Ho poi conseguito l'abilitazione a Trieste nel sostegno e sono entrato di ruolo nel 2023

Come per l’ellisse, anche l’iperbole ha delle proprietà e delle caratteristiche che ci permettono di disegnarla più facilmente. Queste caratteristiche sono le simmetrie, la posizione dei vertici, l’intersezione con gli assi e l’eccentricità.

L’iperbole è una curva simmetrica rispetto agli assi cartesiani e anche rispetto all’origine. Le intersezioni tra l’iperbole e gli assi sono i vertici della conica e l‘eccentricità è un numero che dice quanto l’iperbole è aperta.

Passare dal grafico all’equazione e dall’equazione al grafico sarà una passeggiata se leggi attentamente gli esercizi svolti. Ricorda che il grafico delle coniche, se fatto bene, è il primo passo per risolvere bene i problemi di geometria analitica.

Scopriamo insieme come fare.

Iperbole: simmetrie e intersezioni con gli assi
Dall'equazione di un'iperbole al grafico
Eccentricità dell'iperbole
Riassunto sull'equazione dell'iperbole
Esercizi sul grafico dell'iperbole
Sfida sull'iperbole

Iperbole: simmetrie e intersezioni con gli assi

L’iperbole con i fuochi sull’asse £$x$£ ha equazione: £$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$£, quella con i fuochi sull’asse £$y$£, invece, ha equazione £$\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$£.
Qualsiasi siano gli assi su cui si trovano i fuochi, ogni punto £$P$£ dell’iperbole, ha un simmetrico rispetto all’asse £$x$£, rispetto all’asse £$y$£ e rispetto all’origine. Questa proprietà è vera per ogni punto dell’iperbole che quindi è una figura simmetrica rispetto agli assi cartesiani e rispetto all’origine.

Se un’iperbole ha i fuochi sull’asse delle ascisse, allora le intersezioni dell’iperbole con l’asse £$x$£ sono i vertici reali £$A_1(-a;0)$£ e £$A_2(a;0)$£. Non esistono intersezioni reali con l’asse £$y$£, che si chiama asse non trasverso dell’iperbole: i punti £$ B_1(0; -b) $£ e £$ B_2(0; b) $£ sono i vertici non reali dell’iperbole.
Se l’iperbole ha i fuochi sull’asse delle ordinate, l’asse non trasverso è quello delle ascisse, su cui si trovano i vertici non reali. I vertici reali, invece, sono i punti di intersezione fra l’iperbole e l’asse delle £$y$£, cioè £$B_1(0;-b)$£ e £$B_2(0;b)$£.

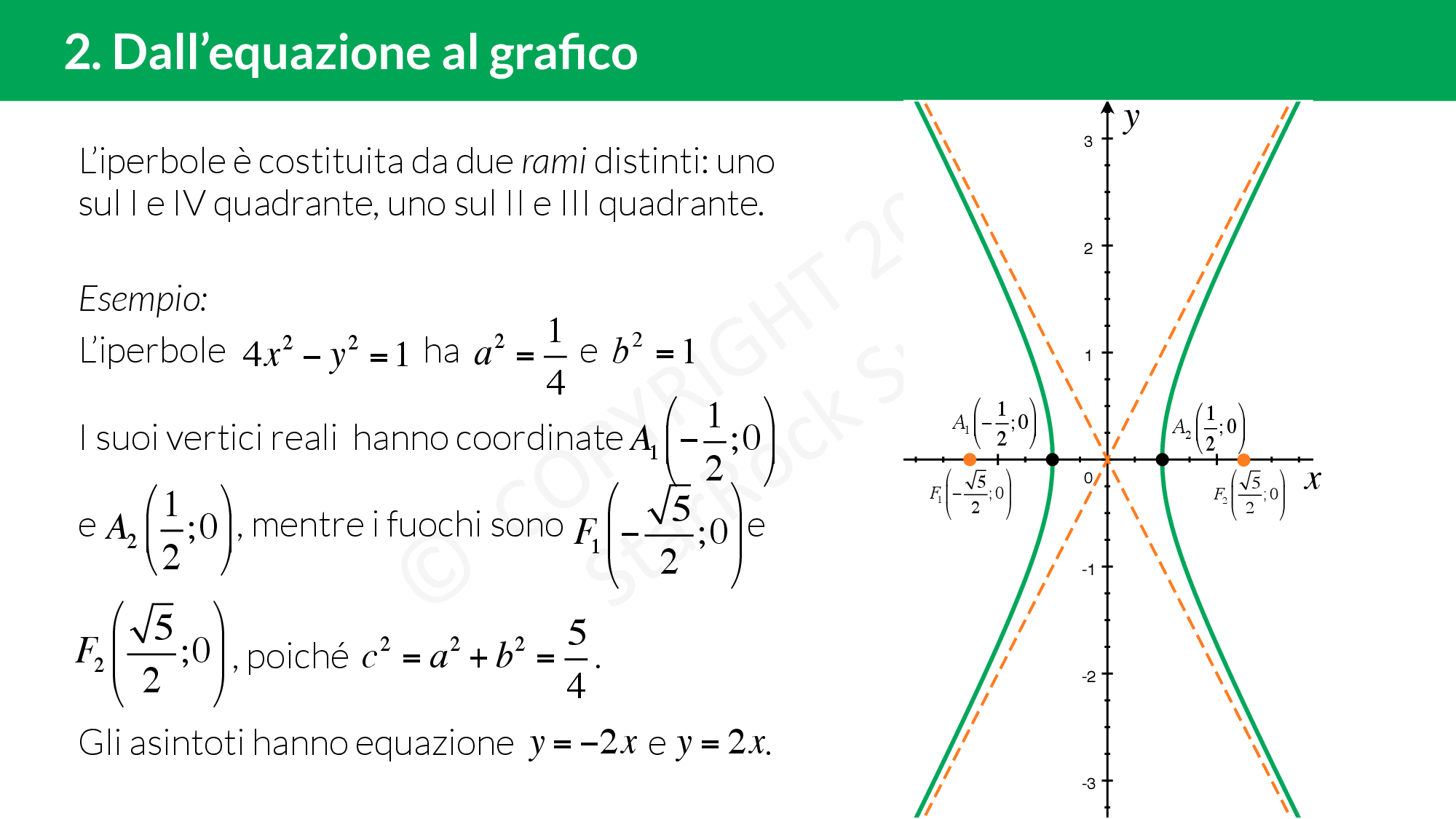
Dall’equazione di un’iperbole al grafico

Disegnare il grafico di un’iperbole è molto facile conoscendo tutte le proprietà dell’iperbole.
Data l’equazione di un’iperbole con i fuochi sull’asse £$x$£, conosciamo i seguenti punti:

vertici reali £$A_1(-a;0)$£ e £$A_2(a;0)$£
vertici non reali £$B_1(0;-b)$£ e £$B_2(0;b)$£
fuochi £$F_1(-c;0)$£, £$F_2(c;0)$£ con £$c= \sqrt{a^2+b^2}$£

Tracciamo le £$4$£ rette parallele agli assi cartesiani e passanti per i vertici e troviamo un rettangolo. Le diagonali prolungate di questo rettangolo sono gli asintoti dell’iperbole. Gli asintoti sono delle rette a cui l’iperbole si avvicina sempre più senza però intersecarle mai. Le equazioni dei due asintoti di un’iperbole con i fuochi sull’asse £$x$£ sono £$y=-\frac{b}{a}x$£ e £$y=\frac{b}{a}x$£

Tutti i punti dell’iperbole, eccetto i vertici non reali, sono esterni al rettangolo appena costruito. Il grafico dell’iperbole è costituito da due rami distinti, che stanno nel I e IV quadrante e nel II e III quadrante rispettivamente. Ogni ramo dell’iperbole assomiglia ad una parabola con vertice in uno dei due vertici reali.

Eccentricità dell’iperbole

L’eccentricità dell’iperbole è un numero che rappresenta la misura dell’apertura dei rami dell’iperbole. In funzione della posizione dei fuochi dell’iperbole possiamo scrivere la formula per trovare l’eccentricità:

£$ e=\frac{c}{a}=\frac{\sqrt{a^2+b^2}}{a}=\sqrt{1+\frac{b^2}{a^2}} $£ per l’iperbole con i fuochi sull’asse £$x$£
£$ e=\frac{c}{b}=\frac{\sqrt{a^2+b^2}}{b}=\sqrt{1+\frac{a^2}{b^2}} $£ per l’iperbole con i fuochi sull’asse £$y$£

L’eccentricità dell’iperbole è un numero sempre maggiore di £$1$£: £$e>1$£. Graficamente, all’aumentare dell’eccentricità aumenta l’apertura dell’iperbole, cioè l’iperbole è più schiacciata sui suoi asintoti.

Riassunto sull’equazione dell’iperbole

Ora che hai visto le prime informazioni sull’iperbole, ti presentiamo una tabella riassuntiva con le formule dell’iperbole con i fuochi sull’asse £$x$£ e con i fuochi sull’asse £$y$£.

Esercizi sul grafico dell’iperbole

Allenati con questi esercizi per verificare quanto hai capito su questa lezione. Ricorda che puoi sempre ripassare sia leggendo le slide che con i tre livelli di esercizi sull’iperbole e il suo grafico!