Iperbole equilatera: definizione e formule
L’iperbole è una particolare conica. Il suo grafico è composto da due rami simmetrici contenuti dentro gli asintoti, rette a cui la figura si avvicina senza toccarle mai.
Un particolare tipo di iperbole è quella equilatera. Nell’equazione dell’iperbole equilatera i due parametri sono uguali, cioè i due assi hanno la stessa lunghezza. Tra le iperboli equilatere ci sono quelle riferite ai propri asintoti, che hanno come asintoti gli assi cartesiani.
Scopri, tramite gli esercizi svolti, i punti particolari e le caratteristiche delle iperboli equilatere! I fuochi, i vertici, gli asintoti, gli assi hanno delle formule più semplici ma puoi ottenerle da quelle dell’iperbole generica.
- Iperbole equilatera riferita agli assi
- Iperbole equilatera riferita agli asintoti
- Rotazione di £$$45°$$£
- Esercizi sull'iperbole
- Sfida su iperbole equilatera
Iperbole equilatera riferita agli assi
Un’iperbole è equilatera quando nell’equazione canonica £$\frac{x^2}{a^2}-\frac{y^2}{b^2}=\pm 1$£ i due parametri sono uguali: £$a^2=b^2$£, cioè quando l’asse trasverso e l’asse non trasverso hanno la stessa lunghezza.
Abbiamo scritto l’equazione con il £$\pm1$£ perché la definizione di iperbole equilatera è valida sia per l’iperbole con fuochi sull’asse £$x$£ che per l’iperbole con i fuochi sull’asse £$y$£.
L’equazione dell’iperbole equilatera diventa:
- £$x^2-y^2=a^2$£ se i fuochi sono sull’asse delle ascisse;
- £$x^2-y^2=-a^2$£ se i fuochi sono sull’asse delle ordinate.
Le caratteristiche delle iperboli equilatere sono molto semplici:
- la coordinata dei fuochi si trova con la stessa formula che abbiamo usato per le iperboli qualsiasi: £$c^2=a^2+b^2 $£, cioè £$c=\pm a \cdot \sqrt{2}$£
- gli asintoti sono le bisettrici dei quadranti, cioè le rette £$y=x$£ e £$y=-x$£
- l’eccentricità ha un valore fisso pari a £$\sqrt{2}$£. La formula dell’eccentricità permette di dimostrare che £$e=\sqrt{2}$£ per le iperboli equilatere.
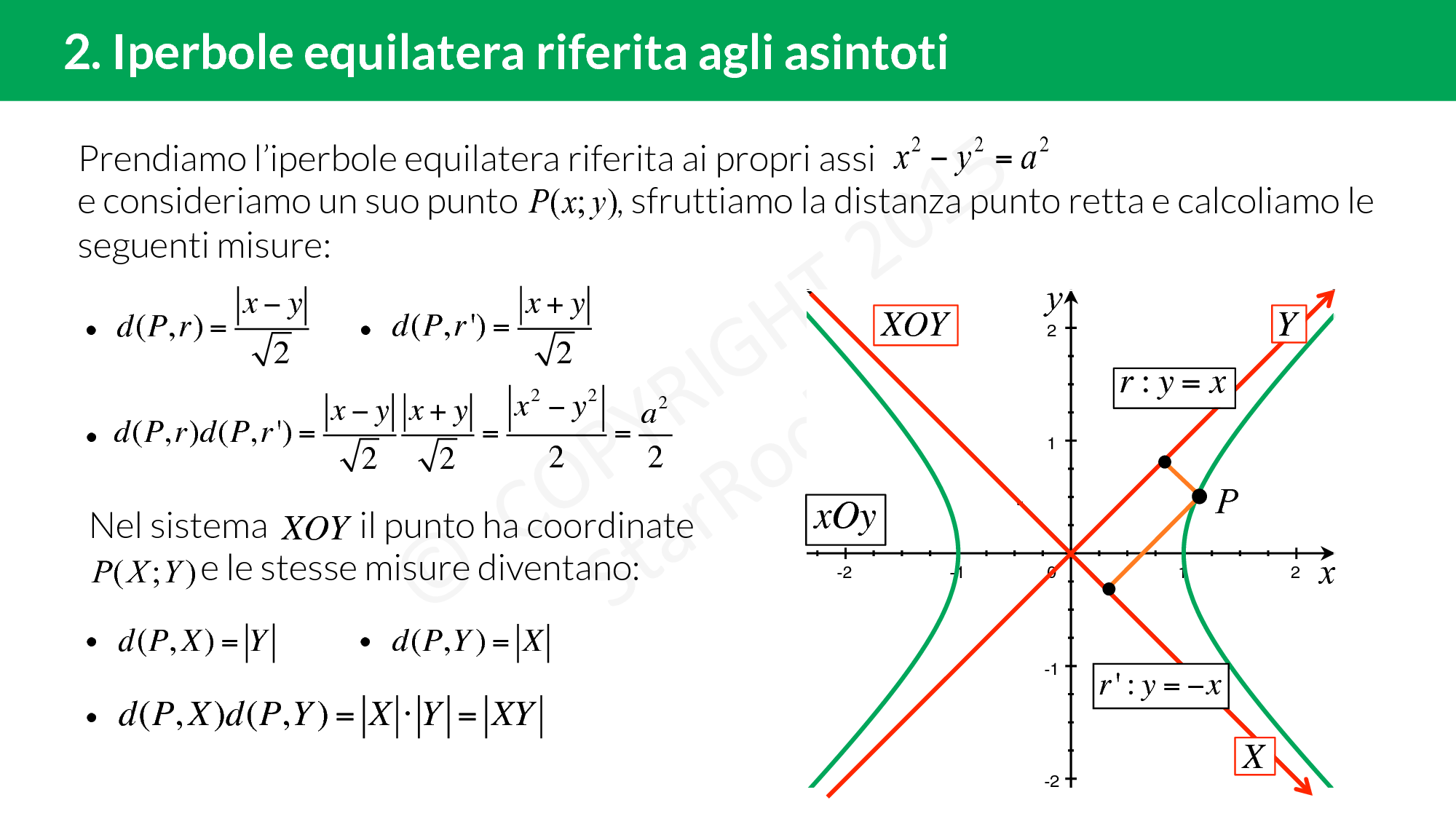
Iperbole equilatera riferita agli asintoti
L’iperbole equilatera riferita ai propri asintoti è un’iperbole equilatera considerata in un nuovo sistema di riferimento in cui gli assi cartesiani sono i suoi asintoti. Gli asintoti di un’iperbole equilatera sono le bisettrici dei quadranti e sono fra loro perpendicolari, quindi possiamo usarle come assi cartesiani per un nuovo sistema di riferimento.
L’iperbole equilatera riferita ai propri asintoti ha equazione £$xy=\pm k$£, dove £$k = \frac{a^2}{2}$£. Al variare del parametro £$k$£ varia la posizione dell’iperbole nel piano cartesiano:
- se £$k > 0$£ i due rami stanno nel I e nel III quadrante;
- se [iol_placeholder type="formula" engine="katex" display="inline"]k
Gli elementi principali dell’iperbole riferita ai propri asintoti:
- gli asintoti sono gli assi cartesiani;
- gli assi di simmetria sono le bisettrici dei quadranti. Quindi i fuochi e i vertici dell’iperbole equilatera riferita ai propri asintoti sono punti delle bisettrici;
- i vertici hanno coordinate:
- se £$k > 0$£: £$A_1 \left(-\sqrt{k}; -\sqrt{k} \right)$£, £$A_2 \left(\sqrt{k}; \sqrt{k} \right)$£
- se [iol_placeholder type="formula" engine="katex" display="inline"]k
- le coordinate dei fuochi sono la metà della distanza focale £$c=2 \sqrt{|k|}$£, quindi le coordinate dei fuochi dell’iperbole equilatera riferita ai propri asintoti sono:
- se £$k > 0$£: £$F_1 \left(-\sqrt{2k}; -\sqrt{2k} \right)$£, £$F_2 \left(\sqrt{2k}; \sqrt{2k} \right)$£
- se [iol_placeholder type="formula" engine="katex" display="inline"]k
- l’asse trasverso ha lunghezza £$2a=2\sqrt{2|k|}$£
Rotazione di £$$45°$$£
Possiamo trovare l’iperbole riferita ai propri asintoti anche come rotazione di £$45°$£ dell’iperbole equilatera riferita agli assi.
La rotazione è un’isometria, quindi conserva le distanze, per questo motivo le due iperboli avranno le stesse caratteristiche.
Esercizi sull’iperbole

Hai visto che ci sono tanti tipi di iperbole: quale scegliere? E poi, come si disegnano?
Per rispondere a queste domande, allenati e preparati all’interrogazione con questi esercizi e con quelli che trovi nei tre livelli!
Sfida su iperbole equilatera
Testo e soluzione:
Sei ancora sull’half-pipe! Ma quando scenderai? Prova a risolvere la sfida mentre sei su, ma attento a non farti male!