Posizioni reciproche delle circonferenze: tangenti e concentriche
Nel mondo della geometria ci sono moltissime interazioni tra le forme geometriche e oggi analizzeremo come possono interfacciarsi tra di loro due circonferenze. Come si rapportano tra loro? In quali modi possono interagire?
Immaginiamo di avere due circonferenze, ognuna definita dal proprio centro e raggio. Quali possono essere le loro posizioni reciproche? In alcuni casi, potrebbero non avere alcun punto in comune, mentre in altri potrebbero intersecarsi in uno o due punti. Inoltre, possono essere tangenti o concentriche. Le circonferenze tangenti toccano solo in un punto, mentre le circonferenze concentriche condividono lo stesso centro.
In quest’articolo, analizzeremo in dettaglio questi due casi, spiegando come si possano riconoscere e come possano essere descritte matematicamente. Pronti? Iniziamo!
- La posizione reciproca di due circonferenze: quando sono tangenti
- La posizione reciproca di due circonferenze: quando sono concentriche
- Interrogazione sulla posizione reciproca di due circonferenze: le possibili domande
La posizione reciproca di due circonferenze: quando sono tangenti
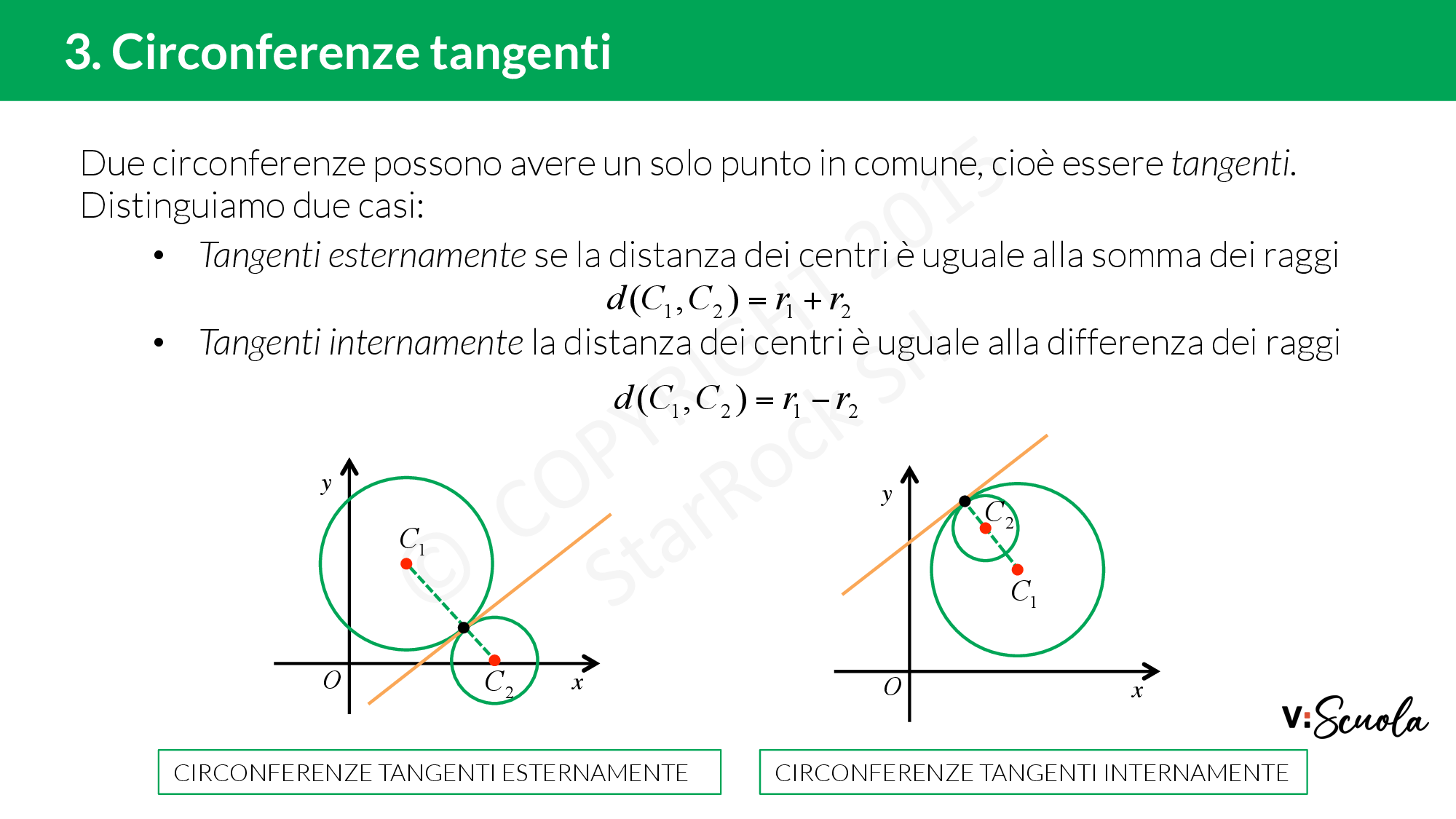
Due circonferenze possono avere un solo punto in comune, cioè essere tangenti. In questo scenario, due circonferenze si toccano in un solo punto e ciò significa che i loro bordi si intersecano in una singola posizione, ma non si sovrappongono.
Distinguiamo due casi:
- Tangenti esternamente se la distanza dei centri è uguale alla somma dei raggi. Nel caso esterno, i centri delle due circonferenze si trovano su due lati opposti del punto di tangenza;
- Tangenti internamente la distanza dei centri è uguale alla differenza dei raggi. Nel caso interno, invece, una delle circonferenze è completamente contenuta nell’altra, e i loro centri sono allineati con il punto di tangenza.
L’asse radicale in questo caso è la retta tangente comune alle due circonferenze. Il punto di tangenza è chiamato punto base.
Attenzione! Possiamo trovare l’equazione dell’asse radicale e le coordinate del punto base con lo stesso procedimento usato per trovare i punti di intersezione di due circonferenze secanti!
La posizione reciproca di due circonferenze: quando sono concentriche
Due circonferenze sono concentriche se i loro centri coincidono:
Quindi due circonferenze sono concentriche se il coefficiente di £$x$£ della prima circonferenza è uguale al coefficiente di £$x$£ della seconda e il coefficiente di £$y$£ della prima circonferenza è uguale al coefficiente di £$y$£ della seconda.
Questo significa che se tracciassimo linee dal centro di queste circonferenze a qualsiasi punto sui loro bordi, otterremmo raggi di diverse lunghezze per ogni circonferenza. Queste circonferenze non si intersecano, ma piuttosto creano una serie di anelli concentrici, come in un bersaglio o in una cipolla.
Interrogazione sulla posizione reciproca di due circonferenze: le possibili domande

Sei pronto per l’interrogazione? Prova a rispondere a queste domande.
Se hai dubbi, riguarda la lezione e allenati con gli esercizi!