Integrali definiti e indefiniti: definizioni ed esempi
Gli integrali sono uno strumento fondamentale nella matematica che ci aiuta a capire e a calcolare le aree, i volumi e altri concetti che coinvolgono l’accumulazione o la somma di quantità infinite.
Ci sono due tipi principali di integrali che studiamo: gli integrali definiti e gli integrali indefiniti, ognuno con il proprio ruolo e applicazione. Gli integrali indefiniti sono come una parte generale della soluzione a un problema. Quando integriamo in modo indefinito, stiamo cercando una funzione che, quando derivata, ci dà la funzione originale con cui abbiamo iniziato.
D’altra parte, gli integrali definiti sono molto specifici. Li usiamo quando vogliamo calcolare l’area sotto una curva tra due punti specifici su un grafico. È come misurare esattamente un pezzo di terreno tra due paletti.
Questo articolo esplorerà più a fondo questi due concetti, spiegando come si calcolano, quali sono le loro differenze e come possono essere applicati in vari contesti pratici.
- Tabella delle formule per integrare le funzioni elementari
- Cosa sono gli integrali
- Integrale definito
- Integrali indefiniti
- Integrali indefiniti: integrazione delle funzioni elementari
- Esercizi sugli integrali
Tabella delle formule per integrare le funzioni elementari
Riassumiamo in una tabella le formule per integrare le funzioni elementari, cioè le formule dell’integrale delle:
- funzioni potenza,
- funzioni esponenziali,
- funzioni logaritmiche,
- del seno, del coseno, della tangente e della cotangente.
Cosa sono gli integrali
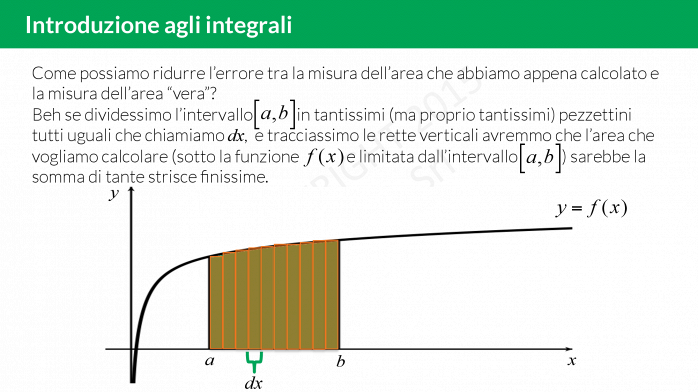
Introduzione agli integrali
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
Un po’ di storia degli integrali
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
Il calcolo degli integrali è considerato da molti studenti un argomento difficile. Ma, come tutti, lo diventa se non si capisce il motivo per cui vanno studiati. Abbiamo pensato quindi di presentare una breve introduzione agli integrali e anche un po’ di storia (che male non fa).
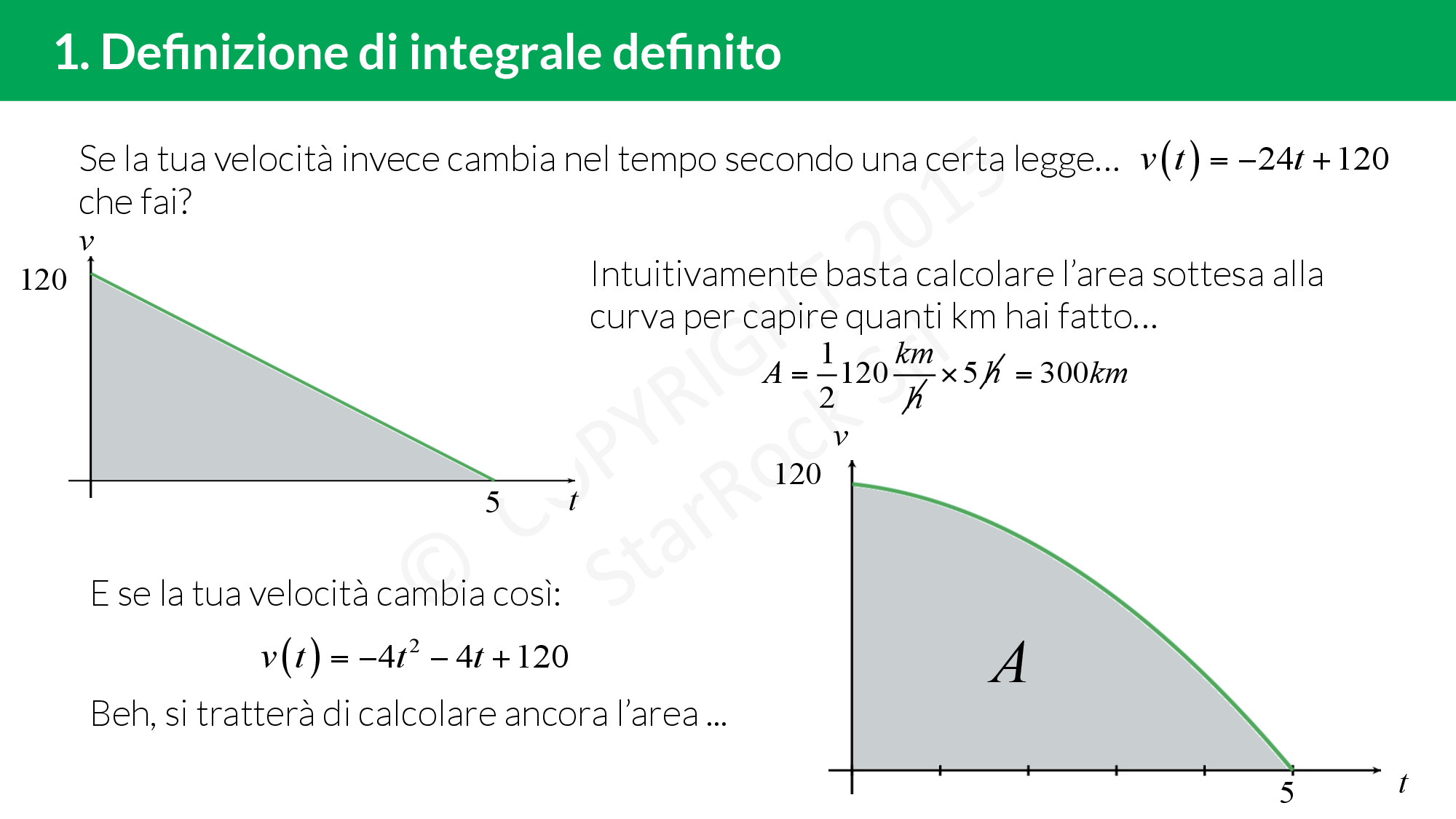
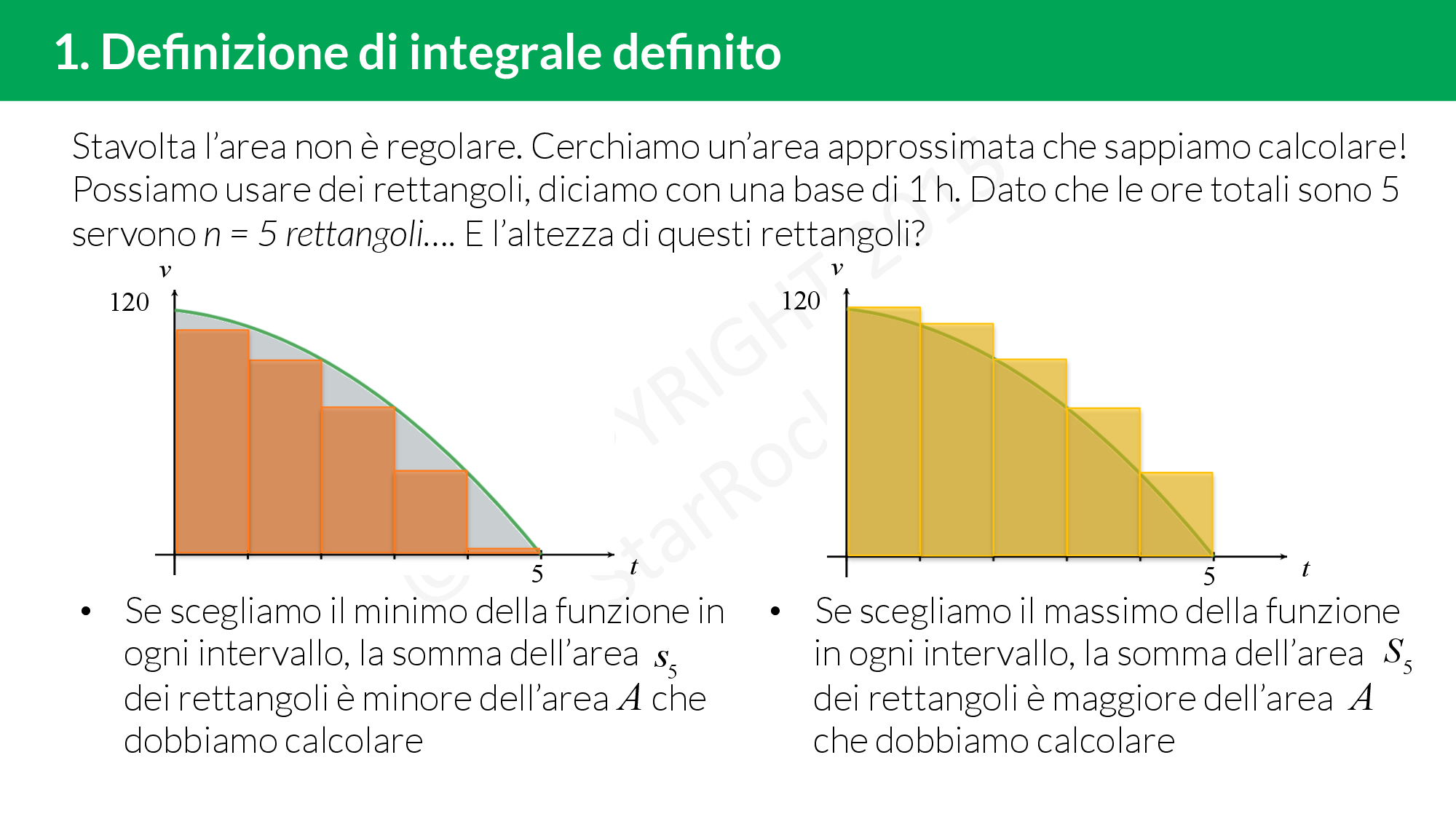
Integrale definito
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
L’integrale definito di una funzione è scritto come $$\int_a^b f(x) dx $$ ed è uguale ad un numero.
Usi l’integrale definito quando:
- devi calcolare un’area non regolare (quando i bordi sono curve);
- devi risolvere equazioni differenziali.
Integrali indefiniti
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
L’integrale indefinito di una funzione è un insieme di funzioni. È l’insieme di tutte le funzioni primitive. Quindi se £$\int f(x) dx = G(x) + c $£ con £$c$£ costante, £$G(x) + c$£ è l’insieme delle funzioni primitive.
Una funzione primitiva è quella che ha come derivata la funzione che vogliamo integrare. Quindi la funzione £$G(x)$£ è la primitiva di £$f(x)$£ se £$G'(x)=f(x)$£.
Userai l’integrale indefinito per calcolare gli integrali definiti.
Integrali indefiniti: integrazione delle funzioni elementari
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
Come calcolare gli integrali indefiniti? Per molte funzioni è facile!
Infatti ti basta sapere che “l’integrale è l’inverso della derivata“. Cioè se abbiamo la funzione £$f(x)=x^2$£, il suo integrale indefinito è quella funzione che ha £$f$£ come derivata. Ma se per derivare questa funzione (potenza) abbassavamo di uno il grado, per tornare indietro dobbiamo aggiungere uno. Quindi avremo £$F(x)=x^3$£. Ma siamo sicuri di aver fatto giusto? Proviamo: $$F'(x)=3x^2 \ne f(x)$$
Manca un coefficiente (£$3$£). Allora la primitiva corretta è quella che ha £$3$£ al denominatore perché derivando possiamo semplificare. Avremo £$F(x)=\frac{x^3}{3}$£. Ma ce n’è solo una? No! Ce ne sono infinite: dato che la derivata di una costante è nulla, anche tutte le funzioni £$G(x)=\frac{x^3}{3}+c$£ con £$c$£ numero reale hanno come derivata £$f(x)=x^2$£.
Esercizi sugli integrali
Testo degli esercizi
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
Soluzione degli esercizi
Integrali definiti e integrali indefiniti: definizioni ed esempi - Galleria
Ora che sei entrato nel magico mondo degli integrali, prova a risolvere questi esercizi su integrali definiti e indefiniti.
Trovi tanti altri esercizi nei tre livelli. Allenati per diventare cintura nera nel calcolo degli integrali!